능지처참을 느낍니다...

문제 링크

---

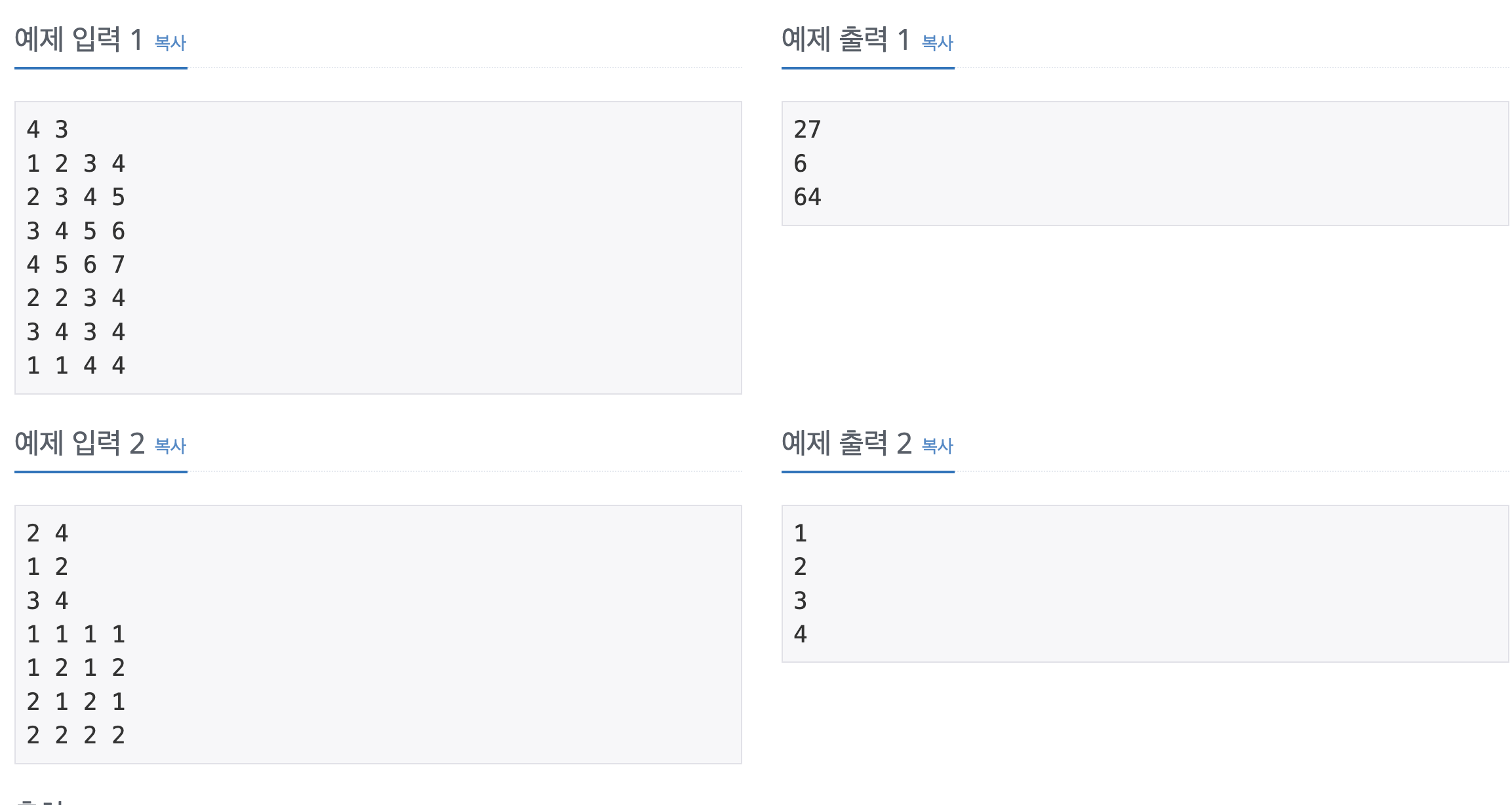
아이디어 및 코드

1. 누적합(PrefixSum) 구해놓고 풀어야 하는 문제
2. 좀 단순하게 생각했다. 어쨌든 풀긴 풀었음

public static class BOJ11660 {
        public static void main(String[] args) throws IOException {
            BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
            StringTokenizer st = new StringTokenizer(br.readLine());

            int N = Integer.parseInt(st.nextToken()); // 표의 크기
            int M = Integer.parseInt(st.nextToken()); // 합의 구해야 하는 횟수

            int[][] map = new int[N + 1][N + 1]; // 0번인덱스 걍 제외

            for (int i = 1; i <= N; i++) {
                st = new StringTokenizer(br.readLine());
                for (int j = 1; j <= N; j++) {
                    map[i][j] = Integer.parseInt(st.nextToken());
                }
            }

            int[][] prefixMap = new int[N + 1][N + 1];

            for (int i = 1; i < map.length; i++) {
                for (int j = 1; j < map.length; j++) {
                    prefixMap[i][j] = prefixMap[i][j - 1] + map[i][j]; // 누적합 이중배열, column 마다 초기화된다
                }
            }

            int[] answer = new int[M];

            for (int i = 0; i < M; i++) {
                int sum = 0;
                st = new StringTokenizer(br.readLine());
                int x1 = Integer.parseInt(st.nextToken());
                int y1 = Integer.parseInt(st.nextToken());
                int x2 = Integer.parseInt(st.nextToken());
                int y2 = Integer.parseInt(st.nextToken());

                // [2,2] , [3,4] 라고 한다면 -> 2,1 빼야하고, 3,1 빼야함 즉

                // 5 * 5 배열에서, 2,2 부터 4, 4 라고 한다면../

                // x2의 시작점은 x1 으로 고정된다 ( 행의 계산은 이만큼만 한다)
                // y2의 시작점은 y1 으로 고정된다 ( 열의 계산은 이만큼만 한다)

                // 따라서, [2,2] ~ [3,4] 뭐 이런식으로 한다면 2 (y1) 이전의 값들을 매 반복마다 빼줘야하고...
                // y의 길이만큼 반복해줘야 한다. (x2 - x1) 의 길이만큼

                for (int j = x1; j <= x2; j++) {
                    // 2라면 1번 인덱스 죽여버리면 됨 (y 기준)
                    sum += prefixMap[j][y2] - prefixMap[j][y1 - 1]; //
                }

                answer[i] = sum;
            }

            for (int i : answer) {
                System.out.println(i);
            }
        }


    }

해설 (입력부 제외)

            for (int i = 1; i < map.length; i++) {
                for (int j = 1; j < map.length; j++) {
                    prefixMap[i][j] = prefixMap[i][j - 1] + map[i][j]; // 누적합 이중배열, column 마다 초기화된다
                }
            }

여기서 누적합의 초기화를 하는데, 실질적으로 나타나는 형태는 다음과 같다.

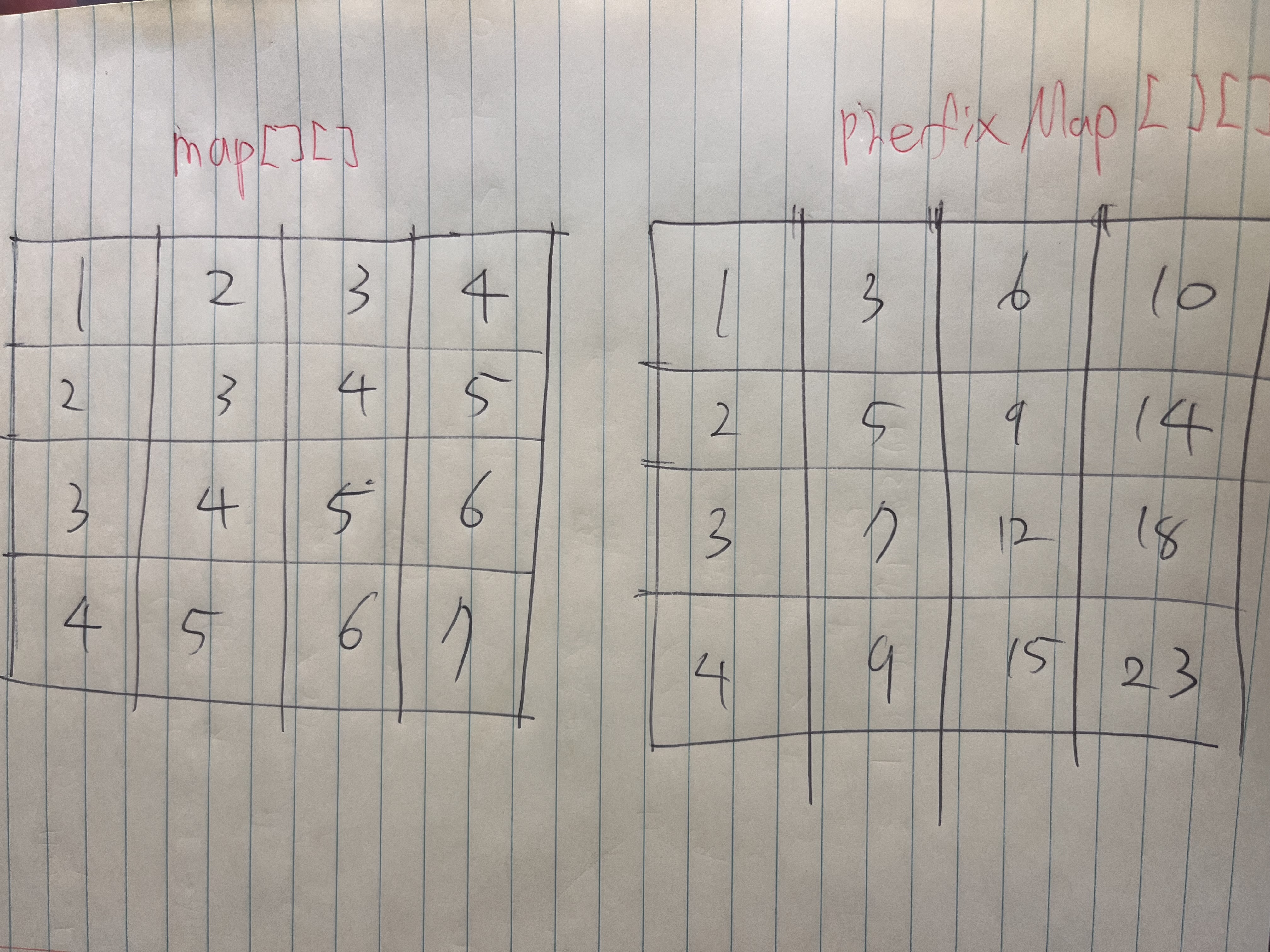
좌측이 map, 오른쪽이 누적합 선언한 prefixMap

그래서 만약, {2 2 3 4} 입력을 받았다면 (2,2) 부터 (3,4) 부분을 찾게 되는데, 그림은 아래와 같다

위와 같은 형태. 그러므로 합 계산을 할 때, 입력값 {x1, y1, x2, y2} 기준으로

1. 유효한 row들 기준으로 (x1 ~ x2)
2. prefix[y2] - prefix[y1 - 1] 값 (유효한 범위)

for (int i = 0; i < M; i++) {
                int sum = 0;
                st = new StringTokenizer(br.readLine());
                int x1 = Integer.parseInt(st.nextToken());
                int y1 = Integer.parseInt(st.nextToken());
                int x2 = Integer.parseInt(st.nextToken());
                int y2 = Integer.parseInt(st.nextToken());

                // [2,2] , [3,4] 라고 한다면 -> 2,1 빼야하고, 3,1 빼야함 즉

                // 5 * 5 배열에서, 2,2 부터 4, 4 라고 한다면../

                // x2의 시작점은 x1 으로 고정된다 ( 행의 계산은 이만큼만 한다)
                // y2의 시작점은 y1 으로 고정된다 ( 열의 계산은 이만큼만 한다)

                // 따라서, [2,2] ~ [3,4] 뭐 이런식으로 한다면 2 (y1) 이전의 값들을 매 반복마다 빼줘야하고...
                // y의 길이만큼 반복해줘야 한다. (x2 - x1) 의 길이만큼

                for (int j = x1; j <= x2; j++) {
                    // 2라면 1번 인덱스 죽여버리면 됨 (y 기준)
                    sum += prefixMap[j][y2] - prefixMap[j][y1 - 1]; //
                }

                answer[i] = sum;
            }

• 주저리 주저리 해놨지만, 결국 색칠한 범위를 찾아서 계산해주는 것.
• 성능은 좋지 않다