병합 정렬(with 움짤+Java) - MergeSort
병합정렬 움짤
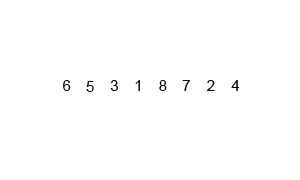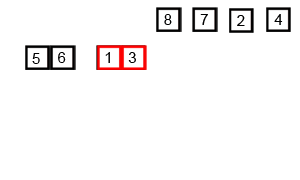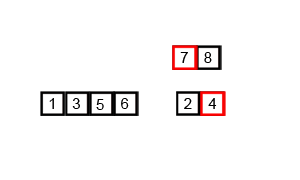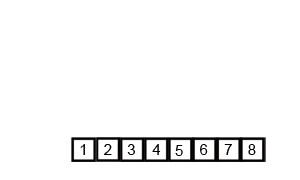
자바 코드
전체코드
public class MergeSort {
public static void main(String[] args) {
int[] arr = { 29, 10, 14, 37, 13 };
mergeSort(arr, 0, arr.length - 1);
for (int i : arr) {
System.out.print(i + " ");
}
}
public static void mergeSort(int[] arr, int left, int right) {
if (left < right) {
int mid = (left + right) / 2;
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
merge(arr, left, mid, right);
}
}
public static void merge(int[] arr, int left, int mid, int right) {
int[] temp = new int[arr.length];
int i = left;
int j = mid + 1;
int k = left;
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
temp[k++] = arr[i++];
} else {
temp[k++] = arr[j++];
}
}
while (i <= mid) {
temp[k++] = arr[i++];
}
while (j <= right) {
temp[k++] = arr[j++];
}
for (int index = left; index < k; index++) {
arr[index] = temp[index];
}
}
}
1. Divide
public static void mergeSort(int[] arr, int left, int right) {
if (left < right) {
int mid = (left + right) / 2;
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
merge(arr, left, mid, right);
}
}설명
public static void mergeSort(int[] arr, int left, int right)함수의 매개변수 : 정렬할 배열(arr)과 배열의 시작 인덱스(left)와 끝 인덱스(right)
if (left < right) 함수의 시작 부분에서는 배열을 반으로 나누기 위한 조건을 확인
- 배열의 크기가 1보다 작거나 같으면 이미 정렬된 상태이므로 정렬할 필요가 없다.
int mid = (left + right) / 2;배열의 중간 인덱스(mid)를 계산
- 배열을 반으로 나누기 위해서는 배열의 시작 인덱스(left)와 끝 인덱스(right)의 합을 2로 나눈다
mergeSort(arr, left, mid);배열의 왼쪽 부분을 정렬하기 위해 mergeSort() 함수를 재귀적으로 호출
- 이때, 시작 인덱스는 left로 유지하고, 끝 인덱스는 mid로 설정
mergeSort(arr, mid + 1, right);배열의 오른쪽 부분을 정렬하기 위해 mergeSort() 함수를 재귀적으로 호출
- 이때, 시작 인덱스는 mid+1로 설정하고, 끝 인덱스는 right로 유지
merge(arr, left, mid, right);왼쪽과 오른쪽 부분을 정렬한 후, 두 부분을 병합
2. Conquer
public static void merge(int[] arr, int left, int mid, int right) {
int[] temp = new int[arr.length];
int i = left;
int j = mid + 1;
int k = left;
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
temp[k++] = arr[i++];
} else {
temp[k++] = arr[j++];
}
}
while (i <= mid) {
temp[k++] = arr[i++];
}
while (j <= right) {
temp[k++] = arr[j++];
}
for (int index = left; index < k; index++) {
arr[index] = temp[index];
}
}머지하는 부분
설명
int[] temp = new int[arr.length];먼저, 정렬된 배열을 저장할 임시 배열 temp를 생성
- 이 배열은 정렬된 배열을 저장하는 데 사용된다.
int i = left;
int j = mid + 1;
int k = left;왼쪽 부분의 시작 인덱스 i, 오른쪽 부분의 시작 인덱스 j, 그리고 정렬된 배열의 시작 인덱스 k를 각각 left, mid+1, left로 초기화
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
temp[k++] = arr[i++];
} else {
temp[k++] = arr[j++];
}
}while 문을 사용하여 왼쪽 부분과 오른쪽 부분의 원소를 비교하고 작은 원소부터 temp 배열에 저장
- i가 mid보다 작거나 같고, j가 right보다 작거나 같을 때까지 반복
while (i <= mid) {
temp[k++] = arr[i++];
}
while (j <= right) {
temp[k++] = arr[j++];
}위의 while문이 종료되면 왼쪽 부분이나 오른쪽 부분 중 하나는 남은 원소가 있을 수 있다.
- 남은 원소들을 while문 사용해서 temp 배열에 저장
for (int index = left; index < k; index++) {
arr[index] = temp[index];
}마지막으로, temp 배열의 값을 arr 배열에 복사
++
나무위키의 설명
성능은 아래의 퀵 정렬보다 전반적으로 뒤떨어지고, 데이터 크기만한 메모리가 더 필요하지만 '최대의 장점은 데이터의 상태에 별 영향을 받지 않는다는 점'이다.
힙이나 퀵의 경우에는 배열 A[25]=100, A[33]=100인 정수형 배열을 정렬한다고 할 때, 33번째에 있던 100이 25번째에 있던 100보다 앞으로 오는 경우가 생길 수 있다.
그에 반해서 병합정렬은 이런 일이 발생하지 않는다. 기본적으로 병합정렬은 쪼갠 후 두 값을 비교할 때 값이 같으면 정렬하지 않게 설계되기 때문이다.
그게 뭐가 중요하냐고 할 수 있지만, 실제 상황에서 여러 기준으로 정렬했을 때 동일 값에 대해선 기존 기준의 정렬순서가 유지되어야 한다.
예를 들어 동점일 경우 생년월일 기준으로 수상자를 뽑는 규정이 있는 대회에서 참가자들을 생년월일 순서대로 정렬해놓고 시험점수 기준으로 다시 정렬할 경우, 병합 정렬은 동점자들끼리 생년월일 순서대로 정렬된 것이 100% 유지된다.
정렬되어 있는 두 배열을 합집합할 때 이 알고리즘의 마지막 단계만을 이용하면 가장 빠르게 정렬된 상태로 합칠 수 있다.
장단점
장점
- O(logN) 의 시간복잡도를 가진다
- 정렬의 순서가 중요한 경우 효율적이다(동일한 값이지만 순서가 중요한경우)
단점
- 추가 배열을 사용하므로 메모리 사용량이 증가한다
- 따라서 메모리 사용량이 중요하거나, 매우 큰 데이터의 경우 비효율적일 수 있다.
