Mixed Precision Training

손기훈·2024년 9월 2일

딥러닝 엔지니어링

목록 보기

5/7

What is Mixed Precision Training?

기존에 신경망을 학습시키는 데에는 대부분 32bit의 실수형 데이터들이 사용되었지만, 32bit의 가수 부분의 일정 정밀도 미만은 너무 작아서 실제로 큰 영향을 끼치지 않는 부분들이 있었다. 따라서 학습 시에 가중치들의 정밀도를 16bit로 바꿔 학습과 연산에 소모되는 자원을 줄이기 위해 창안된 방법론이 바로 Mixed-Precsion Training이다.

왜 ‘mixed’냐면 학습 시에 실제 16bit만을 사용하여 연산을 진행하게 되면, 가중치가 없데이트 될 때, 16bit의 데이터가 표현 가능한 값 미만으로 가중치가 업데이트 되면서 underflow가 나게 되고 -inf, inf, nan의 값등으로 표현되기 때문이다. 따라서, 순전파 시에는 16bit를 사용하고, 가중치를 업데이트할 때는 32bit의 정밀도를 사용하여 가중치를 업데이트하는 16bit/32bit의 ‘섞인’ 정밀도를 사용하기 때문이다.

Mixed Precision Methodolgy

Mixed Precision의 기법은 크게 3가지 단계로 요약 될 수 있다.

Single-Precision(FP32)의 모델의 가중치, activations, gradient 등을 복사하여 보관
(Master Copy of Weights/Gradients)
매우 작은 기울기를 보존하기 위한 loss scaling
메모리에 가중치를 저장하기 이전에 산술 연산시 32bit로 실행하여 누적한 후 16bit로 저장

Master Copy of Weights/Gradients

필수적으로 FP32를 사용해야 하는건 아니지만, 널리 사용되는 데에는 두가지 이유가 있다.

업데이트 되는 가중치가 너무 작아서 16bit의 정밀도로 표현이 불가능한 경우, 가중치의 약 5% 정도가 -24의 지수 스케일을 가지고 있었다. 16bit의 경우 [-14, 15]의 지수만 표현 가능.
현재 가중치에 비해 업데이트 가중치가 너무 작은 경우. 두 값의 비율이 2048배가 넘어가면, FP16의 가수부의 정밀도가 10bit이기 때문에 둘의 합연산시 발생하는 bitshifting으로 인해, 해당 가수부의 표현범위를 벗어나 zero가 되는 경우가 발생하곤 했기 때문이다.

따라서 FP16으로 학습할 때도 발생하는 두 개의 문제 모두 FP32의 정밀도를 가지고 있고 weight업데이트 시에 사용하면 해결되는 문제이다.

Loss Scaling

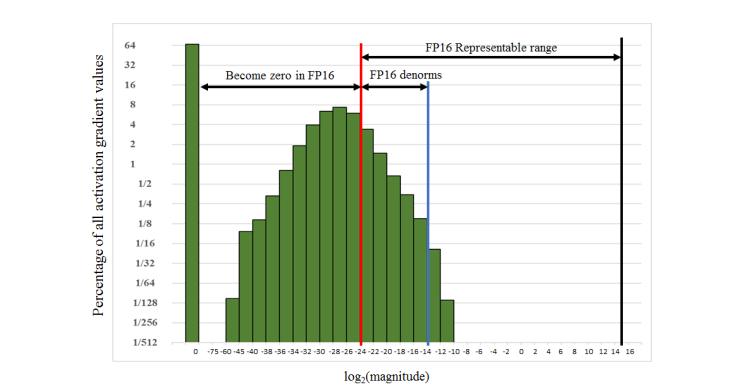
FP16의 지수부로 포현 가능한 범위는 [-14, 15] 이다. 하지만, 실제로는 더 작은 기울기가 더 빈번하게 사용된다. 특히, FP16이 표현가능한 범위의 가중치들은 잘 사용되지 않고 그보다 더 작은 값들이 사용된다. 위의 이미지는 논문에 삽인된 이미지로, 가중치에 대한 히스토그램을 그려놓은 것이다. 지수 값 0을 제외한 36%의 가중치의 히스토그램 분포임을 알 수 있다. 위의 차트에서 보다시피 FP16의 지수부 내에 들어와 있는 가중치의 양은얼마 되지 않음을 알수 있고, denormalized 된 영역까지 합쳐도 상당히 적음을 알 수 있다. 이때, loss를 scaling 하는 것으로 더 작은 값들을 FP16이 표현가능한 범위로 scaling 해줄 수 있다. 8로 loss를 scaling 해주는것으로 FP32로 학습 시켰을 때와 유사한 정확도를 보일 수 있다.

방안은 역전파 전에 순전파가 종료된 시점에서 가중치들을 scaling up해주는 것이다. 어차피 이는 chain rule에 의해 똑같은 양이 각 가중치로 전파되기 때문이다. 이는 다만 가중치에 합산 되기 전에 원래의 ragne로 돌리는 unscaling 작업이 필수적이다. 이는 역전파 직후에 바로, 기울기 관련 계산 전에 discaling해주는 것이 가장 간단하다.

scaling에 필수적인 Scaling Factor를 지정하는 방안은 다음과 같다.

간단하게 상수를 이용해도 됨
상수의 범위가 FP16으로 표현가능한 범위의 값보다 큰 값만 아니면 됨, 상수 값이 그보다 커도 됨
overflow가 날 때는 기울기 업그레이드를 스킵하고 다음 반복으로 넘어가면 됨.

Constant Scaling Factor

가중치의 최대 절대값과 상수의 곱이 65,504(FP16으로 표현가능한 최대값)를 넘지 않도록 고르면 됨.

Dynamic Scaling Factor

상수의 값을 동적으로 정해도 된다. 아래는 동적으로 Scaling Factor S를 구하는 방법이다.
- 임의의 스케일링 팩터 S를 선정한다.
- forwardpass 후의 로스값을 확인.
- 만약 inf나 Nan값이 있다면, backward pass를 진행하지 않고 다음 반복으로 넘어감.
- S의 값을 줄임
- 만약 inf나 Nan값이 없다면 가중치 업데이트를 진행 후 S의 크기를 키움.

대체적으로 실험시에 스케일링 팩터를 키우게 될 수록 정확도가 오르는 경향이 있었다. 이는 어떻게 보면, 당연한게 scaling factor가 커지면 커질수록 fp32이에서 fp16이 표현불가능한 범위의 정밀도를 더 많이 가져올 수 있기 때문이다. 물론 너무 커지면 다시 성능이 줄어들기는 했다.

Arithmetic Precision

신경망 모델에서 실행되는 산술연산은 크게 3가지 범주 안에 들어가게 된다.

벡터의 내적

내적의 누적연산이 들어가는 경우 메모리에 FP16으로 쓰기 전에 FP32로 복원하여 계산한 후 다시 FP16으로 계산해줘야 한다. 이 과정이 존재하지 않는다면, 몇 개의 모델들은 만약 FP32로 누적연산을 수행하지 않는다면, 정확도에서 손해를 보게 된다.

Reduction

reduction은 여러 개의 숫자 정보를 하나로 합치는 것을 뜻한다. 누적합이나, 누적곱, min, max 등을 얘기하며, 신경망에서는 loss나 가중치를 업데이트 하는 경우를 뜻한다.
Large Reduction (batch noramlization, 이나 softmax의 경우)는 FP32로 수행해줘야 정확한 결과가 보장됨을 알 수 있었다. 메모리에는 FP16으로 저장하지만, 연산시에는 FP32로 수행해줘야 한다.

point-wise operations

비선형적인 내적이나, element-wise 행렬 곱 연산의 경우 memory-bandwith가 제한되어 있기 때문에, 산술연산 시의 정밀도는 크게 상관없어서 FP16이나 FP32를 써도 무방하다.

전체 과정 요약

초기값을 32bit의 precision으로 생성
(매반복마다) 16bit의 복사본 값을 생성
forward pass 진행
결과 loss 값에 Scaling Factor S를 곱해줌
backward pass 진행
backward pass의 결과값을 Scaling 을 S로 나눠주면서 해제시킴 (다시 32bit화)
초기값에 unscaling 된 결과값을 더하여 저장함.

코드 구현

넘파이를 활용한 간단한 MLP 모델에서, mixed precision을 구현해 봤다. 논문의 결과처럼 명확하게 정확도가 거의 차이나지 않는 것은 아니다. 이는, 몇가지 과정, 특히 Arithmetic Precision의 과정들을 엄밀하게 지키지 않아서 벌어지는 일일 가능성이 높다고 생각된다. 다만 mixed precision의 과정들을 하나하나 구현하면서 이해하는 것에 중점을 두었다. 비교를 위해서 MixedPrecision이 사용되지 않은 MLP 버전과, MixedPrecision이 사용된 MLP 버전을 같이 삽입하였다.

MLP - numpy

# 해당 코드는 밑바닥부터 딥러닝과 gpt를 통해 생성된 코드입니다.
class MLP:
    def __init__(self, input_size, hidden_sizes, output_size):
        self.input_size = input_size
        self.hidden_sizes = hidden_sizes
        self.output_size = output_size

        # 가중치 초기화
        layer_sizes = [input_size] + hidden_sizes + [output_size]
        self.weights = [np.random.randn(layer_sizes[i], layer_sizes[i+1]) for i in range(len(layer_sizes) - 1)]
        self.biases = [np.random.randn(1, layer_sizes[i+1]) for i in range(len(layer_sizes) - 1)]

    def sigmoid(self, x):
        return 1 / (1 + np.exp(-x))

    def sigmoid_derivative(self, x):
        return x * (1 - x)

    def softmax(self, x):
        exp_values = np.exp(x - np.max(x, axis=-1, keepdims=True))
        return exp_values / np.sum(exp_values, axis=-1, keepdims=True)

    def softmax_derivative(self, x):
        s = x.reshape(-1, 1)
        return np.diagflat(s) - np.dot(s, s.T)

    def forward(self, x):
        # 순전파 계산
        activations = [x] # input x와 계산된 x가 차례대로 들어가게 됨
        weighted_inputs = []

        for i in range(len(self.weights)):
            weighted_input = np.dot(activations[-1], self.weights[i]) + self.biases[i] # matmul + bias
            weighted_inputs.append(weighted_input)
            if i == len(self.weights) - 1: # 마지막 출력층일 경우
                activation = self.softmax(weighted_input)
            else: # 활성화 함수
                activation = self.sigmoid(weighted_input)
            activations.append(activation)

        return activations, weighted_inputs

    def compute_loss(self, y_true, y_pred):
        # 크로스 엔트로피 손실 계산
        return -np.sum(y_true * np.log(y_pred))

    def compute_output_error(self, y_true, y_pred):
        # 출력층 오차 계산
        return y_true - y_pred

    def compute_hidden_error(self, next_layer_error, next_layer_weights, current_layer_output):
        # 은닉층 오차 계산
        return np.dot(next_layer_error, next_layer_weights.T) * self.sigmoid_derivative(current_layer_output)

    def update_weights(self, activations, errors, learning_rate):
        # 가중치 업데이트
        for i in range(len(self.weights)):
            self.weights[i] += learning_rate * activations[i].T.dot(errors[i])
            self.biases[i] += learning_rate * np.sum(errors[i], axis=0)

    def train(self, X, y, epochs, learning_rate):
        for epoch in range(epochs):
            total_loss = 0
            for i in range(len(X)):
                x = X[i:i+1]
                target = y[i:i+1]

                # 순전파
                activations, weighted_inputs = self.forward(x)

                # 오차 계산
                output_error = self.compute_output_error(target, activations[-1])

                # 역전파를 위한 오차들 초기화
                errors = [output_error]

                # 은닉층 오차 계산
                for j in range(len(self.weights) - 1, 0, -1):
                    error = self.compute_hidden_error(errors[-1], self.weights[j], activations[j])
                    errors.append(error)

                errors.reverse()

                # 가중치 업데이트
                self.update_weights(activations, errors, learning_rate)

                # 손실 계산
                loss = self.compute_loss(target, activations[-1])
                total_loss += loss

            if epoch % 100 == 0:
                print(f"Epoch {epoch}, Loss: {total_loss / len(X)}")

    def predict(self, x):
        activations, _ = self.forward(x)
        return activations[-1]

# 데이터 불러오기
df = sns.load_dataset('titanic')

print(df.columns)

# 필요한 특성 선택
selected_features = list(map(lambda x: x.lower(), ['Pclass', 'Age', 'SibSp', 'Parch', 'Fare', 'Sex', 'Embarked', 'Survived']))
df = df[selected_features]

# 결측치 처리
df = df.dropna()

# 범주형 데이터 처리 (One-hot encoding)
df = pd.get_dummies(df, columns=['sex', 'embarked'])

# 입력(X)과 출력(y) 분리
X = df.drop('survived', axis=1).values
y = pd.get_dummies(df['survived']).values  # 생존 여부를 One-hot encoding으로 변환

# 데이터 정규화
scaler = StandardScaler()
X = scaler.fit_transform(X)

# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# MLP 모델 생성
mlp = MLP(input_size=X.shape[1], hidden_sizes=[8], output_size=y.shape[1])  # 출력층 크기는 클래스 개수에 맞게 설정

# 학습
mlp.train(X_train, y_train, epochs=1000, learning_rate=0.1)

# 테스트 데이터에 대한 예측
predictions = mlp.predict(X_test)

# 예측 정확도 계산
accuracy = np.mean(np.argmax(predictions, axis=1) == np.argmax(y_test, axis=1))
print(f"Accuracy on test set: {accuracy * 100:.2f}%")

'''

Accuracy on test set: 76.22%
'''

Mixed Precision - numpy

class MLP:
    def __init__(self, input_size, hidden_sizes, output_size):
        self.input_size = input_size
        self.hidden_sizes = hidden_sizes
        self.output_size = output_size

        # 가중치 초기화 step1
        layer_sizes = [input_size] + hidden_sizes + [output_size]
        self.weights = [np.random.randn(layer_sizes[i], layer_sizes[i+1]) for i in range(len(layer_sizes) - 1)]
        self.biases = [np.random.randn(1, layer_sizes[i+1]) for i in range(len(layer_sizes) - 1)]

        # scaling factor
        self.S = 128

    def copy_weights(self):
      # 가중치 복사 16bit step2
      self.weights_16 = [w.astype(np.float16) for w in self.weights]
      self.biases_16 = [b.astype(np.float16) for b in self.biases]

    def sigmoid(self, x):
        x = x.astype(np.float16)
        return 1 / (1 + np.exp(-x))

    def sigmoid_derivative(self, x):
        x = x.astype(np.float16)
        return x * (1 - x)

    def softmax(self, x):
        x = x.astype(np.float32)
        exp_values = np.exp(x - np.max(x, axis=-1, keepdims=True))
        exp_values /= np.sum(exp_values, axis=-1, keepdims=True)
        exp_values = exp_values.astype(np.float16)
        return exp_values

    def softmax_derivative(self, x):
        x = x.astype(np.float32)
        s = x.reshape(-1, 1)
        ds = np.diagflat(s) - np.dot(s, s.T)
        ds = ds.astype(np.float16)
        return ds

    # step3
    def forward(self, x):
        # 순전파 계산
        activations = [x] # input x와 계산된 x가 차례대로 들어가게 됨
        weighted_inputs = []

        for i in range(len(self.weights_16)):
            weighted_input = np.dot(activations[-1], self.weights_16[i]) + self.biases_16[i] # matmul + bias
            weighted_inputs.append(weighted_input)
            if i == len(self.weights_16) - 1: # 마지막 출력층일 경우
                activation = self.softmax(weighted_input)
            else: # 활성화 함수
                activation = self.sigmoid(weighted_input)
            activations.append(activation)

        return activations, weighted_inputs

    def compute_loss(self, y_true, y_pred):
        # 크로스 엔트로피 손실 계산
        return -np.sum(y_true * np.log(y_pred))

    def compute_output_error(self, y_true, y_pred):
        # 출력층 오차 계산
        return y_true - y_pred

    def compute_hidden_error(self, next_layer_error, next_layer_weights, current_layer_output):
        # 은닉층 오차 계산
        return np.dot(next_layer_error, next_layer_weights.T) * self.sigmoid_derivative(current_layer_output)

    def update_weights(self, activations, errors, learning_rate):
        # 가중치 업데이트
        for i in range(len(self.weights)):
            self.weights[i] += learning_rate * activations[i].T.dot(errors[i])
            self.biases[i] += learning_rate * np.sum(errors[i], axis=0)

    def train(self, X, y, epochs, learning_rate):
        X = X.astype(np.float16)
        y = y.astype(np.float16)

        for epoch in range(epochs):
            #copy weights step2

            total_loss = 0
            for i in range(len(X)):
                x = X[i:i+1]
                target = y[i:i+1]

                # step2 가중치 복사 (16bit)
                self.copy_weights()

                # 순전파
                activations, weighted_inputs = self.forward(x)

                # 오차 계산
                output_error = self.compute_output_error(target, activations[-1])
                # step4 로스에 스케일링팩터 곱하기
                output_error *= self.S

                # 역전파를 위한 오차들 초기화
                errors = [output_error]

                # 은닉층 오차 계산
                for j in range(len(self.weights_16) - 1, 0, -1):
                    error = self.compute_hidden_error(errors[-1], self.weights_16[j], activations[j])
                    errors.append(error)

                errors.reverse()

                # unscaling 과정
                for idx in range(len(errors)):
                    errors[idx] = errors[idx].astype(np.float32)
                    errors[idx] /= self.S

                # 가중치 업데이트

                # activations 32bit
                for i in range(len(activations)):
                    activations[i] = activations[i].astype(np.float32)

                # weighted_inputs 32bit
                for i in range(len(weighted_inputs)):
                    weighted_inputs[i] = weighted_inputs[i].astype(np.float32)

                self.update_weights(activations, errors, learning_rate)

                # 손실 계산
                loss = self.compute_loss(target, activations[-1])
                total_loss += loss

            if epoch % 100 == 0:
                print(f"Epoch {epoch}, Loss: {total_loss / len(X)}")

    def predict(self, x):
        activations, _ = self.forward(x)
        return activations[-1]
        
        
 ...
 
 '''
 Accuracy on test set: 74.13%

 '''

위에서 달라진 부분을 전체 순서에 맞추어 하나씩 보면서 실제로 구현이 어떻게 되어있는지 확인해보자.

1. 가중치 초기화

가중치를 초기화한다. 이는 위의 MLP와 다르지 않다.

2. 가중치를 16bit로 복사

def copy_weights(self):
   # 가중치 복사 16bit step2
   self.weights_16 = [w.astype(np.float16) for w in self.weights]
   self.biases_16 = [b.astype(np.float16) for b in self.biases]

...

def train(self, X, y, epochs, learning_rate):
       X = X.astype(np.float16)
       y = y.astype(np.float16)

       for epoch in range(epochs):
           #copy weights step2

           total_loss = 0
           for i in range(len(X)):
               x = X[i:i+1]
               target = y[i:i+1]

               # step2 가중치 복사 (16bit)
               self.copy_weights()
               
               #순전파
               activations, weighted_inputs = self.forward(x)

...

train 메소드에서 매 에폭시 순전파 연산을 하기 전에 원본의 가중치를 16bit로 복사하여 가져옴을 알 수 있다.

3. forward를 진행


...

def softmax(self, x):
    x = x.astype(np.float32)
    exp_values = np.exp(x - np.max(x, axis=-1, keepdims=True))
    exp_values /= np.sum(exp_values, axis=-1, keepdims=True)
    exp_values = exp_values.astype(np.float16)
    return exp_values

def sigmoid(self, x):
    x = x.astype(np.float16)
    return 1 / (1 + np.exp(-x))

...

def forward(self, x):
     ...

forward 과정 역시 혹시라도 있을 32bit로 자동 타입 캐스팅을 방지하기 위해 활성화 함수와 출력층 함수에서 한 번 더 16bit로 명시적으로 타입을 확정해준다. 이 외에는 MLP의 forward 함수와 같은 방식으로 동작한다.

4. 결과 loss 값에 Scaling Factor S를 곱해줌

def train(self, X, y, epochs, learning_rate):
...
    # step4 로스에 스케일링팩터 곱하기
    output_error *= self.S
...

forward 함수를 통과하고 나온 loss 값에 scaling Factor self.S를 곱해준다.

5. backwardpass 진행

역전파의 과정은 MLP의 과정과 다르지 않다.

6.backward pass의 결과값을 Scaling 을 S로 나눠주면서 해제시킴 (다시 32bit화)

# unscaling 과정
for idx in range(len(errors)):
    errors[idx] = errors[idx].astype(np.float32)
    errors[idx] /= self.S

미리 typecasting을 해주지 않고 self.S로 나눌 경우 언더플로우가 일어나게 되는 경우가 있으므로, 먼저 typecasting을 해줘야 이를 방지할 수 있다.

7. 초기값에 unscaling 된 결과값을 더하여 저장함.

unscaling 결과값을 다시 가중치를 업데이트하는데 사용한다. 이 과정은 MLP의 과정과 다르지 않다.

위의 구현 과정은 실제 pytorch나 허깅페이스에 구현되어 있는 MixedPrecision의 과정과 당연히 100% 동일하지 않다. 다만, 전체 과정을 이해하는 데에는 무리가 없을 것으로 생각된다. 사실 이를 프레임워크에서 사용하는 방식은 함수 몇개를 불러오면 끝이다. 하지만, 시장에서 요구 되는 프레임워크가 지속적으로 바뀌고 있기 때문에 너무 하나의 프레임워크에 의존적이기 보단 이러한 원리를 이해하고 있는 편이 적응과 딥러닝 엔지니어로서의 소양을 함양하는데 더 도움이 되리라 생각한다.

What Every User Should Know About Mixed Precision Training in PyTorch

Mixed Precision Training

Train With Mixed Precision