BufferedWriter/Reader
Codeup1084 문제에서 BufferedWriter를 써야만 통과할 수 있었는데 그 이유는 Scanner로는 출력속도가 느리기 때문이었다.
버퍼를 이용해서 읽고 쓰는 함수인 만큼 입출력의 효율이 비교적 훨씬 좋다.
예를 들면, 벽돌을 나르는데 Scanner는 한 개씩 들고 가는거라면 BufferedReader는 카트에 가득 담아서 한 번에 실어 나르는일과 같다.
-
BufferedReader : 입력 받는다 like
Scanner(System.in) -
BufferedWriter : 출력한다 like
System.out.print()
왜 Buffered를 써야하는지 개념은 잘 이해했다.
아래는 백엔드 위키에서 작성된 정답 코드이다.
public class Codeup1084 {
public static void main(String[] args) throws IOException {
Scanner sc = new Scanner(System.in);
int red = sc.nextInt();
int green = sc.nextInt();
int blue = sc.nextInt();
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int cnt = 0;
for (int i = 0; i < red; i++) {
for (int j = 0; j < green; j++) {
String str = "";
for (int k = 0; k < blue; k++) {
str += i + " " + j + " " + k + "\n";
cnt += 1;
}
bw.write(str);
bw.flush();
}
}
System.out.println(cnt);
}
}이 코드에서 궁금했던건
String str = "";
bw.write(str);
bw.flush();의 위치가 왜 k반복문 밖에 위치해야만 하는지가 궁금했다.
다른 위치에 써놓으면 속도문제로 통과하지 못했기 때문이다.
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.OutputStreamWriter;
import java.util.Scanner;
public class Codeup1084 {
public static void main(String[] args) throws IOException { // Exception 처리
Scanner sc = new Scanner(System.in);
int red = sc.nextInt();
int green = sc.nextInt();
int blue = sc.nextInt();
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int cnt = 0;
for (int i = 0; i < red; i++) {
for (int j = 0; j < green; j++) {
for (int k = 0; k < blue; k++) {
String str = ""; // str이 길어지기 전에 write만 해버리고 str 초기화
str += i + " " + j + " " + k + "\n";
cnt += 1;
bw.write(str);
}
}
}
bw.flush(); // flush 는 마지막에 한 번에 처리하는 코드
System.out.println(cnt);
}
}주말이라 멘토님이 안계셔서 디코로 원기님에게 여쭤보았다.
원기님의 답변으로 바로 위의 코드가 제일 빠르게 속도를 처리한다고 했다.
flush가 마지막에 한 번에 찍어주기 때문에 반복문 안쪽에 있을수록 더 많은 출력을 하는게 이유였다.
BufferedWriter랑 for문 내부 중첩을 주의할 것


주말에도 상세한 답변해주신 원기님께 다시 한번 감사하다.
부동소수점
실수를 표현할 때 소수점의 위치를 고정하지 않는 것을 말한다

10진수
314,600,000 -> 3,146 × 10^5
0.0000451 -> 451 × 10-7
부동소수점 방식
+(부호) 3,146(가수부) E5(지수부)
+(부호) 451(가수부) E-7(지수부)
- float :
32bit의 크기 실수 타입
부호1bit지수8bit가수32bit
대략 7자리의 정밀도를 가짐
→ 1.000000 (%f로 출력했을때 소수점 6자리로 출력)
float f2 = 1.23e10f; = 123억
float fOne = 1.0f;
초기화 값 뒤에 f 를 붙이지않으면 double로 인식
f 를 붙였을 때 6자리를 초과하면 반올림 되어 출력
- double :
64bit의 크기 실수 타입
부호1bit지수11bit가수52bit
대략 15자리의 정밀도를 가짐
→ 1.00000000000000
정밀도가 높지만 메모리 사용량이 더 많음.
그로 인해 애플리케이션의 성능 저하와 문제가 발생할 수 있다.
float의 자릿수가 넘어가면 double로 선언하기
// float 변수 선언 및 초기화, 숫자 뒤에 f를 붙인다.
float f1 = 3.14f;
float f2 = 1.23e10f;
// double 변수 선언 및 초기화
double d1 = 3.141592653589793;
double d2 = 1.23e100;
// 실행결과
f1 = 3.14
f2 = 1.23000003E10
d1 = 3.141592653589793
d2 = 1.23E100
result1 = 6.28 // f1 * 2
result2 = 1.5707963267948966 // d1 / 2BigDecimal: 부동소수점을 정확하게 다룰 수 있는 클래스이며 소수점 아래 자리수를 원하는 만큼 지정이 가능하다.
import java.math.BigDecimal; // BigDecimal import
public class Remind {
public static void main(String[] args) {
// 생성자 + 문자열로 초기화하는 방법
BigDecimal value1 = new BigDecimal("12.23");
// 아래와 같이 사용하면 안 된다.
// 12.230000000000000426325641456060111522674560546875 근사치 오류
BigDecimal dontDoThis = new BigDecimal(12.23);
System.out.println(value1); // 12.23
System.out.println(dontDoThis); //12.2300000000000004263256414560...
}
}특정 자리수에서 반올림 : 소수를 특정 자리수에서 반올림하는 방법을 사용하여 근사치 오류를 줄일 수 있다.
-
Overflow (오버플로우) : 메모리의 표현 범위에서 벗어난 수의 값을 저장하는 경우
-
Underflow (언더플로우) : 메모리가 표현할 수 있는 수보다 적은 수의 값을 저장하는 경우
실수형에서 오버플로우가 발생하는가?
정수형에서는 표현 범위를 넘어가면 오버플로우가 발생하지만 실수형에서는 오버플로우가 발생하면 변수의 값이 무한대가 된다.
또한 정수형에 있는 언더플로우는 실수형에서는 실수형으로 표현할 수 없는 작은값으로 0이 된다.
출처 : 멋사 5기 백엔드 위키 7팀, 13팀
Float의 범위
지수부는 0 ~ 255 에서 언더플로우를 위한 0과 오버플로우를 위한 255를 제외 1 ~ 254까지 표현가능
지수부에 들어가는 값은 음수/양수를 구분하기위해 127을 더한다.
→ 지수부에 127 - 3 = 124
→ 지수부에 127 + 7 = 134
표현 가능한 지수범위 -126 ~ 127
1은 -126
127은 0
254는 127
~ 까지 표현 가능
= 1.17 x = 1.17E-38
= 1.17 x = 1.17E38
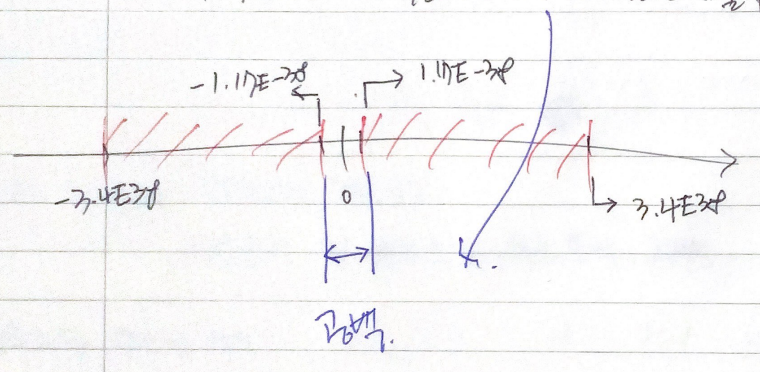
부호가 양수일 때 최소 1.17E-38 ~ 3.4E38 범위까지
부호가 음수일 때 최소 -3.4E38 ~ -1.17E-38 범위까지
최종적으로 -3.4E38 ~ 3.4E38
float 가장 작은 양수 1.17E-38
float 가장 큰 음수 -1.17E-38
양수일 때 1.17E-38 보다 작으면 언더플로우
음수일 때 -1.17E-38보다 크면 오버플로우
-3.4E38 ~ 3.4E38
-1.17E-38 ~ 1.17E-38 까지는 표현이 불가능함
출처 : 백엔드 5기 이희준님
