이 글은 엔지니어 대한민국 님의 영상을 참조하였습니다.

https://www.youtube.com/channel/UCWMAh9cSkEn8v42YRO90BHA/videos

📌 Heap 이란?

최대값이나 최소값을 빠르게 찾아내기 위해 완전 이진트리를 기반으로 한 자료구조

최소힙
최대힙이 존재

최대힙은 최소힙에서 숫자만 반대로 바꾼 형태

📌 동작과정

최소 힙에 노드 삽입

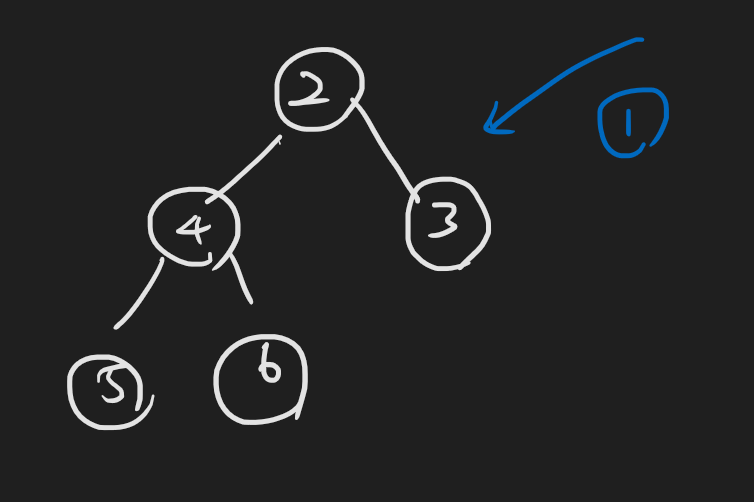
complete binary tree의 구조를 유지하게 마지막의 왼쪽부터 채워나감

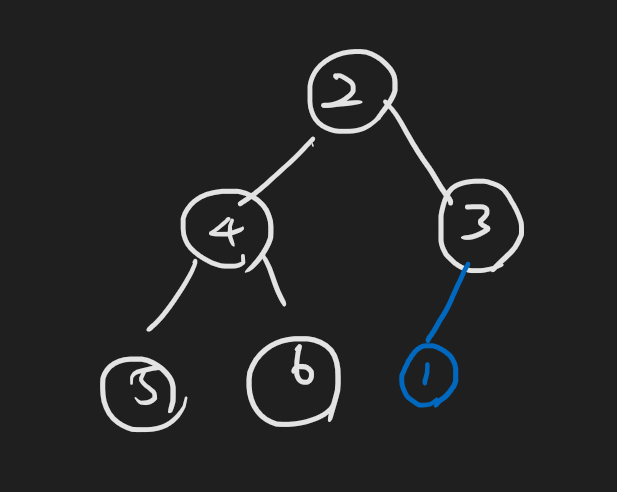
현재는 정렬이 돼있지 않은 상태

부모노드와 비교해서 값이 작으면 자리를 바꿈

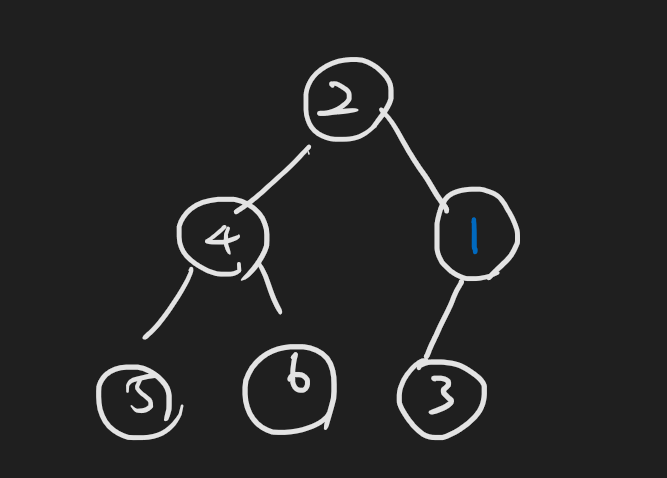
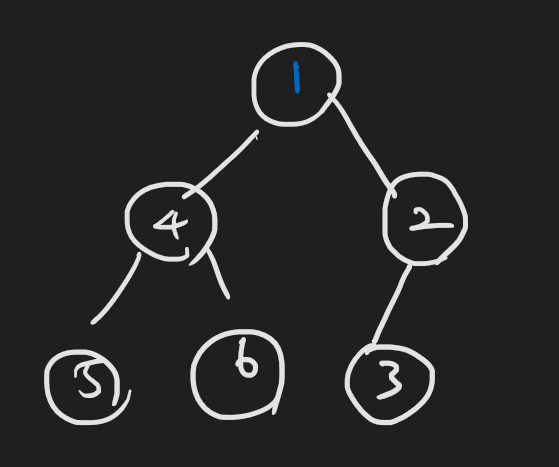
노드가 루트에 도착했거나, 부모노드보다 클때까지 계속 반복한다.

O(logN) 의 시간 복잡도
한번 차수가 떨어질때마다 1/2이 되니까

📌 최소값 구하기

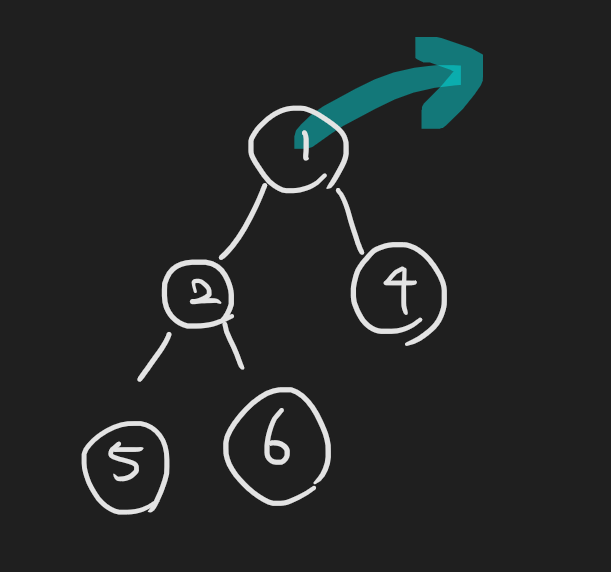
최소값 자체는 루트 노드의 값을 return 하면 되니까 쉬움

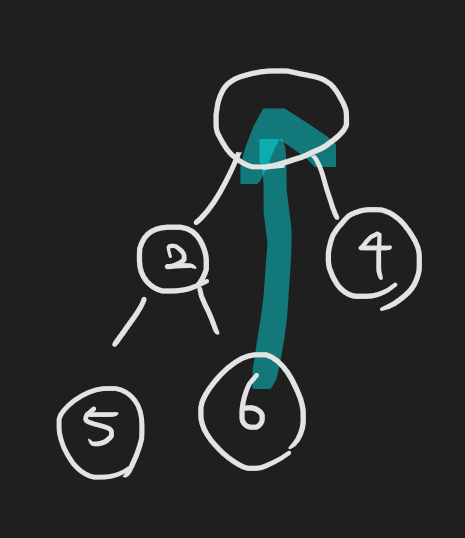
그런데 빈 자리를 채워주어야 함

빈 자리는 말단 노드의 맨 마지막(오른쪽) 값을 가져와서 머리에 채운다.

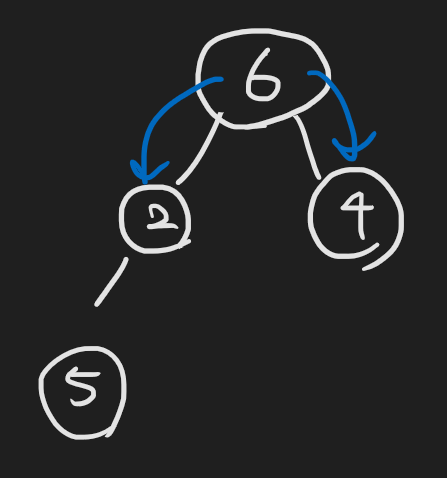
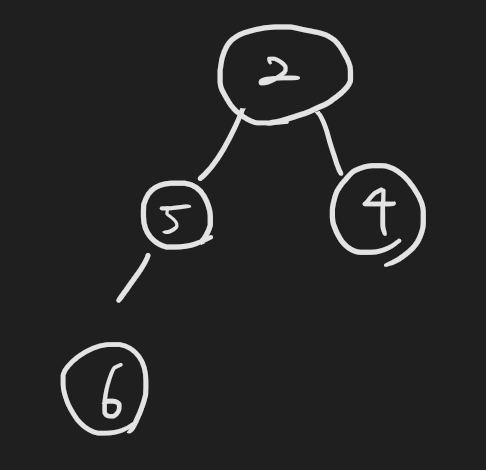
둘 중 더 작은 값과 바꾼다.

자식이 둘다 자기보다 크거나, 해당 노드가 leaf에 도달하면 멈춘다.

📌 Graph 란?

tree는 사실 위에서 아래로만 흐르는 방향 그래프

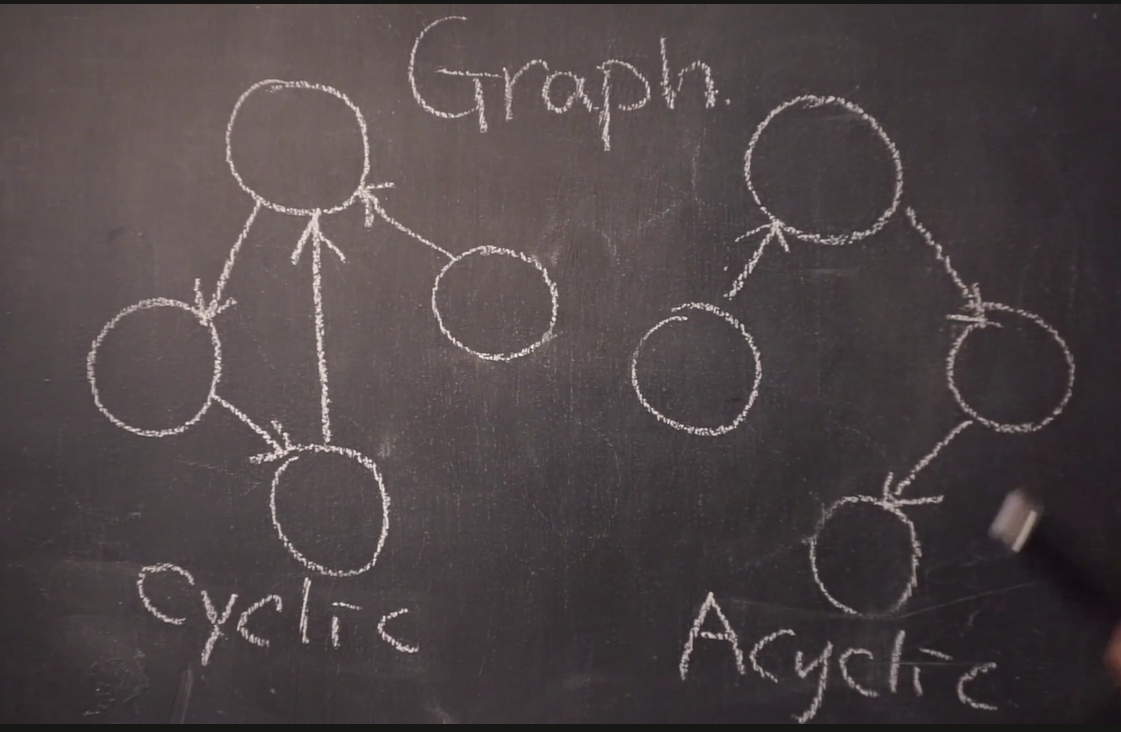
사이클이 있는지 여부로 나눔

🔥 구현방법

graph를 표현하는 방법 2가지

adjacency matrix는 2차원 배열로 표현
adjacency(인접한) list는 linked list로 표현

📌 DFS & BFS

inOrder,preOrder,postOrder는 DFS의 방법

🔥 DFS

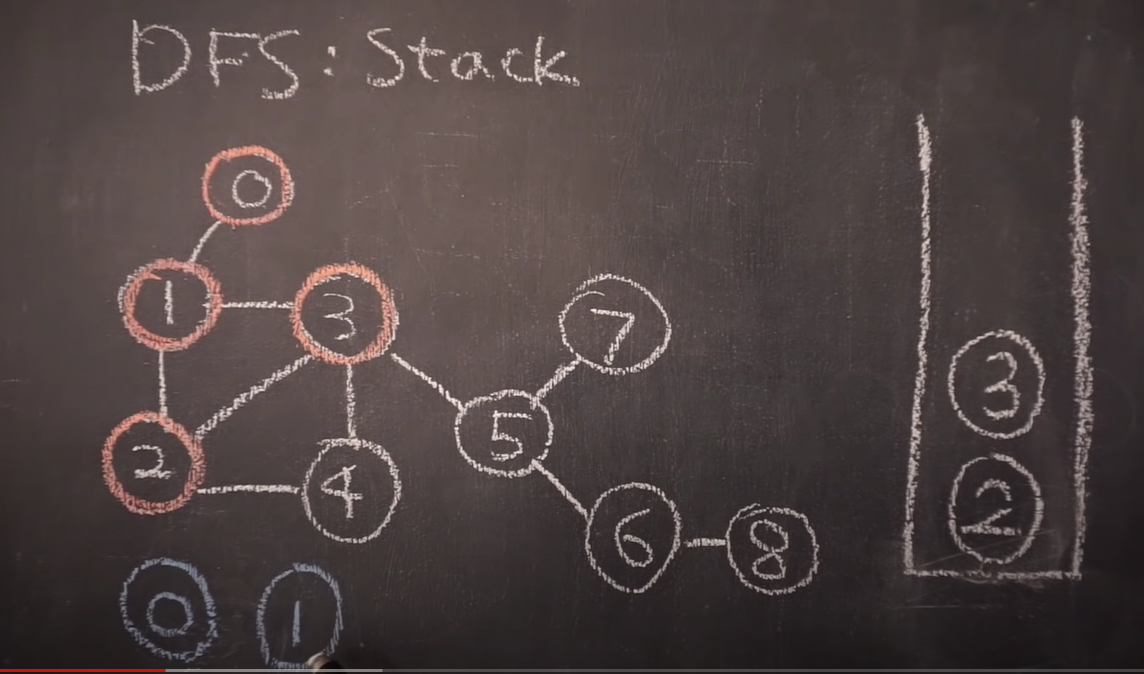
시작노드부터 시작해서 pop() 하면서 인접한 노드들을 넣어준다.

이미 들어갔던 노드들은 다시 넣지 않는다.
이미 들어가있으면 넣지 않는다.
인접한 노드가 없으면 그냥 출력한다.

🔥 BFS

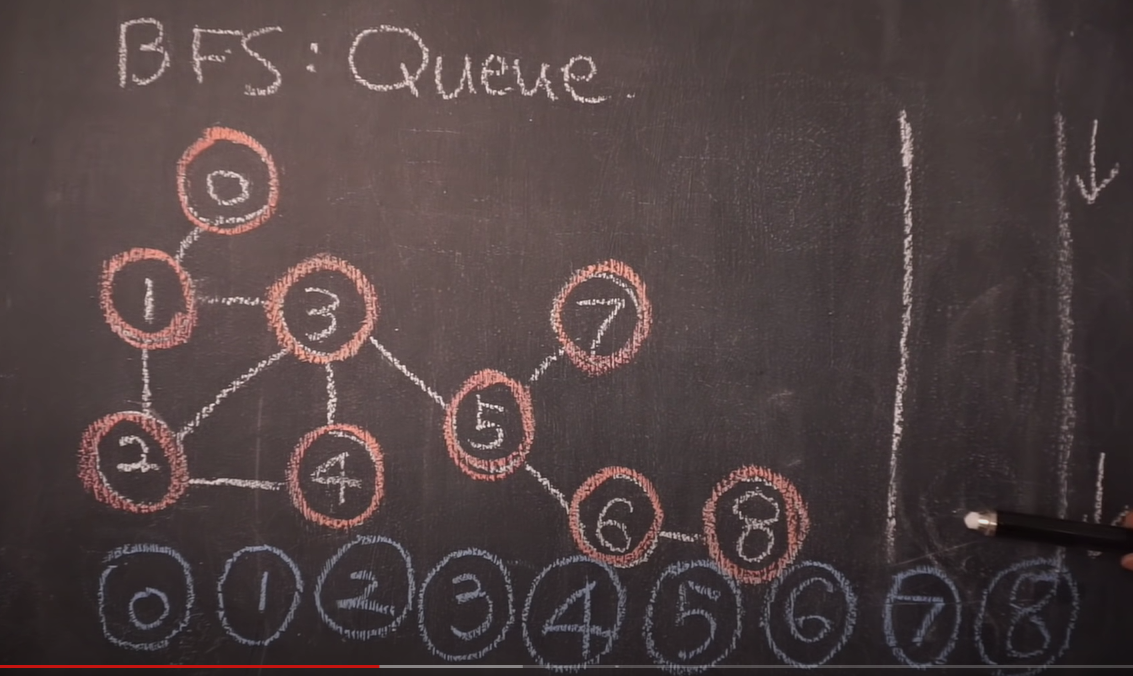
DFS 규칙과 같음

꼭 0부터 시작할 필요는 없다. 어디에서 시작하든지 같은 규칙을 갖고 출력이 된다.

🔥 DFS with Recursion

DFS를 구현할 때 재귀함수를 이용하면 훨씬 간결하고 세련돼진다.

노드에 방문하면 data를 출력하고, 인접한 노드를 순서대로 재귀호출한다.

📌 문제

graph에서 두개의 노드가 서로 찾아갈 수 있는 경로가 있는지 확인하는 함수를 구현하라.

PASS

📌 배열을 이진 검색 트리로

정렬이 돼있고, 고유한 정수로만 이루어진 배열이 있다.
이 배열로 이진 검색 트리를 구현하라.

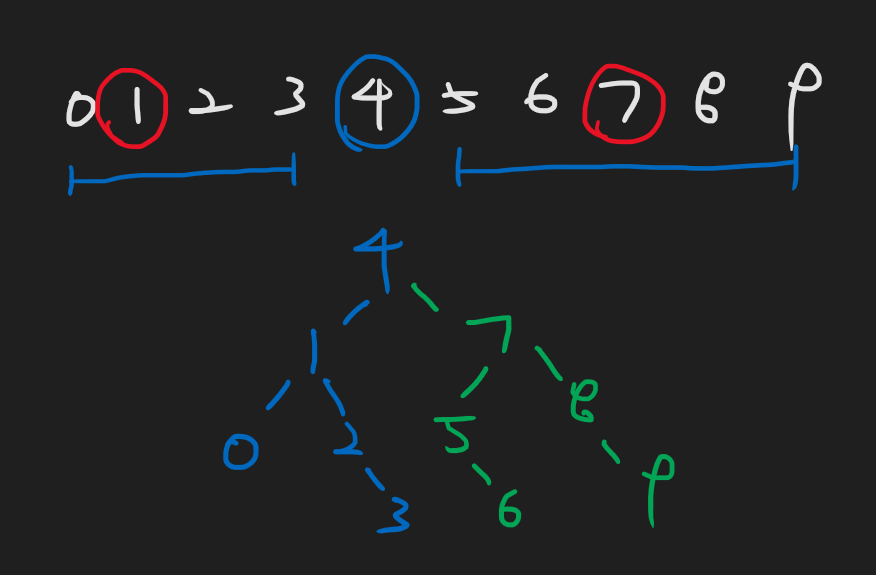
중간점 짝수일 때는 왼쪽꺼 선택

다음 중간점은 전 중간점의 자식노드

🔥 코드

public class ArrayToBinaryTree {
    public static void main(String[] args) {
        int[] a= new int[10];
        for(int i=0;i<10;i++){
            a[i]=i;
        }

        Tree t = new Tree();
        t.makeTree(a);
        t.searchBTree(t.root,2);
    }
    static class Tree{
        class Node{
            int data;
            Node left;
            Node right;

            Node(int data){
                this.data=data;
            }
        }
        Node root;
        void makeTree(int[] a){
            root = makeTreeR(a,0,a.length-1);
        }

        private Node makeTreeR(int[] a, int start, int end) {
            if(start>end) return null;
            int mid = (start+end)/2;
            Node node = new Node(a[mid]);

            // 여기 재귀부분이 핵심
            node.left=makeTreeR(a,start,mid-1);
            node.right=makeTreeR(a,mid+1,end);
            return node;
        }
        void searchBTree(Node n,int find){
            if(find<n.data){
                System.out.println("data is smaller than " + n.data);
                searchBTree(n.left,find);
            }else if(find>n.data){
                System.out.println("data is bigger than " + n.data);
                searchBTree(n.right,find);
            }else{
                System.out.println("data found");
            }
        }
    }
}

recursion에서

private Node makeTreeR(int[] a, int start, int end) {
    if(start>end) return null;
    int mid = (start+end)/2;
    Node node = new Node(a[mid]);

    // 여기 재귀부분이 핵심
    node.left=makeTreeR(a,start,mid-1);
    node.right=makeTreeR(a,mid+1,end);
    return node;
}

• if condition을 넘어가면 2개의 recursion이 돈다. 넘어가지 못하면, recursion을 돌지 못하고 값을 return 한다

라는 것이 포인트