별찍기

현실의 logic이 먼저고, code는 logic에 대응해서 생기는 것.

ex) i= 별에 대응, j= 개행 및 i의 제약조건, k = 공백

귀납과 연역을 적절히 섞어가면서 해야한다. 귀납을 사용하지 않으려는 것은 오만. 아래 별찍기는 모두 귀납법을 기반으로 구현했다. ( 하나 하나 대응시키면서 패턴을 찾았다 )

for문이 진행될 떄마다의 조건을 붙여주어야 한다. ( 다음 조건이 포함돼있어야 함 )

ex) int i=N-2;i>0;i++ (x)
int i=N-2-2*j;i>0;i++ (o)

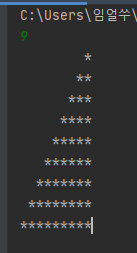
        for(int j=1;j<N+1;j++){
            for(int k=N-j;k>0;k--){
                System.out.print(" ");
            }
            for(int i=0;i<j;i++){
                System.out.print("*");
            }
            System.out.println("");
        }

위와 같이 변수 3개를 사용해서 할 수도 있지만, 2개를 사용하는 방법도 존재

        for(int j=1;j<N+1;j++){
            for(int i=N;i>0;i--){
                if(i>j){
                    System.out.print(" ");
                }else{
                    System.out.print("*");
                }
            }
            System.out.println(" ");
        }

결과는 같다. K를 i와 j의 상관관계를 통해서 제거할 수 있냐 없느냐의 문제.

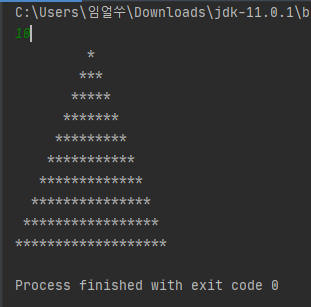
        for(int j=0;j<N;j++){
            for(int k=N-1-j;k>0;k--){
                System.out.print(" ");
            }
            for(int i=0;i<2*j+1;i++){
                System.out.print("*");
            }
            System.out.println("");
        }

K(공백 출력을 위한 변수)를 쓰지 않고 해보려고 했으나 변수가 3개가 필요해 보인다.

        for(int j=0;j<N-2;j++){
            for(int k=N/2-j+N;k>0;k--){
                System.out.print(" ");
            }
            for(int i=0;i<2*j+1;i++){
                System.out.print("*");
            }
            System.out.println("");
        }

        for(int j=0;j<N/2+1;j++){
            for(int k=N/2-j;k>=0;k--){
                System.out.print(" ");
            }
            for(int i=0;i<2*j+1;i++){
                System.out.print("*");
            }
            System.out.println("");
        }

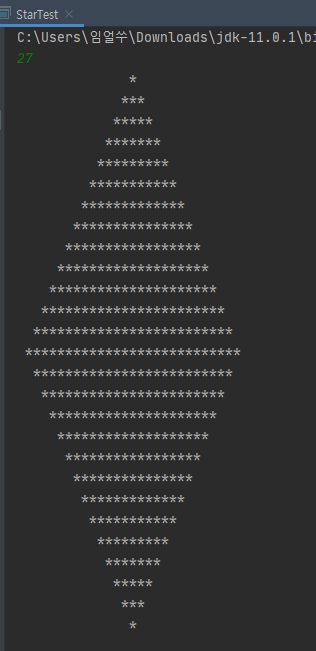
     for(int j=0;j<N/2+1;j++){
            for(int k=N/2-j;k>=0;k--){
                System.out.print(" ");
            }
            for(int i=0;i<2*j+1;i++){
                System.out.print("*");
            }
            System.out.println("");
        }

        for(int j=0;j<N/2;j++){
            for(int k=0;k<j+2;k++){
                System.out.print(" ");
            }
            for(int i=N-2-2*j;i>0;i--){
                System.out.print("*");
            }
            System.out.println("");
        }

위의 구역과 아래의 구역을 붙이는 식으로 구현했다.

아래 구역에서 별의 갯수를 i=2j+1 로 시작하는 걸로 착각해서 뭔가 헷갈렸다.

For loop = 반복되는 갯수만큼 출력