퍼셉트론

머신러닝 공부 - 머신러닝 교과서 with 파이썬, 사이킷런, 텐서플로

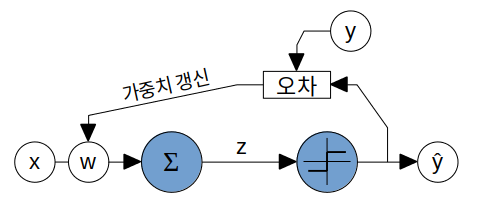
퍼셉트론 perceptron, 인공 뉴런 artificial neuron

• 이진 분류기: +1과 -1 분류
• 입력 $\boldsymbol{x}$와 가중치 $\boldsymbol{w}$의 내적값에 절편 $\boldsymbol{w}_0$를 더한 값이 0보다 크거나 같으면 +1, 작으면 -1 출력
  $\boldsymbol{x}=\begin{bmatrix}x_{1}\\\vdots\\x_{m}\end{bmatrix},\quad \boldsymbol{w}=\begin{bmatrix}w_{1}\\\vdots\\w_{m}\end{bmatrix}$
  $z=\boldsymbol{w}^\top\boldsymbol{x}$
  $\Phi(z) = \begin{cases}+1,\quad z\ge\theta \\ -1,\quad otherwise\end{cases}$
  여기서 임계값 $\theta$를 좌항으로 넘겨 $w_{0} = -\theta$ 절편 정의
  $x_{0}=1$과 $w_{0}$를 각각 $\boldsymbol{x}$와 $\boldsymbol{w}$에 추가하여 표기 간략화
  $z=\boldsymbol{w}^\top\boldsymbol{x}=w_{0}+w_1x_1+\cdots+w_mx_m$
  $\Phi(z) = \begin{cases}+1,\quad z\ge0 \\ -1,\quad otherwise\end{cases}$
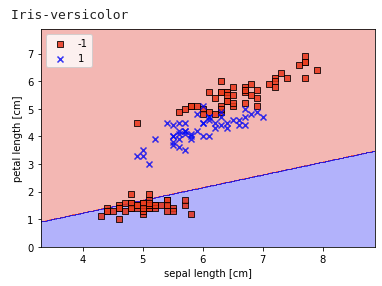
• 데이터가 선형 분리 가능해야 잘 작동한다.

퍼셉트론의 학습

1. 가중치 초기화
2. 훈련 샘플 $\boldsymbol{x}^{(i)}$마다 출력 $\hat{y}$ 계산, 가중치 $\boldsymbol{w}$ 업데이트

• 가중치 업데이트
  $\boldsymbol{w} = \boldsymbol{w} + \Delta\boldsymbol{w}$
  $\Delta\boldsymbol{w}=\eta(y^{(i)}-\hat{y}^{(i)})\boldsymbol{x}^{(i)}$

• $\Delta\boldsymbol{w}$: 현재 가중치 $\boldsymbol{w}$를 변화시킬 방향과 크기
  • $\eta$ 학습률: 가중치 변화의 크기를 조절하는 하이퍼파라미터
  • $(y-\hat{y})\boldsymbol{x}$:
    • 괄호 안의 경우 이진 분류결과가 맞다면 0, 틀리다면 레이블에 따라서 +2, -2 값이 된다.
    • 예를 들어 -1이 target값인데 퍼셉트론이 +1로 예측한 경우, $\boldsymbol{w, x}$의 $w_{j}, x_{j}$에 대해서
      1. $z$의 값을 감소시켜야하므로 $w_{j}x_{j}$의 값을 작게 만들어야한다.
      2. $(y-\hat{y})x_{j}=-2x_{j}$
      3. ${x}_{j}$가 음수인 경우 $\Delta w_{j} >0$이므로 $w_{j}$는 증가하게되고 그 결과 $w_{j}x_{j}$는 작아지게된다.
         ${x}_{j}$가 양수인 경우 $\Delta w_{j} <0$이므로 $w_{j}$는 감소하게되고 $w_{j}x_{j}$는 마찬가지로 작아지게된다.
    • $\boldsymbol{x}$: 가중치의 변화 방향과 크기에 관여. (퍼셉트론의 예측이 틀린 경우 큰 입력값이 $z$값에 크게 영향을 주기때문에 가중치도 입력값의 크기에 맞춰 조절하기위해 단순히 부호를 사용하지 않고 $\boldsymbol{x}$를 쓴건가?)

• $\boldsymbol{w}$를 0으로 초기화하는 경우?
  • $\boldsymbol{w} = \boldsymbol{w} + \Delta\boldsymbol{w} =\Delta\boldsymbol{w} = \eta(y^{(i)}-\hat{y}^{(i)})\boldsymbol{x}^{(i)} = \eta(y^{(i)}-\Phi(z))\boldsymbol{x}^{(i)}= \eta(y^{(i)}-\Phi(0))\boldsymbol{x}^{(i)}= \eta(y^{(i)}-1)\boldsymbol{x}^{(i)}$
  • 가중치 업데이트 후 $\boldsymbol{w}$는 0 또는 $-2\eta\boldsymbol{x}^{(i)}$가 되며 $\boldsymbol{x}^{(i)}$에 의해서 크기, 방향이 결정되고 학습률$\eta$는 오직 크기에만 영향을 주게된다.
  • ❓: $y=-1$인 샘플을 통해서 가중치가 업데이트되면 $\boldsymbol{w} = -2\eta\boldsymbol{x}$ 가 되니 그 다음 스텝부터는 상관없지 않나? 일단 붓꽃 데이터에 대해서는 잘 작동한다.

다중클래스 분류

• 일대다 one-versus-all: 클래스가 여러개인 경우 하나의 클래스를 +1, 나머지를 -1로 취급하여 각 클래스마다 하나의 퍼셉트론을 학습시킨다. 새로운 샘플 예측시에는 전체 퍼셉트론을 사용하여 $z$값이 가장 큰 분류기의 결과를 선택한다.
• 붓꽃 데이터는 선형 분리가 불가능해 다중 클래스 분류가 어렵다.

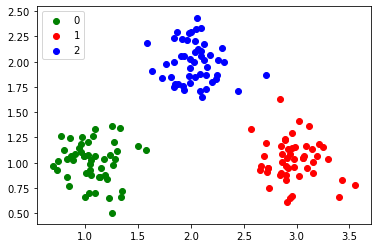
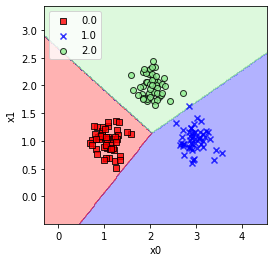
• 임의로 생성한 데이터
  
• 클래스별로 퍼셉트론 학습
  
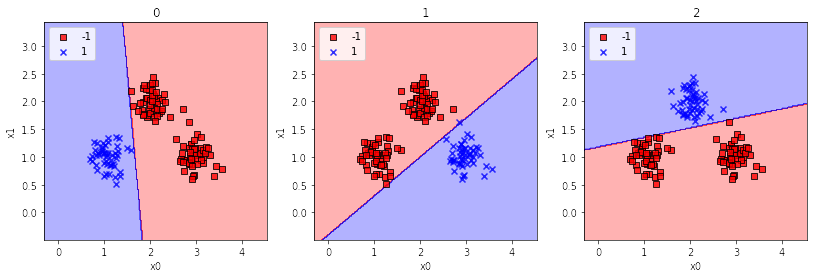
• 각 샘플마다 모든 퍼셉트론 중 가장 큰 z값을 내놓는 클래스를 선택한다.
  

연습: https://github.com/canlion/ml_study - perceptron