알고리즘 복잡도

코드반복문이 시간 복잡도(수행시간)를 좌우함
빅오표기법: 알고리즘 최악의 실행 시간 표기
오메가 표기법: 최상의 실행시간 표기
세타 표기법: 평균실행시간 표기

n : 무한대의 입력의미한다

O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(2^n) < O(n!)
빅오표기법 걸리는 시간 순서는 로그의 값을 구하는 방법만 알면 헷갈리지 않는다.

로그의 밑이 생략된경우 2라는 사실!!

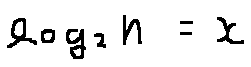
n을 2로 나눈 횟수를 구하면 x 를 구할 수 있다는 사실을 잊지말자!

만약 n이 8이라고 가정한다면 순서를 명확하게 알 수 있다
O(1) < O(3) < O(8) < O(3*8) < O(8^2) < O(2^8) < O(8!)

8! 은 팩토리얼로서 1부터~8까지 숫자들을 곱하는것이다.

O(1) : 무조건 상수회 실행한다 n이 어떤값이든
if(n>10)
{ System.out.println(n); }

O(logn) : 로그의 밑은 생략된경우 2이다. 만약 log8 이라면 3이다

O(n) : 아래 코드에서 수행횟수는 10n 이다 n이 무한대로 가면 10n 이나 n 이나 차이가 없다고 보고 O(n) 으로 표기한다

for(int i = 0; i < 10; ++i)
	for(int j = 0; j < n; ++j)

O(nlogn) :

O(n^2) : 아래 코드에서 수행횟수는 10n^2 이다 n이 무한대로 가면 10n^2 이나 n^2 이나 차이가 없다고 보고 O(n^2) 으로 표기한다

for(int i = 0; i < 10; ++i)
	for(int j = 0; j < n; ++j)
		for(int k = 0; k < n; ++k)

시간 복잡도가 2n^2 + 3n 이라면 가장큰 차수인 2n^2 에서 상수 2를 뺀 n^2 만 표기한다 O(n^2)