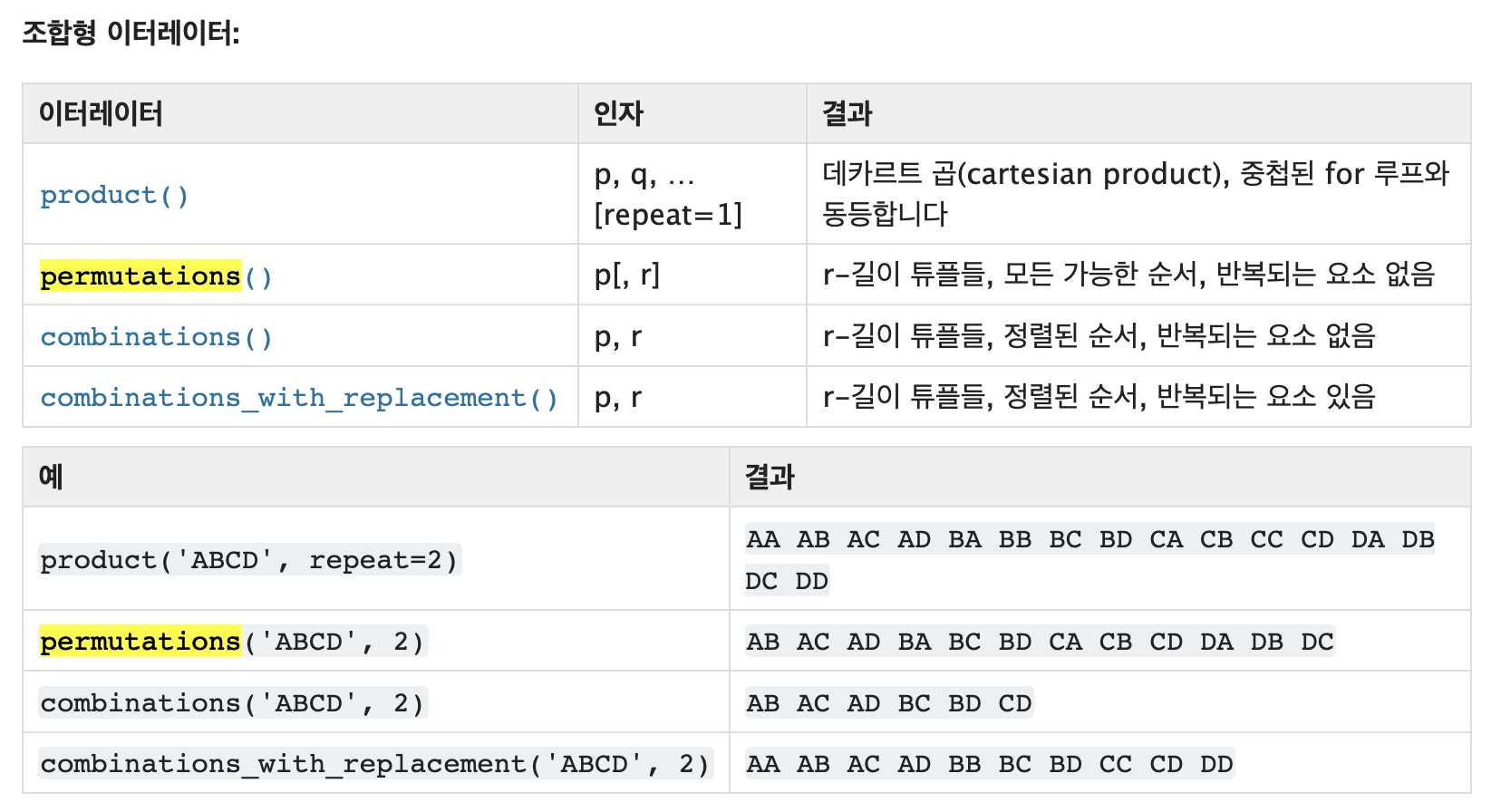
Permutation이란

Permutation은 우리말로 순열이라는 뜻으로 순서가 부여된 임의의 집합을 다른 순서로 뒤섞는 연산이다.

즉 집합의 원소로 만들 수 있는 모든 순서의 조합이라고 할 수 있다.

예를 들면 아래와 같다.

[a,b,c]의 순열 => [a,b,c] , [a,c,b], [b,a,c], [b,c,a], [c,a,b], [c,b,a] => 총 6개가 나온다.

구현 방법

1. dfs를 활용한 방법

import copy

def permutation_1(depth: int, target: str):

    if len(target) == depth:
        return [target]
    
    tmp = copy.deepcopy(target)

    result = []
    for i in range(depth, len(target)):
        tmp[i], tmp[depth] = tmp[depth], tmp[i]
        result.extend(permutation_1(depth+1, tmp))
        tmp[i], tmp[depth] = tmp[depth], tmp[i]
    
    return result

위 방식은 들어온 리스트의 순서를 바꾸면서 순열을 만드는 코드 이다.

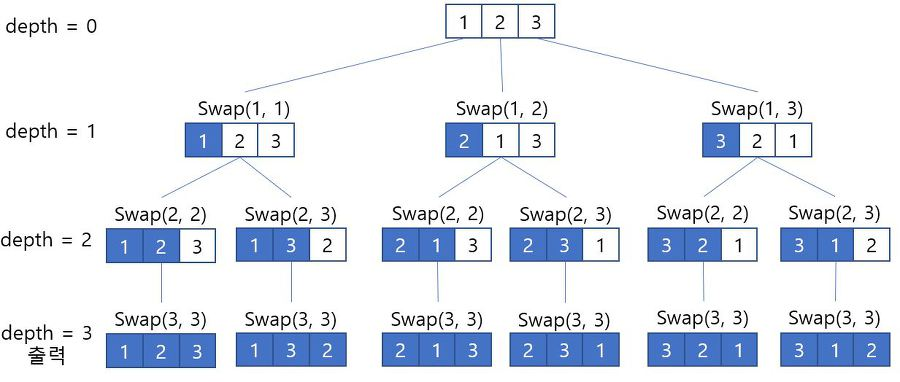
위 그림을 보면 더 쉽게 이해되는데, 깊이가 깊어질수록 자기보다 큰 수를 바꿔가면서 경우의 수를 늘려나간다.

다만 이 코드의 문제는 순열의 순서가 보장되지 않는다. 따라서 순수하게 순열을 찾을 경우, 문제가 없지만 순열 순서가 중요할 경우에는 맞지 않다.

2. dfs 개선 방식

def permutation_2(depth: int, target: list, visited: list, answer: list):

    if len(target) == depth:
        return [answer]

    result = []
    tmp_answer = copy.deepcopy(answer)

    for i in range(len(target)):
        if not visited[i]:
            visited[i] = True
            tmp_answer[depth] = target[i]
            result.extend(permutation_2(depth+1, target, visited, tmp_answer))
            visited[i] = False
    
    return result

print(permutation_2(0, [1,2,3], [False, False, False], [0, 0, 0]))

1번 방식의 문제는 바로 자기 자신을 swap할 때, 순서가 바뀐다는 문제다. 따라서 자기 자신이 사용됐다,(visited)를 체크하여 사용되지 않은 경우에만 스왑을 할 수 있도록 한다.

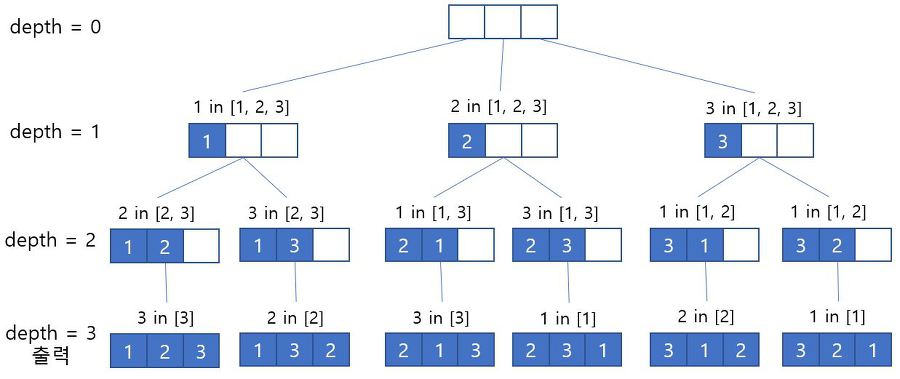
3. itertools 사용

result = list(itertools.permutations([1,2,3], 3))

print(result)

python에서는 itertools라는 이름의 라이브러리를 제공한다. 해당 라이브러리는 itertator, 즉 탐색 관련된 모든 기능을 제공한다.

거기서 permutations이라는 메소드가 있으며 이를 사용하면 쉽게 순열을 구할 수 있다.