two pointer 테크닉이란,
다수의 값들 중 특별한 기준을 맞춘 두 개의 지점 혹은 값을 찾을 때 2개의 지점을 이용하는 것을 말한다.
예를들어, 아래와 같은 문제가 있다고 하자.
- [4, 1, 9, 7, 5, 3, 16] 의 숫자가 있을 때 그 합이 13이 되는 2개의 숫자가 있는지 없는지 구별하시오. 단, 두 개의 동일한 숫자를 사용할 수 없다.
이 때, two pointer 테크닉을 이용하자면 다음과 같이 풀 수 있다.
- 먼저 리스트를 오름차순으로 정렬한다.
- 맨 왼쪽 숫자를 가리키는 Left pointer를 생각하자.
- 맨 오른쪽 숫자를 가리키는 Right pointer를 생각하자.
- L, R pointer가 가리키는 숫자의 합을 생각하자.
- 만약 합이 목표로 하는 값과 같다면, 그러한 숫자가 있다는 결론 [끝]
- 만약 합이 목표로 하는 값보다 작다면, Left pointer를 오른쪽으로 한 칸 옮긴다.
- 만약 함이 목표로 하는 값보다 크다면, Right pointer를 왼쪽으로 한 칸 옮긴다.
- 새로운 L, R Pointer 를 대상으로 위의 과정을 반복
- 만약 두 포인터가 같은 곳을 가리키게 된다면, 그러한 숫자가 없다는 결론 [끝]
그럼 two pointer 테크닉을 적용하면 다음과 같이 풀 수 있다.
-
정렬
- [1, 3, 4, 5, 7, 9, 16]
-
Left pointer → 1, Right pointer → 16, 합이 17
-
17은 13보다 크므로, Right pointer를 왼쪽으로 옮긴다.
-
Left pointer → 1, Right pointer → 9, 합이 10
-
10은 13보다 작으므로, Left pointer를 오른쪽으로 옮긴다.
-
Left pointer → 3, Right pointer → 9, 합이 12
-
12는 13보다 작으므로, Left pointer를 오른쪽으로 옮긴다.
-
Left pointer → 4, Right pointer → 9, 합이 13
-
목표로 하는 값이 나왔으므로, 그 합이 13이 되는 2개의 숫자가 존재한다.
나는 여기서 의문을 가지지 않을 수 없었다.
지금이야 그 2개의 값이 나왔으니 다행이지만, 나오지 않은 경우는 어찌할 것인가?
two pointer는 모든 조합을 조사하지는 않는 것 같은데, 그럼에도 불구하고 2개의 값이 나오지 않은 경우를 신뢰할 수 있는가? 다른 말로, two pointer 테크닉을 증명할 수 있나?
이 부분이 내가 정말 고민하던 부분이었다. 반례를 구하려고도 했었다.(two pointer 테크닉이 2개의 숫자를 찾을 수 없다고 말하지만, 실제로는 그런 조합이 존재하는 경우)
하지만 처참히 실패했다.
다행하게도, 다음 글을 통해 그 힌트를 발견할 수 있었다.
여기서 사용된 방법은 해당 테크닉이 해가 있음에도 없다고 말하는 경우가 없다는 것을 증명한 것이다.
동일한 방법으로 위의 two pointer 테크닉을 다음의 2가지로 증명할 수 있다.
-
Left가 Left 답에 도착하기 전에 Right가 Right 답 왼쪽으로 이동하는 경우가 없다는 것을 증명하면 된다.
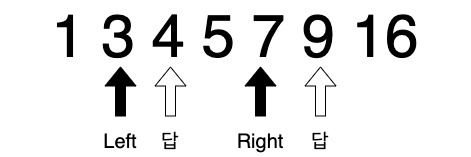
-
Right가 Right 답에 도착하기 전에 Left가 Left 답 오른쪽으로 이동하는 경우가 없다는 것을 증명하면 된다.
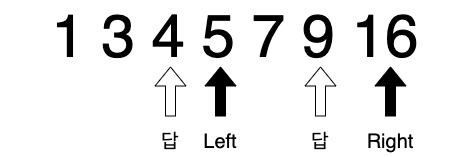
-
첫번째 경우 증명
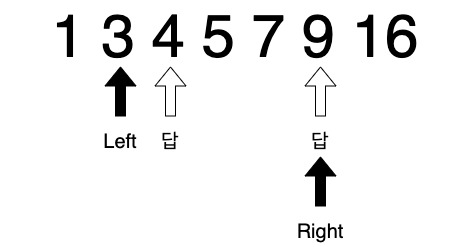
- Right pointer가 답을 지나려면 답 위치에 와야만 한다.
- 이 때, Left pointer와 Right pointer가 가리키는 숫자의 합은 답 pointer가 가리키는 숫자의 합보다 언제나 작다. 왜냐하면 Left pointer가 답의 왼쪽에 있기 때문이다.
- 그렇다면, Right가 아닌 Left pointer가 움직여야 한다. 여기서 Right pointer가 움직일 수 없다.
- 다른말로 하자면, Right pointer가 답 위치에 있다면 움직일 수 있는 것은 Left pointer일 뿐이므로 첫번째 경우와 같은 일이 일어날 수 없다.
-
두번째 경우 증명
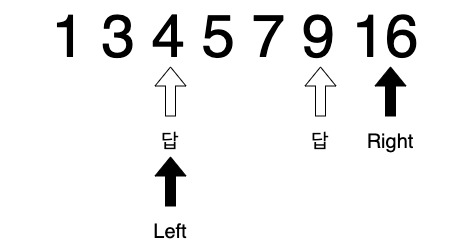
- 이것도 마찬가지이다.
- Left pointer가 답 위치에 있는 경우라면 Right pointer 밖에 움직일 수 없다.
- 왜냐하면 두 포인터가 가리키는 숫자의 합이 답 포인터가 가리키는 숫자의 합보다 무조건 크기 때문이다.
