Algorithm

오백만년만에 알고리즘 문제를 풀었다. 원래 leetcode를 이용할 계획이었지만, 랜덤으로 문제를 뽑았을 때 자꾸 medium 단계가 나와서 프로그래머스 간단한 문제로 방향을 바꿨다. 이 쉬운 2단계 문제를 푸는데도 한참 걸렸다. 열심히공부해야지ㅠㅠㅠㅠㅠㅠ첫번째 문제

작심2일 오늘도 알고리즘 문제를 풀었다~ 여러 타입의 알고리즘 문제를 풀고 좀 익숙해진 다음에 릿코드에서 랜덤으로 문제를 뽑아보기로했당. 오늘의 알고리즘은 분할정복(divide & conquer) 문제링크 백준 #2447. 별찍기 10 풀이방법 큰~ 문제를 작은

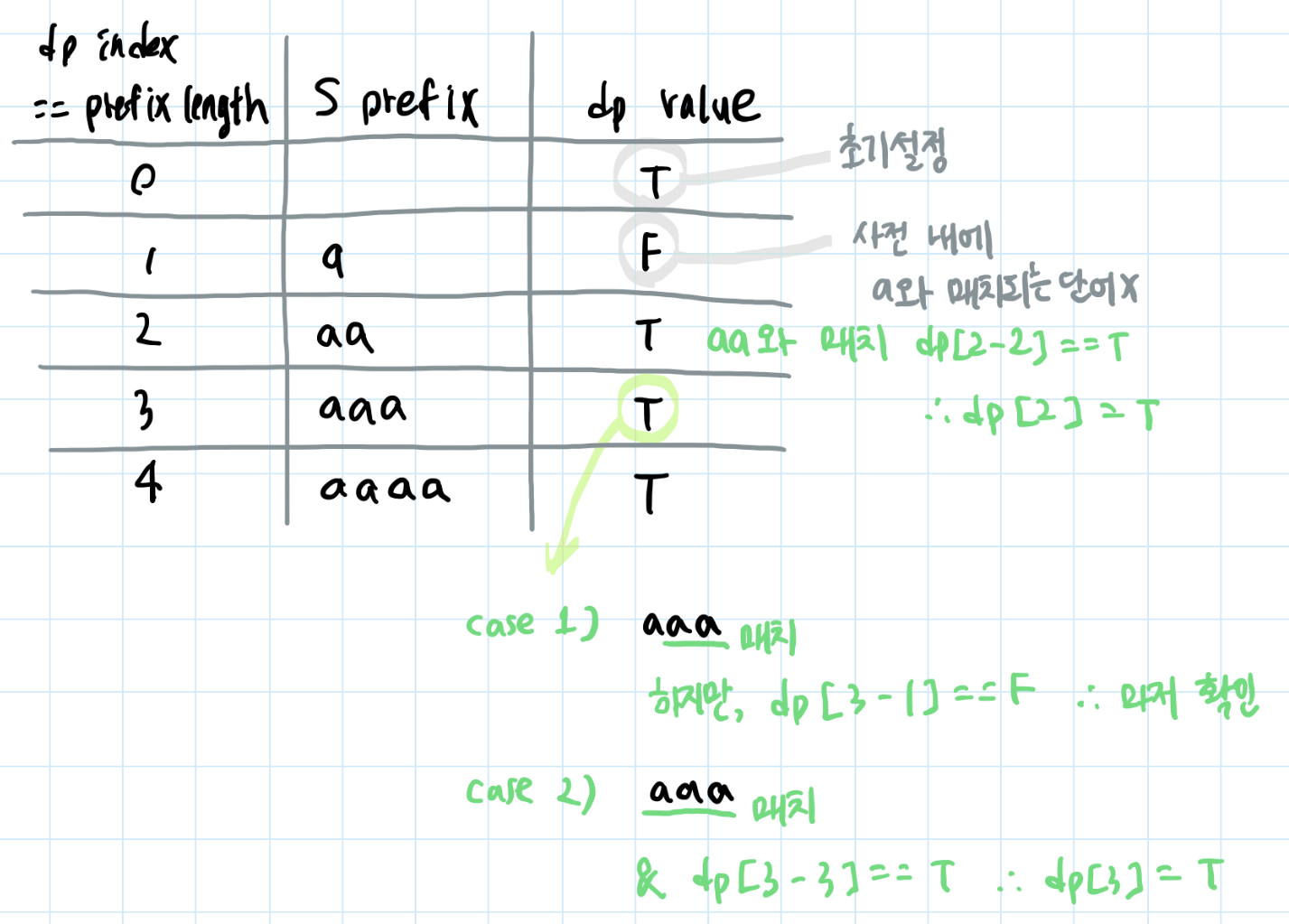
피곤해죽을거같지만 문제를 풀었다 ㅠ\[백준 테스트케이스가 딱 하나다. 그리고 그 테스트케이스는 너무 불친절해서 문제를 똑바로 이해하지 못하기 딱 좋다. 처음에 주어진 테스트케이스를 봤을때 그냥 사전 단어들을 시작 알파벳으로 정리하고 S 내에 매치되는거 확인하면되는거아냐

재밌다 재밌다.........\[백준 "인접한 두 공유기 사이의 거리"를 편의상 D라고 할게용D는 유일한 값을 갖지 않는 값이에요. 범위를 갖고있죠! 그래서 문제에서도 D의 최대값을 물어보고 있죠?? 그래서 그 범위를 점점 좁혀서 구하기로 했습니다.범위를 좁히기 위해

주말 끝 ㅜ,ㅜ\[백준 쉬운 문제였다. 보면 바로 dfs나 bfs로 풀 수 있는 문제인걸 알 수 있다. dfs를 이용해 구역을 탐색했다. 적록색약이 아닌 사람 / 적록색약인 사람 각각 비교를 다르게 해 문제를 해결했다.

백트래킹 유형의 문제~\_~\[백준 3 ≤ L ≤ C ≤ 15 조건 때문에 완전탐색으로 해결 할 수 있는 문제라고 판단했다. 이전의 문제들과 달리 백트래킹을 사용했다. 백트래킹은 완전탐색 알고리즘 중 DFS를 사용하면서 가지치기를 통해 비효율적인 경로를 차단하는 알고리

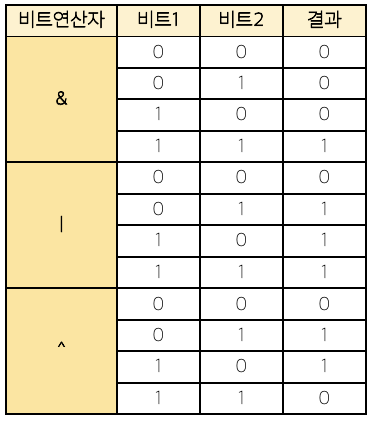
\[백준 데이터들은 0과 1의 집합이라고 하죠. 비트는 네트워크 외에도 운영체제 등에서 자주 접할 수 있습니다. 최적의 성능을 위해 여러 곳에서 쓰이고 있는게 비트인데요, 이 비트를 알고리즘 문제 풀이 내 여러 개의 상태를 표시할 때도 유용하게 쓸 수 있습니다!위에서

의욕이 넘치는 날!!🔥\[백준 메모리가 4mb다 ㅋㅋ... 모.. array나 linkedList로는 해결할 수 없는 문제인걸 알 수 있죠?? 그래서 비트마스킹을 사용했습니다! 비트마스킹은 비트단위로 값을 보존하고, 그걸 이용하는 거죠~ 1 ~ 20 사이의 수만 사용

오랜만에 낮에 하는 코딩😀\[백준 보통 구간 합을 구할때 반복문을 이용해 O(n)의 시간복잡도를 갖는다. 이 문제에서는 전처리를 진행해 O(1)에 구간 합을 구할 수 있도록 했다. (물론, 전처리 과정은 O(n)입니다)pSum이라는 배열에 처음부터 x개 원소의 합을

\[백준 1. PrefixSum을 구하고 각각에 모듈러 연산2\. 같은 모듈러 연산 결과들을 count"부분 합이 M으로 나누어 떨어지는 (i, j)쌍의 개수"\-> (pSumj + 1 - pSumi) % M = 0\-> pSumj + 1 % M = pSumi % M따

워료일.....😇\[백준 정점과 간선 정보가 주어지면 몇개의 트리를 가지고 있는지 판단하는 문제이다.트리의 조건은 다음과 같다.정점이 n개 일때, 간선은 n - 1개 이다사이클이 없다두 정점 사이에 유일한 경로를 갖는다여기서 2, 3번째는 같은 의미를 내포하고 있다고

자료구조를 써보자!\[백준 간단한 문제이다. 값이 이미 존재하는 값인지 확인하고, 그렇다면 해당 값을 지우면 된다. 근데 여기서 사용하는 자료구조가 중요하다. 문제를 파악하면 다음과 같다.배열 A, B 크기의 합을 n이라 하자.search: n번삽입/삭제: n번삽입/삭

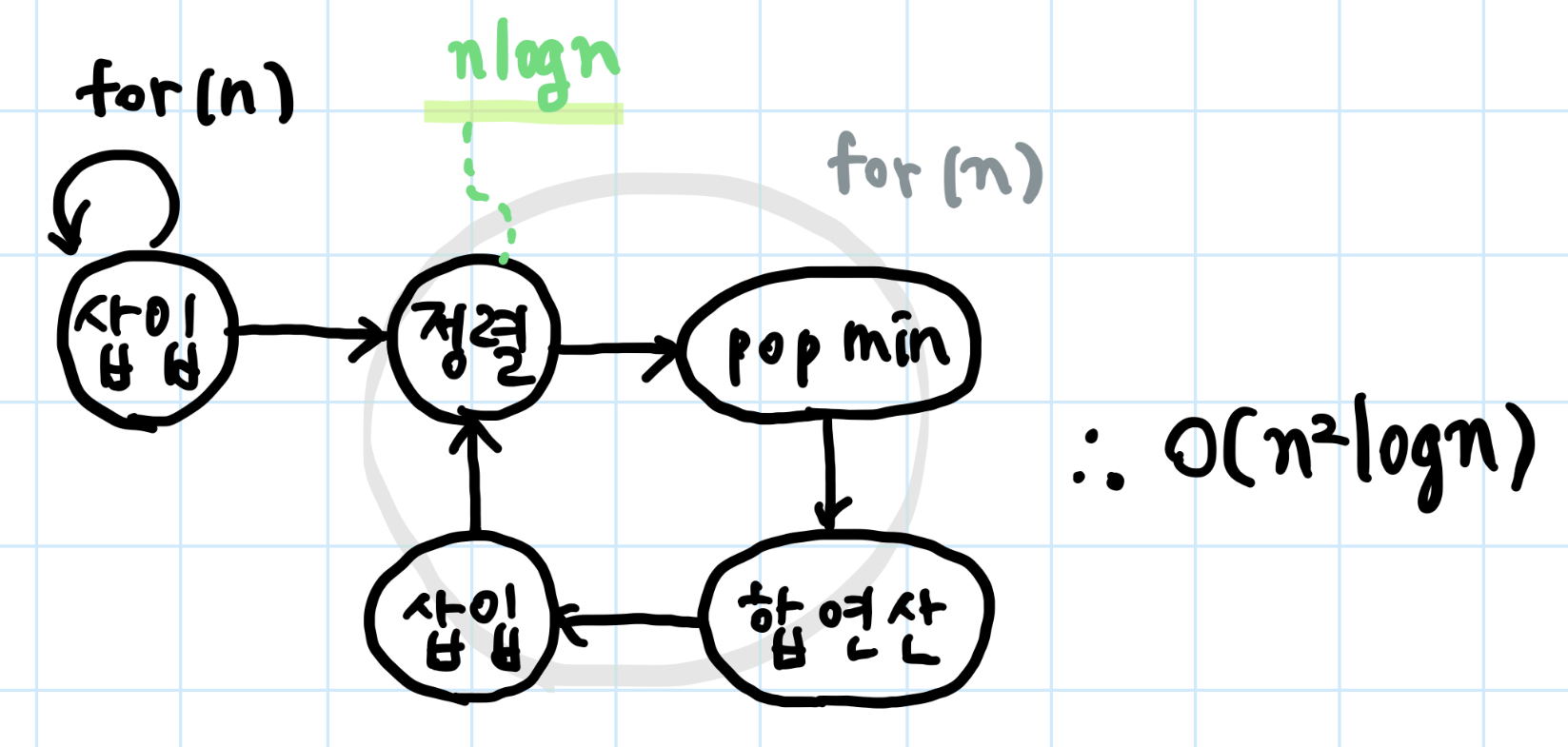
🤒🤒너모추워\[백준 문제를 보면 대애충 (값 삽입) -> {(정렬) -> (합치기) -> (합 결과 삽입)} \* n 이런 흐름으로 문제를 해결한다는 걸 알 수 있죠. 정렬이 자주 일어나고, 정렬의 결과에서 가장 작은 값 두개를 계속 꺼낸다는 풀이 특징을 고려해 문

잼있다 하하 문제링크 백준 #1717. 집합의 표현 풀이방법 유니온파인드 연습문제다! 이 사실을 몰라도 문제 내에서 구현이 필요한 연산이 집합합치기/같은집합여부->루트찾기 이고 겹치는 원소가 없는 disjoint 성격이 있기 때문에 쉽게 유니온파인드 사용을 결정할 수

최근에 회사 일이 너무 바빠서 ㅜ 어제는 공부를 못했다 ㅠ...\[백준 오오 전에 푼 \[백준 > O(N)보다 빠른 시간복잡도를 생각하면 O(logn).. O(logn)하면 Tree! 그 중에 각 노드에 구간 혹은 그 구간의 정보를 저장하고 있는 세그먼트 트리를 사용하

피곤🤢\[백준 음 일단 이 문제의 "모든 수는 자신의 한 칸 위에 있는 수보다 크다는 것" 조건을 다음과 같이 생각했다.1\. 위 숫자들은 아래 숫자보다 작음-> 필요시에만 비교하자2\. 가장 밑에 있는 숫자들은 각 라인의 가장 큰 수 -> 여기서 가장 크면 모든 숫

와 이문제 너무 어려워요. 다들 도대체 어떻게 푼거죠,,? 하루를 고민하다가 결국 다른 사람의 풀이방법을 조금 본 문제입니다 ㅠ.....\[백준 문제를 크게 두 부분으로 나눠볼게요.이 단계는 쉬워요. 평소에 동적프로그래밍 문제를 풀듯, 점화식을 찾으면 됩니다.dpn =

\[백준 문제가 전에 풀었던 \[백준 > 따라서, 각자 다른 원소를 가리키고 있는 2개의 포인터를 조작해 해결하는 테크닉인 투포인터를 사용해 해결했습니다!변수들을 다음과 같이 사용했습니다.start: 구간 내 가장 앞의 원소를 가리킴end: 구간의 마지막 원소 뒤를 가

\[백준 사실 소수를 구하는 부분을 제외하고는 \[백준 > 일단 소수를 구하는 방법입니다. 처음엔 이 방법을 생각도 못하고 코드를 짜서 당연히 주어진 시간을 초과했습니다 ㅋ,,이는 수학에서 소수를 찾는 효율적인 방법이에요!알고리즘은 다음과 같습니다.위의 과정을 반복하면

😆😆\[백준 \[백준 > 위 문제와 같이 집합합치기/같은집합여부 연산만으로 해결가능한 문제죠? 유니온파인드를 사용했습니다! 도시들 간의 연결 정보를 받고 "1"이면 두 도시를 merge하는 연산을 진행했습니다. 그리고 여행경로의 첫번째 도시의 루트를 저장해두고, 뒤

2020년 마지막날에도 문제풀이,,,🔥 신난다 ~\[백준 아주아주 대표적인 다익스트라 알고리즘 문제입니다!다익스트라 알고리즘은 그래프의 한 정점에서 시작해 다른 정점들로의 최단거리를 구하는 알고리즘입니다. 다음 방법으로 최단거리 탐색을 진행합니다~step1. 아직 방

\[백준 문제이름에서도 알 수 있듯, 플로이드 와샬 연습문제입니다. 플로이드 와살 알고리즘이란, V개의 정점과 거리가 주어졌을 때, 모든 정점 쌍 사이의 거리를 계산하는 알고리즘입니다!플로이드 와샬 알고리즘은 dp를 기반으로 구현할 수 있습니다. 최단경로 탐색 시 사용

\[백준 "모든 컴퓨터를 연결하는데 필요한 최소비용"는 최소스패닝트리(Minimum Spanning Tree)의 간선 합을 구하라는 뜻이죠?(최소스패닝트리에 대한 간단한 설명은 풀이방법 하단을 참고해주세요) 저는 이 문제를 해결하기 위해 최소스패닝트리를 크루스칼 알고리

\[백준 문제 이름이나 내용에서 바로 알 수 있듯 LCA로 푸는 문제입니다! 최소공통조상이란, 두 정점 u,v가 있을 때 u이거나 u의 조상이면서 동시에 v이거나 v의 조상인 노드들 중 가장 깊은 노드를 뜻합니다~문제 풀이는 두 단계로 구성되어 있습니다!쉽죠??\*\*

\[백준 아무런 알고리즘, 테크닉을 사용하지 않고 문제를 푼다고 생각해봅시다. O(QN)의 시간복잡도를 갖겠네요! 시간제한인 1초를 쉽게 넘기겠죠? 이 문제를 해결하기 위해 일부 함수 결과를 미리 테이블에 저장하는 전처리 과정을 구현했습니다!이렇게 전처리 과정을 통해

\[백준 곰곰~히 생각해보면 그리디 알고리즘으로 해결할 수 있는 문제입니다. 당장 눈 앞의 이익만 좇는 방법이 그리디 알고리즘이죠? 이 문제도 새로운 콘센트를 꽂아야 할 때 앞으로 가장 오랫동안 사용되지 않을 콘센트를 골라 뽑으면 되는 눈 앞의 이익만 좇는 방법입니다

\[백준 이 문제도 잘~ 생각해보면 그리디 알고리즘으로 해결가능한 문제죠? 한 강의실을 사용하는 수업 간의 텀을 짧게 해주면 됩니다! 그럼 최소의 강의실로 모든 수업을 들을 수 있죠~코드의 흐름은 다음과 같습니다.강의실 배정 시에는 다음 케이스들이 존재합니다!아직 아무

\[백준 아주 간단한 DFS 문제입니다! "아주 간단한"이라고 한 이유는 간선이 오직 하나이거나 없기 때문이죠 ! 특정 채널을 싫어하는 사람은 다수일 수 있으나, 채널을 바꾸기 위해 일어나는 사람은 가장 어린 사람 한 명이기 때문에 가장 어린 한 사람만 저장 및 고려하

\[백준 보자마자 최단거리! 다익스트라! 까지 생각나는 문제입니다. 근데 일반적인 다익스트라와 달리 돌아오는 거리까지 고려해야하죠? 따라서, y도시 -> x도시 -> y도시 == (y도시 -> x도시) + (x도시 -> y도시) 값을 구해야합니다!x는 하나로 고정되어

풀고보니 쉬운데 풀이방법을 꽤 길게 고민했던 문제다!\[백준 큰틀은 그리디와 유니온파인드이다!그리디 방식으로 가장 큰 너비의 다리를 순차적으로 가져와 그 사이를 이어준다.(다리 너비 값을 내림차순으로 우선순위를 갖는 우선순위큐를 사용) 다리를 둘 때마다 c와 v가 같은

\[백준 가지치기도 할 수 없는 완전탐색 문제입니다! N의 최대값이 20이기 때문에 완탐으로 문제를 해결해도 되겠죠~? dfs를 사용해 모든 케이스를 탐색했습니다. 매번 sum이라는 부분수열의 합 값을 전달해 sum == s를 만족하면 카운트하는 방식입니다.

\[백준 이름처럼 트리를 이용하면 해결할 수 있는 문제다! 일단 각 노드에 자식 노드를 저장한다. 입력된 잘린 노드(removedNode)가 자식이라면 그 자식을 children 리스트에서 제거 한 뒤 완전탐색(BFS)을 통해 리프노드를 카운트했다!간과한 점들 때문에

\[백준 두가지 풀이방법으로 접근했었다. 둘 다 BFS를 사용한다는 공통점이 있었지만, 첫번째 방법은 table정보를 2차원 배열 그대로 저장했었다. 당연히 메모리초과가 났다 ^0^이걸 어떻게 메모리를 줄일 수 있을까.. 고민했다! 모든 움직인 케이스를 가지고 있었야하

\[백준 매번 구간합, 평균을 구하면 당연히 시간초과가 뜨겠죠? 그래서 구간합 배열을 사용했습니다! sumTabler 값의 의미는 sumTable1 부터 sumTabler 까지 밝기의 합입니다. 이 구간합 배열을 이용해 구간 평균 밝기를 원타임에 구할 수 있습니다~ 쉬

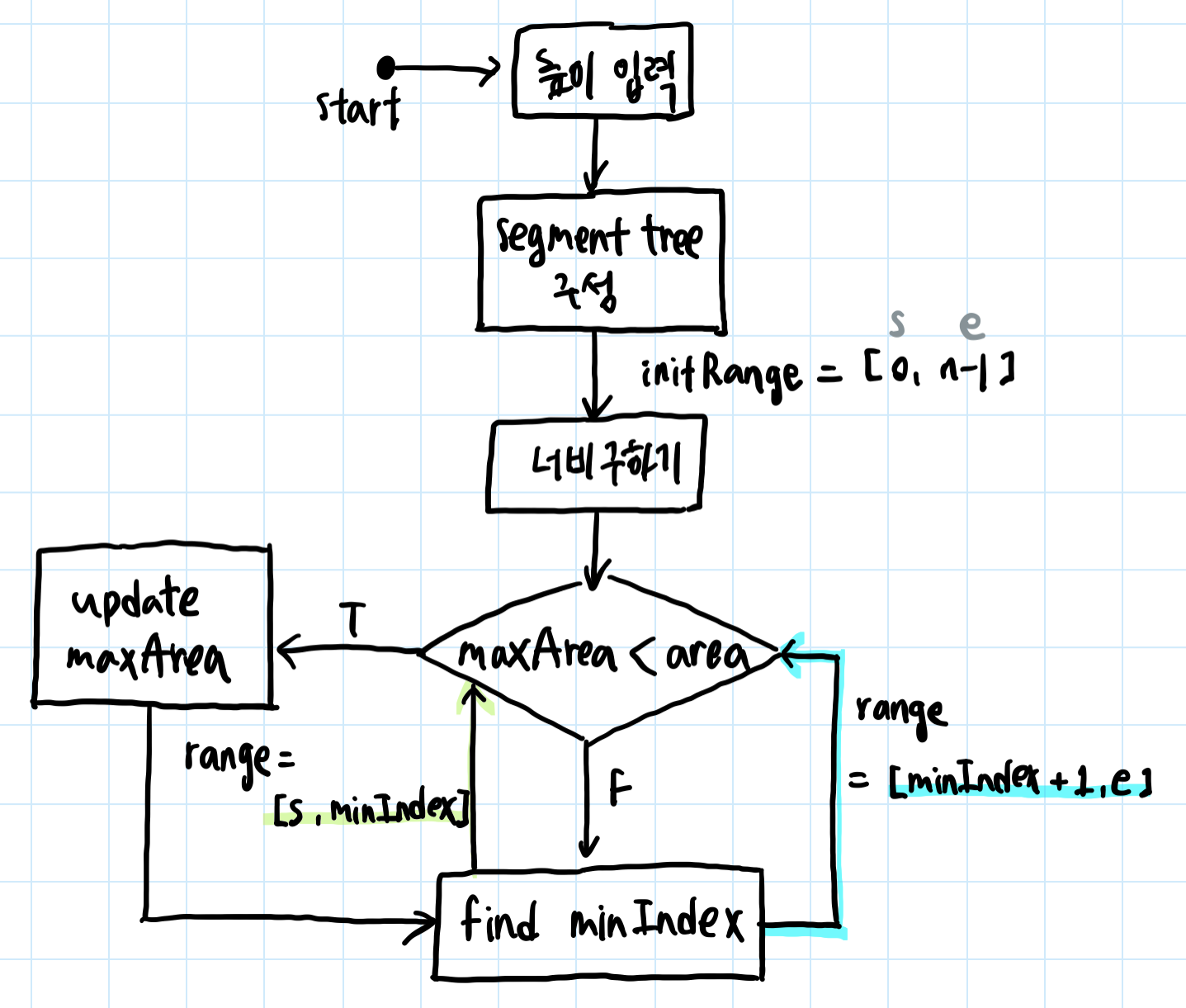
와 진짜 너무 어렵다; 이 문제 뻥 조금 보태서 100번은 본거같은데 매번 너무어렵네~ 얼렁뚱땅 풀기~하고 넘겨버렸는데 오늘은 제대로 풀었다!!!!!!!!! 머리에 쥐날거같았지만 뿌듯하다😇 홀홀..\[백준 일단 세그먼트트리랑 분할정복으로 풀었다.세그먼트트리는 구간 내

\[백준 와 분할정복 풀고싶어서 분할정복으로 검색한 문제인데 보자마자 히스토그램 문제가 생각나서 아주 쉽게 문제를 풀 수 있었다...!!!큰 흐름은 히스토그램과 아아아아주 똑같다. 조금 다른 부분이 있다면 sum(Ai, ..., Aj)를 세그먼트트리를 사용하지 않고 구

\[백준 분할정복 문제다! 사각형의 크기가 2 2가 될때까지 계속 사등분하면 된다. 2 2가 되었을 때 해당 사각형의 (0, 0) (0, 1), (1, 0), (1, 1)를 r, c와 비교하고 count를 늘린다. 단, 모든 케이스에 대해 진행하면 시간초과가 발생하

얼떨결에 풀어버린 문제;\[백준 사실 이 문제말고 가장 긴 증가하는 부분 수열2를 풀라고했다. 채점하니까 시간초과가 떳고 N 범위가 더 작은 문제가 있길래 제출해봤는데 맞아버렸다;우선순위큐를 사용했다. 가장 긴 증가하는 부분 수열이기 때문에 처음원소부터 마지막 원소까지

\[백준 N의 범위를 보고 완점탐색이 가능한 문제라고 생각했습니다! 그리고 가지치기가 중요하다고 생각했어요. 그래서 DFS를 사용하되, 비효율적인 경로를 차단하는 백트래킹을 사용해 문제를 해결했습니다! (비효율적인 경로 == 이미 단순하지 않은 경로)라고 생각해서 결과

와 굉장히 어려웠다\[백준 어려운 문제였다. 세그먼트 트리를 사용해 문제를 해결했는데, 세그먼트트리를 사용해야한다고 생각하는 과정도 어려웠고 시간초과가 나서 그걸 해결하는것도 힘들었다 -0-일단, 세그먼트트리 아이디어를 얻은 과정은 다음과 같다. 이 문제는 dp로도 풀

\[백준 스도쿠 풀이방법을 떠올려 봤을 때 바로 백트래킹이라는 생각이 들었다. 초등학생, 중학생 때 스도쿠를 풀 땐 몰랐지만 그때도 백트래킹을 머리로 하며 풀었던 거였다..!백트래킹이라는 풀이방법까지는 쉽게 접근했는데 이걸 매번 특정 칸이 속하는 행, 열, 박스에 없는

\[백준 주어진 조건들을 보고 바로 백트래킹을 활용하는 문제라고 생각했다. 일반적인 백트래킹 문제 풀이와 같이 갈 수 있는 경로라면 해당 경로를 왔음을 어딘가에 저장하고 다시돌아와서는 그 표시를 되돌려놨다. 보통 백트래킹 문제에서는 map 내의 각 위치에 대해서 vis

\[백준 같은 위원회 내 모든 사람(정점) 사이의 거리를 계산해야 하기 때문에 플로이드 와샬을 사용했습니다. 문제 풀이의 큰 흐름은 다음과 같습니다!입력(입력과 동시에 관계가 있는 사람들 사이의 거리를 1로 설정)모든 구성원 간의 거리를 계산(플로이드와샬 이용)같은 구

\[백준 이 문제는 읽는데 이미 푼 문제인줄 알았습니다.. 혹시 풀었나 확인까지 했어요. 풀고보니 저에 푼 \[백준 \`\`\`import java.util.\*;public class BOJ1916 {}class Bus { public int dest; p

\[백준 슈퍼컴퓨터부터 다른 컴퓨터까지의 최소 시간은 다익스트라를 이용해 구할 수 있다. 근데 이 문제에서는 최소 시간이 아니라 그 최소 시간을 보장하는 "경로"에 대해 묻고있다. 즉, 다익스트라 알고리즘을 통해 사용한 경로를 묻고있다. 이 경로를 어떻게 구할까 생각해

\[Leetcode 이 풀이는 해당 문제의 Discuss를 참고했다. 총 두 가지 방법을 남기고자 한다.생각하기는 쉽지 않지만, 생각하면 쉬운 방법이다. 배열 내 모든 원소의 합을 구하고 그걸 3으로 나누었을 때 경우에 따라 진행한다.sum % 3 == 0 👉 그 값

\[백준 결국 패스하긴 했지만 그 전에 잘못된 방법을 시도했었다. 그 잘못된 풀이부터 쭉- 남기고자 한다.일단, 이동할 수 있는 조건은 두 위치 사이의 거리가 1000이하인 경우이다.첫번째 시도한 방법은 Greedy 스러운 방법이었다. 이동 시 해당 위치에서 가장 가깝

\[백준 풀이 방법이 두 가지이다! 두 방법 모두 작성하고자 한다.간단한 수학식을 이용한 방법이다. 초기값이자 최대 생명력이 방을 통과할 때마다 바뀌는데, 그 차이를 diff라는 변수에 저장했다. 예를 들어,3 31 1 202 3 101 3 100이런 입력이 들어온다면

\[백준 일단 가장 작은 좋은수열을 구해야하기 때문에 1, 2, 3을 순서대롤 붙이는 dfs 방식을 생각했다. 그리고 수열의 부분수열이 나쁜수열이면 거기서 더 연장한 수열은 당연히 나쁜수열이기 때문에 부분수열을 이용해 가지치기를 했다! 좋은 수열인지 확인하는 부분은 한

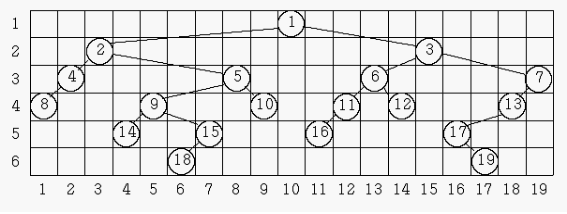
\[백준 트리문제다! 문제에 주어진 아래 그림을 보면서 이리저리 생각해봤다.왼쪽으로 쭉~ 들어가 가장 왼쪽에 있는 노드부터 찾아야 겠다는 생각을 했다. 그러다보니 중위순회가 생각이 났다. 중위순회로 노드들은 방문하니 각 노드에 col index를 매길 수 있었다. 그리

\[백준 너비우선탐색을 이용했다. 비버 굴로 이동할 수 있는 최소 시간을 구해야하기 때문에 깊이우선탐색보다 너비우선탐색을 이용하는게 맞다고 생각했다.물이 확장(확장된 부분을 큐에 넣름)하는 걸 먼저하고, 고슴도치가 이동할 수 있는 곳(비워진 곳으로만 이동가능)을 큐에

\[백준 탈출까지 걸리는 최소시간을 묻기 때문에 너비우선탐색을 이용했습니다! 지금까지 다룬 다른 문제들과 달리 level이 추가되었는데요, 이차원으로 풀던 문제를 삼차원으로 바꾸면 됩니다! 기존엔 dy, dx만 가지고 풀 수 있었지만, 이 문제에서는 dl이라는 변수도

\[벡준 이 풀이방법의 아이디어는 각 날에 풀 문제를 고르자 이다. 그럼 그 날 풀 수 있는 문제들을 알고 있어야 하는데 이를 위해서는 마지막날 부터 진행하는게 수월하다고 생각했다. 왜냐하면 마지막날부터 진행하면 지나온 날과 해당 날이 마감일인 과제들을 자료구조에 넣으

\[백준 개인적으로 재미있는 문제였다! 아래, 왼쪽으로만 움직이는 게 아니니까 DP는 쓸 수 없었다. 완전탐색으로 풀어야하나.. 생각했었다. (0, 0) 부터 (n - 1, n - 1)까지의 최소 거리라고 생각해봤다. 그러니까 다익스트라가 생각났다! 각 위치를 하나의

\[백준 계속 주어진 범위에 다른 값을 가진게 있으면 4등분하면 되는 문제다. 이렇게 작은 문제로 나눠 해결하는 방법을 분할정복이라고 한다! 주어진 범위 내 값들이 같은지 다른지를 쉽게 판단하기 위해 값들을 boolean 타입으로 저장했다. 그리고 nor 연산을 진행해

\[백준 이분탐색 문제였다. 왼쪽값(start)는 k가 될 수 없는 수 중 가장 큰 수로 계속 갱신해 나가고 오른쪽값(end)는 최소 k로 계속 갱신해 나갔다. 문제에 1 ≤ 금액 ≤ 10000 이렇게 되어있어서 처음에 end를 10000로 설정했는데 N이 최대 100

\[백준 최소 비용을 구해야하고, 두 마을로 구성해야 하기 때문에 Greedy + Union Find 로 해결할 수 있다고 생각했다! 모든 길이 없는 상태(모두 다른 마을)에서 비용이 작은 길부터 확인을 진행했다. 만약 두 집이 다른 마을에 있다면 길을 추가해 같은 마

\[백준 처음에는 BFS인가 싶었다. 근데 그렇게 풀자니 괄호처리가 곤란했다; 그래서 생각난게 DP였다. 식을 그대로 갖고있는 게 아니라 계산된 값과 값 사이의 사칙연산을 진행하는거다. 예를 들어서, 길이가 5인 5-연산을 진행한다면, 5 = 1 + 4 = 2 + 3임

\[백준 모든 도시 사이의 거리를 구해야하는 문제라 플로이드 와샬 알고리즘을 이용해 해결했다. 교통수단을 입력받을 때부터 내일로를 이용한 경우, 그렇지 않은 경우를 구분했다. 내일로를 이용하는 경우, 교통수단의 타입과 가격을 getPriceWithPass 메소드로 전달

\[백준 음 보자마자 풀이방법이 떠오른 문제는 아니다. 처음엔 중앙값의 의미를 생각해서 두개씩 추가할때 그 케이스를 나눠서 생각해봤다. 추가되는 두 값을 valueA, valueB라고 하겠다.valueA < mid && valueB < mid👉 n(mid보

\[백준 괄호 관련 문제랑 비슷했다. 이런 규칙을 가진 문제의 경우, 스택으로 해결할 수 있다. 스택을 사용하는건 어렵지 않았지만 문자열을 다루는게 조금 까다로웠다; keyword를 뽑아오는 함수와 오른쪽 꺽쇠 인덱스를 찾는 함수를 따로 구현해 문제를 해결했다!

\[백준 문제를 읽고 \[백준 > \`\`\`class Solution3745 {}class Stock implements Comparable { int index; int price;}

\[백준 그 학생이 자기 키 순서를 알기 위해선 본인보다 (큰 학생의 수) + (작은 학생의 수) 가 n - 1이어 한다. 그래서 큰 학생의 수, 작은 학생의 수를 구할 방법을 생각했다. 큰 한생의 수는 바로 플로이드와샬을 사용하면 되겠다고 생각했다. 근데 작은 학생의

최대공약수(GCD)두 자연수의 공통된 약수 중 가장 큰 수최소공배수(LCM)두 자연수의 공통된 배수 중 가장 작은 수최대공약수1\. 2 - min(a, b) 수를 차례로 넣어 확인\-> O(n)2\. 유클리드 호제법2개의 자연수 a, b (a > b)r = a % b

소팅 알고리즘 중 시간복잡도가 O(n²)인 알고리즘들을 정리하려고 한다!모든 코드는 오름차순 sorting 케이스이고 leetcode - sortColors에 제출해 정답을 얻은 코드이다!선택정렬. 현재 위치에 들어갈 값(선택)을 찾아 정렬처음(index = 0)부터

소팅 알고리즘 중 시간복잡도가 O(nlogn)인 알고리즘들을 정리하려고 한다!정확도는 leetcode - Sort an Array 제출을 통해 확인했다. (코드들은 모두 오름차순 정렬 코드이다)합병정렬. Divide & Conquer 방식으로 설계된 알고리즘으로, 입력

문제링크 백준 #3197. 백조의 호수 풀이방법 어렵지만 재미있는 문제였다! 원래는 풀이 #1으로 풀었는데, 다른 풀이를 보다가 재미있는 풀이방법을 봐서 그 방법으로도 구현해봤다. 풀이 #1 처음에는 BFS 문제인가? 싶었다. 근데 문제를 다시보니 백조가 만나는 시간이

문제링크 백준 #2343. 기타 레슨 풀이방법 전에 풀었던 이진탐색문제와 아주 비슷하게 생겨서 보자마자 이진탐색을 이용하면 되겠다고 생각했다. 즉, begin, end 값을 최초에 설정해두고 툭툭 값을 던져보면서 그 범위를 반으로 나눠나가는 방식을 이용했다. N과 레슨

오늘은 부분수열의 합이라는 문제를 풀었다. 문제링크 #1182. 부분수열의 합 풀이방법 해시태그를 보면 알 수 있듯이, 완전탐색을 이용해 풀었다. 이유는 N의 범위에 있는데, 1 <= N <= 20이기 때문에 2^20, 대략 백만번이기 때문에 완탐으로도 충분!! (대

\[Leetcode LRU Cache 안드로이드 개발 중 종종 들은 키워드이다. LRU 알고리즘은 페이징 교체 알고리즘 중 하나인데, 가장 최근에 쓰이지 않은 페이지를 교체하는 알고리즘이다. 이 알고리즘을 적용한 캐시가 LRU 캐시이다!페이징 교체 알고리즘을 공부한 적

\[백준 신기한 문제다! 벽을 한 번만 부술 수 있는데 이걸 어디에 어떻게 설정해서 알 수 있을까 생각했다. 보통 이차원 배열을 맵으로 사용하는데, 여기서는 한 차원을 더 뒀다. 삼차원 배열을 사용했다. 0j는 한 번도 벽을 부수지 않은 케이스를 다루고 1j는 벽을 한