[Baekjoon] 1005번 ACM Craft.cpp

[백준] 1005번 ACM Craft 문제 링크

거의 처음 시도해 본 골드 3 난이도의 문제이다. 이쯤 되니 기본 알고리즘 분류에 추가로 다른 알고리즘을 접목해야 풀 수 있었다.

· 메인 아이디어

해당 문제는 방향 비순환 그래프를 탐색하는 문제로, 특정 노드가 선행되어야 다음 노드를 방문할 수 있는 규칙을 가지고 있는 문제이다.

방향 비순환 그래프, 노드 순서에 제한이 있는 규칙이라는 것으로 위상 정렬을 떠올릴 수 있다. 사실 필자는 이 위상 정렬을 알지 못해 며칠간 못 풀고 헤매고 있었다. 또다른 알고리즘을 사용해야 할 줄은 몰랐기 때문에..

각설하고, 위상 정렬에 대한 내용은 이 포스트에 정리되어 있고, 위상 정렬과 다이나믹 프로그래밍이 어떤 것인지만 알면 아주 쉽게 풀 수 있는 문제다.

필자는 큐를 이용한 위상 정렬 구현을 하였는데, 큐에서 노드를 꺼내고 자신에게 연결된 진출 간선을 제거하는 과정에 한 가지 작업이 추가된다. 큐에서 꺼낸 노드의 최대 건설 시간이 진출 간선이 가리키는 다음 노드의 최대 건설 시간보다 크다면 값을 갱신해주는 것이다.

예를 들어 아래와 같은 그래프가 문제로 주어졌다고 하자.

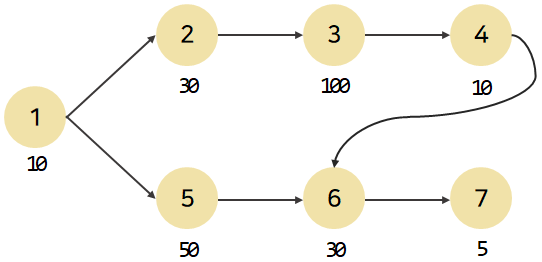
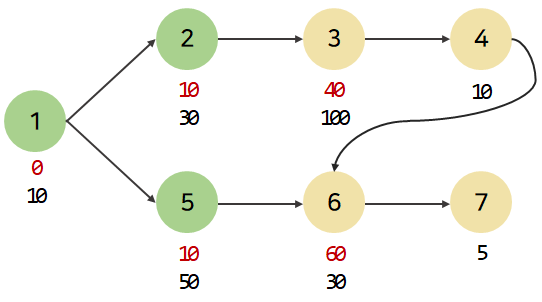
위상 정렬 순서에 따라 1 2 5 번 노드 순서로 방문하면서, 일부 노드에 도달할 때까지 필요한 최대 건설 시간은 다음과 같아진다. 빨간 숫자가 노드에 도달하기 위한 최대 건설 시간, 검정 숫자가 해당 노드를 건설하기 위한 건설 시간이다.

이후 6번 노드는 진입 간선이 존재하기 때문에 3 4번 노드를 먼저 방문한다. 이때, 1 5번 노드를 거치며 갱신된 최대 건설 시간인 60보다 1 2 3 4번 노드를 통해 방문한 건설 시간이 더 크다. 따라서 이 값으로 최대 건설 시간을 갱신해야 한다.

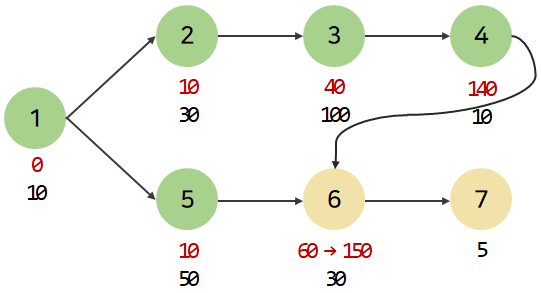
이러한 작업이 위상 정렬 중에 추가된다.

이를 구현한 전체 소스코드는 다음과 같다.

#include <iostream>
#include <vector>
#include <queue>
#define MAX(a, b) ((a > b) ? a : b)

int t, n, k;
int buildings[1001];
int inDegree[1001];
std::vector<int> graph[1001];
std::queue<int> q;

int targetBuilding;
int spendingTime[1001];

void init() {
    for (int index = 0; index <= n; index++) {
        inDegree[index] = 0;
        graph[index].clear();
    }
    while (!q.empty()) {
        q.pop();
    }
}

void trace_prev() {
    for (int count = 1; count <= n; count++) {
        if (inDegree[count] == 0) {
            q.push(count);
        }
    }

    while (!q.empty()) {
        int cur = q.front();
        q.pop();

        if (cur == targetBuilding) {
            break;
        }
        for (auto adj : graph[cur]) {
            if (spendingTime[adj] < spendingTime[cur] + buildings[adj]) {
                spendingTime[adj] = spendingTime[cur] + buildings[adj];
            }
            if ((--inDegree[adj]) == 0) {
                q.push(adj);
            }
        }
    }
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(NULL);
    std::cout.tie(NULL);

    std::cin >> t;
    for (int cases = 0; cases < t; cases++) {
        std::cin >> n >> k;

        init();

        for (int count = 1; count <= n; count++) {
            std::cin >> buildings[count];
            spendingTime[count] = buildings[count];
        }

        int firstBuild, secondBuild;
        for (int count = 1; count <= k; count++) {
            std::cin >> firstBuild >> secondBuild;
            graph[firstBuild].push_back(secondBuild);
            inDegree[secondBuild]++;
        }

        std::cin >> targetBuilding;

        trace_prev();

        std::cout << spendingTime[targetBuilding] << std::endl;
    }
}