[Baekjoon] 9251번 LCS.cpp

[백준] 9251번 LCS 문제 링크

유명한 LCS(Longest Common Subsequence) 최장 공통 부분수열 문제이다. 이름에서 알 수 있는 것처럼 두 개의 문자열이 주어졌을 때 가장 긴 공통 부분 문자열을 만들어내는 것이다.

가장 대중적인 예시인 ACAYKP, CAPCAK로 설명하자면 ACAK가 LCS가 되고, 그 길이는 4이다.

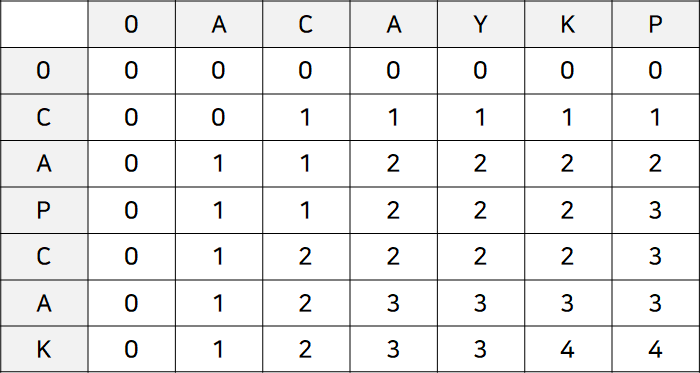
위와 같은 식의 LCS 행렬을 만드는 것이 일반적인 풀이인데, 위 행렬이 의미하는 바는 다음과 같다.

· 두 부분 문자열의 마지막이 같을 때

(2, 1)이라는 좌표는 C와 AC의 LCS를 의미한다. 두 부분 문자열은 C라는 공통 부분 문자열을 가지고 있고, 그 길이는 1이다. 따라서 (2, 1)의 값은 1이다.

다음으로 (2, 3) 좌표를 보자. ACA와 CA의 LCS를 구해야 한다. 이때 두 부분 문자열은 마지막에 온 A라는 공통 문자를 제외하고 AC와 C의 LCS가 1이었다. 이 말은 공통 문자를 발견했을 때 해당 문자를 제외한 부분 문자열 즉, 길이가 1씩 작은 부분 문자열들의 LCS보다 1이 큰 값인 것이다. 이것을 코드로 표현하면 다음과 같다.

if(str1[row] == str2[col]){
	LCS[row + 1][col + 1] = LCS[row][col] + 1

· 두 부분 문자열이 마지막이 다를 때

이번에는 (2, 4)라는 좌표를 주목하자. 이는 CA와 ACAY라는 부분 문자열의 LCS를 값으로 가지는데, 두 부분 문자열의 마지막 문자가 일치하지 않기 때문에 직전의 LCS보다 커지지 않는다.

따라서 해당 부분 문자열에 도달하기 직전 형태의 LCS를 가져온다. 이때 주의할 것은 CA와 ACAY의 직전 형태는 CA와 ACA도 될 수 있고 C와 ACAY도 될 수 있다. 두 경우 중 LCS가 더 큰 값을 해당 부분 문자열들의 LCS로 저장하면 된다. 이를 코드로 표현하면 다음과 같다.

if(str1[row] != str2[col]){
	LCS[row + 1][col + 1] = max(LCS[row + 1][col], LCS[row][col + 1]);

· 인덱스

특정 부분 문자열에 대한 LCS를 저장하는데 실제 코드에서 인덱스 접근을 row + 1, col + 1과 같은 식으로 하는 것에 의문을 가질 수 있다. LCS가 이론적으로 '직전 형태'의 부분 문자열을 가져다 사용하기 때문에 (0, 0)부터 배열을 사용하면 음수의 인덱스를 참조하는 일이 발생하여 첫 행, 열을 비워두고 (1, 1)부터 값을 저장하는 것이 일반적이다.

그렇다면 반복문을 0부터가 아닌 1부터 실행하면 되는 것이 아닌가 할 수 있지만, string 타입은 0번째 인덱스부터 문자를 저장하기 때문에 이를 참조하기 위함이다.

이 모든 것을 적용한 코드 전문은 다음과 같다.

#include <iostream>
#define MAX(a, b) ((a > b) ? a : b)

int LCS[1001][1001] = {0, };

int main(){
    std::ios::sync_with_stdio(false);
    std::cin.tie(NULL);
    std::cout.tie(NULL);

    std::string str1, str2;
    std::cin >> str1 >> str2;
    

    for(int row = 0; row < str1.length(); row++){
        for(int col = 0; col < str2.length(); col++){
            if(str1[row] == str2[col]){
                LCS[row + 1][col + 1] = LCS[row][col] + 1;
            }
            else{
                LCS[row + 1][col + 1] = MAX(LCS[row][col + 1], LCS[row + 1][col]);
            }
        }
    }

    std::cout << LCS[str1.length()][str2.length()];
}