[Algorithm] 문자열 매칭 알고리즘 KMP(Kruth-Morris-Pratt) Algorithm

세동네·2022년 1월 3일

algorithm

[Algorithm] 알고리즘

목록 보기

1/2

[개념]

단순 문자열 비교 알고리즘

긴 문자열에서 작은 문자열을 찾는, 예를 들어 ABCDEF라는 문자열에서 CD라는 문자열을 찾을 때 단순하게 긴 문자열의 첫 번째 인덱스부터 작은 문자열을 하나하나 대조해가는 방법을 떠올릴 수 있다.

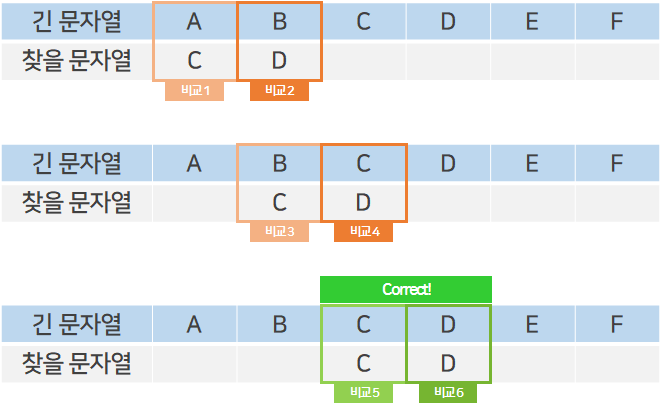
이는 매우 간단하고 쉬운 방법이며, 코드를 공들여 짤 필요가 없어 개발자에게 매우 편한 방법이지만, 그만큼 컴퓨터가 해야 할 일이 늘어나는 탐색 방법이다.

전체 문자열에서 특정 문자열을 찾는 단순 반복 알고리즘은 전체 문자열의 길이 $n$ 을 탐색하면서 특정 문자열의 길이 $m$ 만큼의 비교 연산이 이루어지므로 $O(nm)$ , 극단적인 경우는 $O(n^2)$ 의 처리 시간이 필요하다.

이러한 연산량을 눈에 띄게 줄여줄 수 있는 것이 KMP 알고리즘이다. KMP 알고리즘은 접두사와 접미사 개념을 활용해 반복되는 연산을 얼마나 줄일 수 있는지 판별하여 일부 문자열에서 비교를 생략하여 더 적은 연산량으로 최대 $O(n)$ 까지 시간복잡도를 줄일 수 있는 기법이다.

· 접두사와 접미사

문자열 매칭 알고리즘에서의 접두사와 접미사는 조금 다른 개념이다. 먼저 예시를 보자.

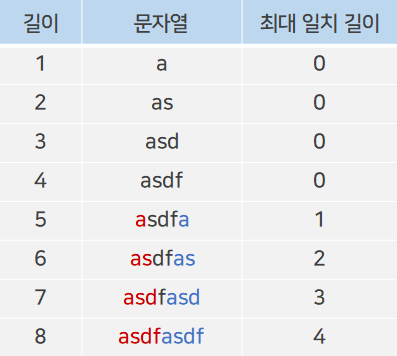
빨간색이 접두사, 파란색이 접미사이다. 문자열에서 첫 번째 글자부터 뒤로 진행하는 Substring이 접두사, 마지막 글자부터 앞으로 진행하는 Substring이 접미사가 되고, 접두사와 접미사가 일치하는 최대 길이를 찾아 이것을 배열로 만든다.

KMP 알고리즘에서 이 최대 일치 길이 배열을 사용할 것이다. 이러한 접두사와 접미사의 최대 일치 길이를 사용했을 때 장점은 전체 문자열과 찾을 문자열을 비교하면서 일치하지 않는 지점이 나왔을 때, 접두사(접미사) 길이 만큼의 비교 연산을 줄일 수 있다는 것이다.

예를 들어 위와 같이 asdfasdf라는 문자열을 전체 문자열에서 찾는다고 해보자. 문자열의 일치를 확인하고 탐색을 잘 진행하다가 마지막 문자에서 불일치를 확인하였다. 기존의 단순 탐색 알고리즘이라면 전체 문자열에서 비교를 시작하는 인덱스를 하나만 옮긴 후 찾을 문자열의 첫 문자부터 다시 비교할 것이다.

이때 위에서 구한 최대 일치 길이 배열을 사용해보자. 불일치가 일어난 지점 이전까지 일치한 부분 문자열 asdfasd의 최대 일치 길이는 3이다.

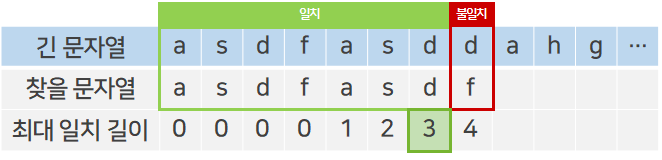
이는 전체 문자열에서 일치한 부분의 마지막 3글자와 찾을 문자열의 앞 3글자가 일치한다는 뜻으로 해석할 수 있다.

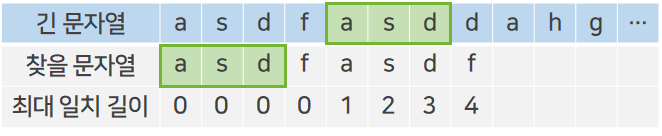
초록색으로 표시된 부분 문자열의 특징이 보이는가? 앞서 최대 일치 길이 배열을 만들 때 표시한 접두사/접미사가 이것과 똑같다. 문자열 탐색 알고리즘에서 접두사/접미사는 이러한 개념으로 사용된다. 이에 따라 일치한다는 것을 확실하게 알고 있는 부분은 비교할 필요가 없다.

따라서 전체 문자열에서 인덱스 하나를 옮긴 b가 아닌 전체 문자열에서 접두사가 다시 나타나는 부분부터 비교를 시작하면 되는 것이다. 첫 a와 다음 접두사가 나타나는 a 사이에 있는 s, d, f부터 시작하는 비교 연산은 생략할 수 있다.

이후 문자열의 일치가 실패했던 지점부터 다시 비교를 시작한다. 하지만 또다시 불일치가 일어났고, 이전까지 일치한 부분 문자열의 최대 일치 길이는 0인 것을 확인할 수 있다.

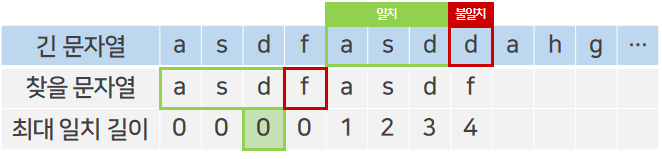
일치 길이가 0이므로 일치한 부분 문자열 asd는 더이상 비교하는 의미가 없는 것이다. 따라서 찾을 문자열의 첫 번째 인덱스부터 다시 비교를 시작한다.

이러한 과정을 거치면 전체 문자열의 첫 인덱스인 a 이후 불일치가 나타난 인덱스까지 sdfasd라는 여섯 문자에서의 비교 연산이 생략됐다는 것을 확인할 수 있다. 단순 문자열 비교 알고리즘보다 현저하게 비교 연산 횟수가 줄어듦을 확인하였다.

[소스코드]

위 내용을 소스코드 알고리즘으로 구현한 것을 살펴보자. 먼저 문자열의 최대 일치 길이 배열을 만들어야 한다.

· 최대 일치 길이 배열 생성

#include <iostream>
#include <vector>
using namespace std;

vector<int> MakeTable(string pattern) {
	int patternSize = pattern.size();
	vector<int> table(patternSize, 0);

	int start = 0;
	for (int end = 1; end < patternSize; end++) {
		while (start > 0 && pattern[start] != pattern[end]) {
			start = table[start - 1];
		}
		if (pattern[start] == pattern[end]) {
			table[end] = ++start;
		}
	}

	return table;
}

cpp의 list는 배열 기반이 아닌 노드 기반 컨테이너이기 때문에 반복자를 사용하게 되어 특정 인덱스에 바로 접근하는 것이 불가능하다. 따라서 배열 형태의 vector 컨테이너를 사용했다. 기본적으로 길이 배열을 모두 0으로 초기화하고 시작한다.

pattern은 최대 일치 길이 배열을 만들 문자열(본문에서는 찾을 문자열), table은 최대 일치 길이 배열이다.

문자열의 길이가 n이라면 첫 번째 인덱스부터 시작하는 1부터 n 길이의 모든 부분 문자열에 대한 길이 배열을 만들어야 한다. start 변수는 접두사, end 변수는 접미사를 담당한다. 접두사는 항상 첫 번째 인덱스부터 시작하기 때문에 접두사의 길이 즉, 불일치한 시점의 start가 가리키는 문자의 위치가 최대 일치 길이가 된다.

while (start > 0 && pattern[start] != pattern[end]) {
	start = table[start - 1];
}

start 위치의 문자와 end 위치의 문자가 다르다면 start를 이전 인덱스로 옮긴다. 이는 같은 문자가 나오거나 start가 첫 인덱스까지 이동할 때까지 반복한다. 이때 접두사 내에서도 일치 패턴이 존재하고, 그것이 table에 저장돼있으므로 그 정보를 가져다 사용하면 더 빠른 비교를 진행할 수 있다.

if (pattern[start] == pattern[end]) {
	table[end] = ++start;
}

start 위치의 문자와 end 위치의 문자가 같다면 접두사, 접미사가 일치하는 것이므로 table에 최대 일치 길이를 업데이트해준다.

위 알고리즘으로 asdfasdf라는 문자열에 대해 다음과 같은 결과를 얻어낼 수 있다.

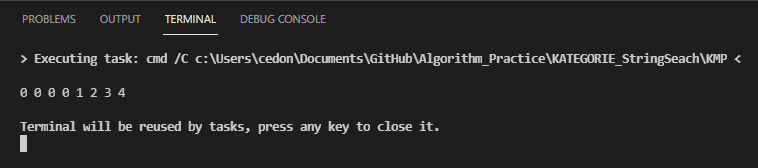
· KMP 알고리즘

vector<int> KMP(string parent, string pattern) {
	int parentSize = parent.size();
	int patternSize = pattern.size();

	vector<int> table = MakeTable(pattern);

	int patternCount = 0;

	vector<int> found_index;
	for (int parentCount = 0; parentCount < parentSize; parentCount++) {
		while (patternCount > 0 && parent[parentCount] != pattern[patternCount]) {
			patternCount = table[patternCount - 1];
		}
		if (parent[parentCount] == pattern[patternCount]) {
			if (patternCount == patternSize - 1) {
				found_index.push_back(parentCount - patternSize + 2);
				patternCount = table[patternCount];
			}
			else {
				patternCount++;
			}
		}
	}
	return found_index;
}

KMP 알고리즘에서 parent은 전체 문자열, pattern은 찾을 문자열이다. 한 문자열 안에서 두 개의 Count를 사용했던 MakeTable 함수와 다르게 parent와 pattern에서 각각의 Count를 사용한다.

while (patternCount > 0 && parent[parentCount] != pattern[patternCount]) {
	patternCount = table[patternCount - 1];
}

불일치 지점이 확인됐으면 찾을 문자열을 세던 Count 위치를 최대 일치 길이 위치로 이동시킨다. 그리고 이동한 위치에서도 불일치한다면 일치하거나 Count가 0이 될 때까지 반복한다.

if (parent[parentCount] == pattern[patternCount]) {
	if (patternCount == patternSize - 1) {
		found_index.push_back(parentCount - patternSize + 2);
		patternCount = table[patternCount];
	}
	else {
		patternCount++;
	}
}

문자가 일치한다면 계속 탐색을 이어가고, 비교하고 있는 길이가 찾을 문자열의 길이와 같아진다면 해당 문자열을 찾은 것이 되므로 찾을 문자열이 전체 문자열의 몇 번째 인덱스에 존재하는지를 저장한다.

이때 찾을 문자열이 전체 문자열에서 발견되는 첫 번째 위치만 반환한다면 여기서 함수를 종료하면 되지만, 우리는 전체 문자열에서 찾을 문자열이 발견되는 모든 위치를 알아낼 것이다. 따라서 일치하는 것이 확실한 접두사 위치까지만 Count를 이동하고 다시 탐색을 시작한다.

불일치의 경우엔 table[patternCount - 1]로 Count에 하나를 뺀 값을 사용했는데 위 경우에서 table[patternCount]로 Count 그 자체의 값을 가져온 이유는 말 그대로 해당 위치가 일치한 것이 확인됐기 때문이다. 불일치가 일어났다면 해당 인덱스의 값을 다시 비교해주어야 하지만 일치했다면 해당 인덱스를 다시 비교할 필요가 없으므로 -1 연산을 해주지 않는다.

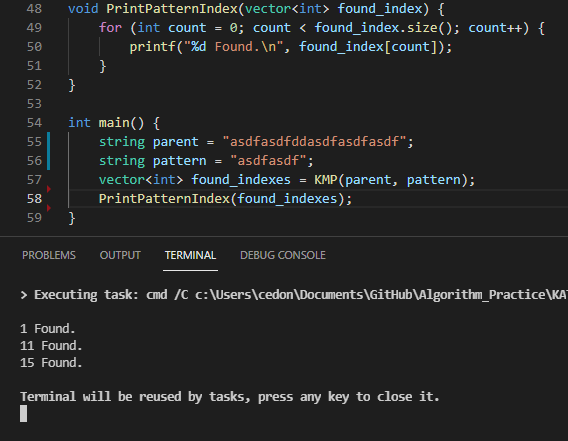
이러한 알고리즘으로 asdfddasdfasdfasdf라는 전체 문자열에서 asdfasdf라는 문자열이 등장하는 모든 위치를 찾는다면 다음과 같은 결과를 얻을 수 있다.

세동네

다음 포스트