이번 게시글에도 대뜸 전체 소스코드를 먼저 공개하고, 기능 단위별로 설명을 이어가겠다.
public class DoubleLinkedList {
DNode head = null;
DNode tail = null;
int size = 0;
DNode findNode(int index) {
//1. 인덱스 음수고, 사이즈보다 크거나 같으면 예외 발생
if (index < 0 || index >= size) {
throw new ArrayIndexOutOfBoundsException();
}
DNode pointer;
int flag = 0;
if (size/2 > index) {
//2. 앞에서 찾기
pointer = head;
flag = 0;
while (flag != index) {
pointer = pointer.right;
++flag;
}
} else {
//3. 뒤에서 찾기
pointer = tail;
flag = size-1;
while (flag != index) {
pointer = pointer.left;
--flag;
}
}
return pointer;
}
Object getData(int index) {
return this.findNode(index).data;
}
boolean isEmpty() {
return size == 0;
}
int size() {
return size;
}
void addLast(Object data) {
this.add(size, data);
}
void addFirst(Object data) {
this.add(0, data);
}
void removeFirst() {
this.remove(0);
}
void removeLast() {
this.remove(size-1);
}
void add(int index, Object data) {
DNode newNode = new DNode();
newNode.data = data;
if (index == 0 || size == index) {
//1. 최초 노드 삽입 or 맨앞 or 맨 뒤에 노드 삽입 시
// 최초 -> index == 0, size == index
// 맨앞 -> index == 0
// 맨뒤 -> size==index
if (this.head == null && this.tail == null) {
this.head = newNode;
this.tail = newNode;
} else if (index == 0) {
newNode.right = this.head;
this.head.left = newNode;
this.head = newNode;
} else {
newNode.left = this.tail;
this.tail.right = newNode;
this.tail = newNode;
}
} else {
//2. 특정 인덱스에 데이터를 삽입하는 경우
DNode foundNode = this.findNode(index);
DNode leftNode = foundNode.left;
//새로운 노드와 찾은 노드의 연결
newNode.right = foundNode;
foundNode.left = newNode;
//새로운 노드와 왼쪽 노드의 연결
newNode.left = leftNode;
leftNode.right = newNode;
}
++size;
}
void remove(int index) {
DNode foundNode = this.findNode(index);
DNode leftNode = foundNode.left;
DNode rightNode = foundNode.right;
if (leftNode != null) {
leftNode.right = rightNode;
}
if (rightNode != null) {
rightNode.left = leftNode;
}
if (index == 0) {
this.head = rightNode;
}
if (index == size-1) {
this.tail = leftNode;
}
foundNode.left = null;
foundNode.right = null;
foundNode.data = null;
--size;
}
@Override
public String toString() {
StringBuilder stringBuilder = new StringBuilder();
DNode pointer = head;
stringBuilder.append("head").append(" -> ");
while (null != pointer) {
stringBuilder.append(pointer.data).append(" -> ");
pointer = pointer.right;
}
stringBuilder.append("null ");
if (null != tail) {
stringBuilder.append(", tail(").append(tail.data).append("), ");
}
pointer = tail;
stringBuilder.append("tail").append(" -> ");
while (null != pointer) {
stringBuilder.append(pointer.data).append(" -> ");
pointer = pointer.left;
}
stringBuilder.append("null");
if (null != head) {
stringBuilder.append(", head(").append(head.data).append(")");
}
return stringBuilder.toString();
}
}
아마 단방향 연결리스트보다 구현 코드가 조금 더 복잡해보일 것이다. 하지만 노드의 구성이 바뀐 점을 고려하고, 원리를 이해하면 구현하기 어렵지 않을 것이다.
오늘 필요한 함수는 아래와 같다.
- 삽입() 함수
- 삭제() 함수
-> 삽입, 삭제 모두 위치에 따라 구현 방식이 다르다.- 탐색() 함수
-> 이분탐색 도입해야함.
1. 삽입() 함수
삽입 방식은 최초 삽입, 맨 앞 삽입, 맨 뒤 삽입, 중간 삽입으로 분류된다. 즉, 4가지 모두에 대응할 수 있는 로직을 짜야한다.
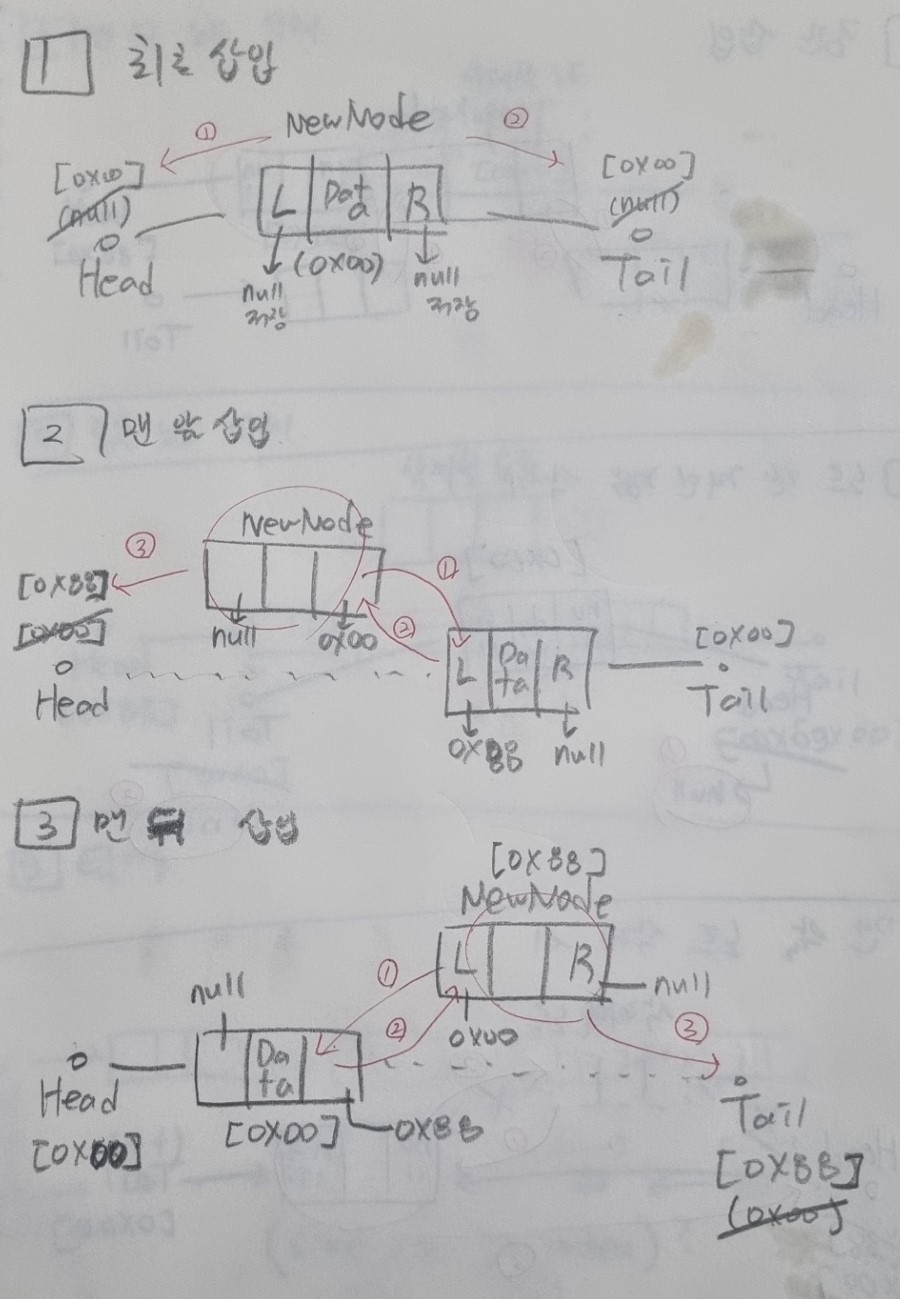
- 최초 삽입 시
초기에 head와 tail은 모두 null 값으로 세팅되어 있을 것이다. 그리고 연결리스트의 size 역시 0 일 것이다. 새로운 노드가 생성되면, head와 tail은 새로운 노드의 주소값을 저장하면 된다.
- 맨 앞 삽입 시
새로 생성된 노드의 right영역에 기존 노드의 주소를 저장한다. 그 후, 기존 노드의 left영역에 새로 생성될 노드의 주소를 저장하면 된다. 마지막으로 head를 새로운 노드의 주소값으로 갱신하면 된다.
- 맨 뒤 삽입 시
새로 생성된 노드의 left영역에 기존 노드의 주소를 저장한다. 그 후, 기존 노드의 right영역에 새로 생성된 노드의 주소를 저장한다. 마지막으로 tail을 새로 생성된 노드의 주소값으로 갱신하면 된다.
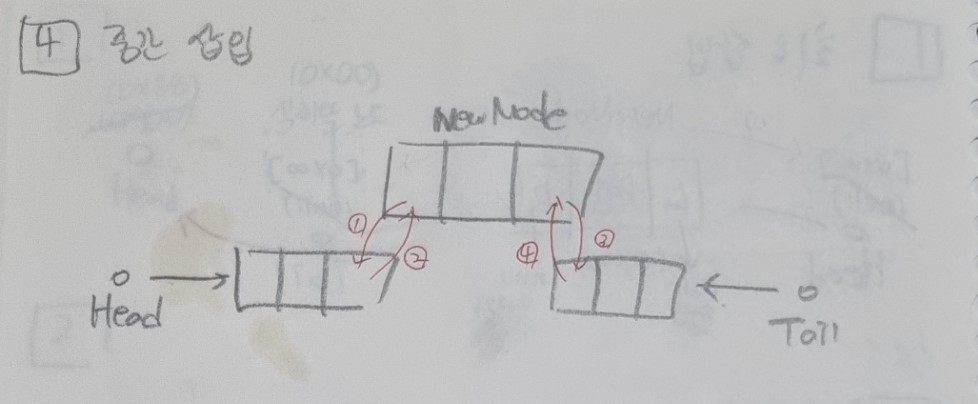
- 중간 삽입 시
새 노드의 left와 right 모두 양쪽 노드의 주소값으로 채운다. 또한 왼쪽 노드의 right는 새로운 노드의 주소값으로, 오른쪽 노드의 left는 새로운 노드의 주소값으로 갱신한다.
구현 코드는 아래와 같다.
void add(int index, Object data) {
DNode newNode = new DNode();
newNode.data = data;
if (index == 0 || size == index) {
//1. 최초 노드 삽입 or 맨앞 or 맨 뒤에 노드 삽입 시
// 최초 -> index == 0, size == index
// 맨앞 -> index == 0
// 맨뒤 -> size==index
if (this.head == null && this.tail == null) {
this.head = newNode;
this.tail = newNode;
} else if (index == 0) {
newNode.right = this.head;
this.head.left = newNode;
this.head = newNode;
} else {
newNode.left = this.tail;
this.tail.right = newNode;
this.tail = newNode;
}
} else {
//2. (중간삽입)특정 인덱스에 데이터를 삽입하는 경우
DNode foundNode = this.findNode(index);
DNode leftNode = foundNode.left;
//새로운 노드와 찾은 노드의 연결
newNode.right = foundNode;
foundNode.left = newNode;
//새로운 노드와 왼쪽 노드의 연결
newNode.left = leftNode;
leftNode.right = newNode;
}
++size;
}2. 삭제() 함수
노드 삭제 역시 4가지 방식이 존재한다.
노드가 한 개 남은 경우 삭제 방식, 맨 앞 노드를 삭제하는 경우, 맨 뒤 노드를 삭제하는 경우, 중간 노드를 삭제하는 경우로 분류된다. 하나의 함수 안에 각각의 방식에 모두 대응할 수 있는 로직을 짜야한다.
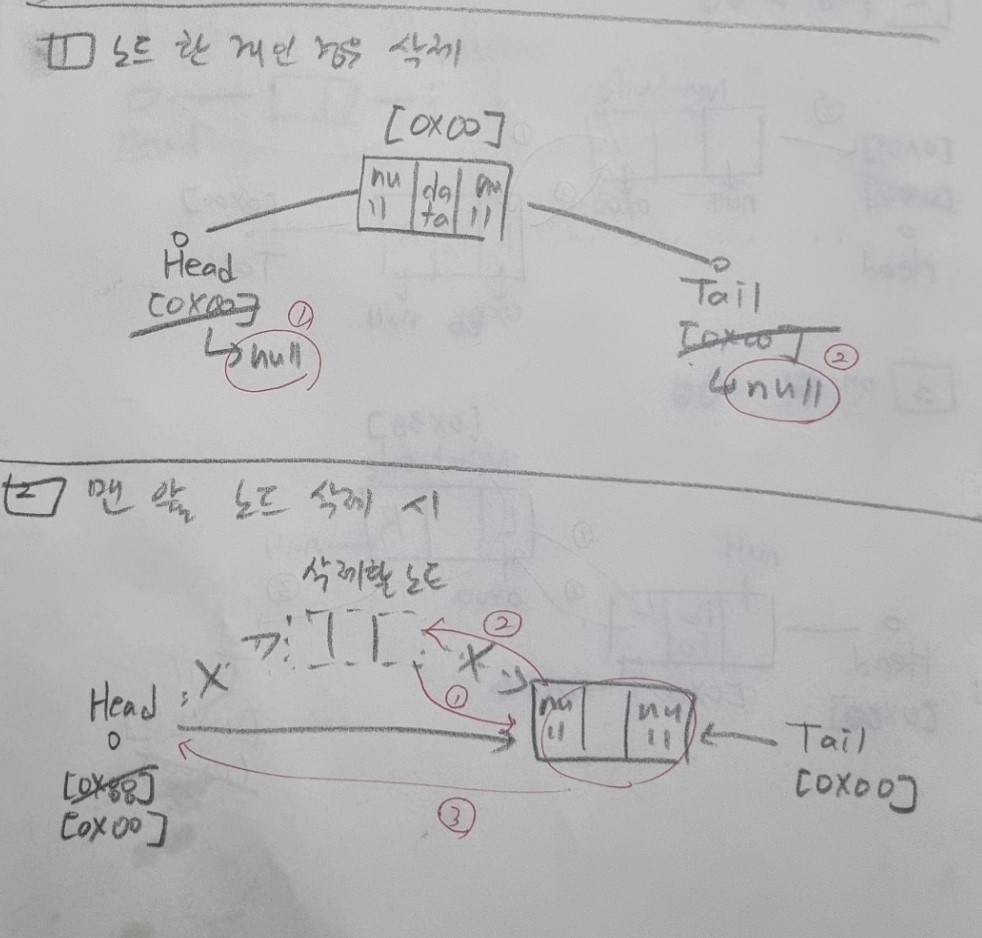
- 노드가 한 개 남은 경우 삭제방식
제일 단순하다. 그저 head와 tail을 null로 초기화시키면 된다. 삭제 될 노드는 가비지 컬렉터가 수거해간다.
- 맨 앞 노드 삭제
삭제할 노드의 다음 노드의 left 영역을 null로 초기화 시킨다. 그리고 head를 삭제할 노드의 다음 노드의 주소로 갱신한다. 그리고 삭제시킬 노드의 left, data, right 영역 모두 null로 초기화 시킨다.
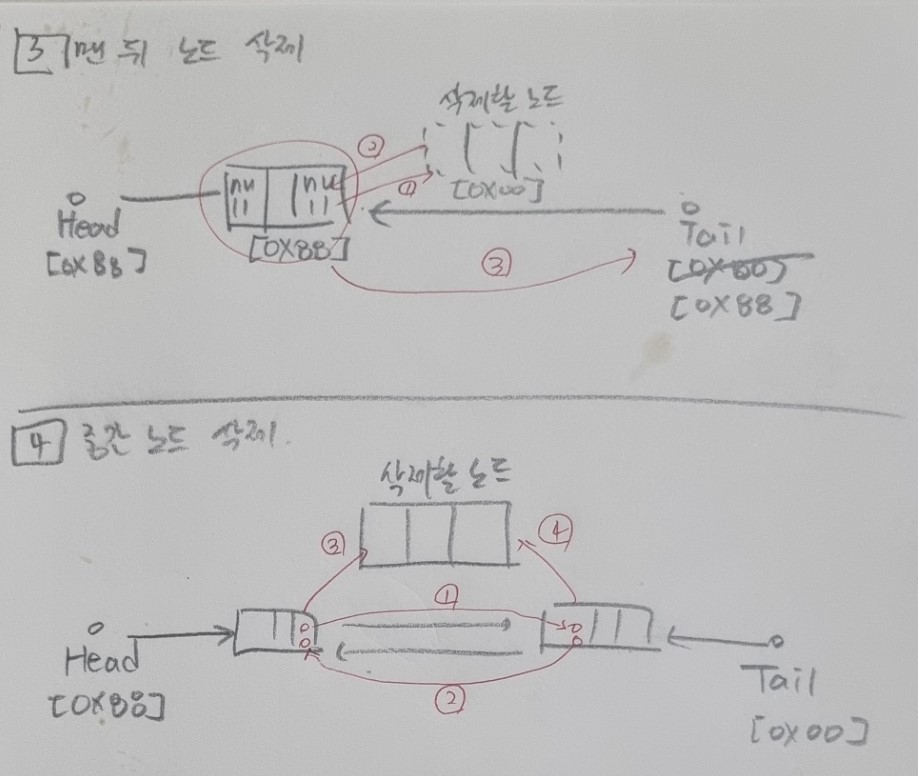
- 맨 뒤 노드 삭제
삭제할 노드의 이전 노드의 right 영역을 null로 초기화 시킨다. 그리고 tail을 삭제할 노드의 이전 노드의 주소값으로 갱신한다. 마지막으로 삭제시킬 노드의 left, data, right영역 모두 null로 초기화 시킨다.
- 중간 노드 삭제
삭제할 노드의 이전 노드의 right 영역을 삭제할 노드의 이후 노드의 주소값으로 대체한다. 마찬가지로 삭제할 노드의 이후 노드의 left영역은 삭제할 노드의 이전 노드의 주소값으로 대체한다. 그리고 삭제할 노드의 data, left, right 영역 모두 null로 대체시킨다.
위의 4가지 방식은 다양한 조건의 제어문으로 처리해야한다.
void remove(int index) {
DNode foundNode = this.findNode(index);
DNode leftNode = foundNode.left;
DNode rightNode = foundNode.right;
if (leftNode != null) {
//scope 1. 좌측 노드가 존재할 경우
leftNode.right = rightNode;
}
if (rightNode != null) {
//scope 2. 우측 노드가 존재할 경우
rightNode.left = leftNode;
}
if (index == 0) {
//scope 3. 첫번째 노드를 삭제할 경우
this.head = rightNode;
}
if (index == size-1) {
//scope 4. 마지막 노드를 삭제할 경우
this.tail = leftNode;
}
foundNode.left = null;
foundNode.right = null;
foundNode.data = null;
--size;
}아...이게 도대체 무슨 🐶소리냐고 여쭤보실 수 있다.
그래서 여러 가지 예시를 들어 설명하겠다.
- 첫 번째 노드를 삭제할 경우
- scope 2, 3 동작
- 원소가 한 개 남은 상태에서 삭제를 진행할 경우
- scope 3, 4 동작
- 중간 노드를 삭제할 경우
- scope 1, 2 동작
- 마지막 노드를 삭제할 경우
- scope 1, 4 동작
3. 탐색() 함수
양방향 연결리스트엔 tail이라는 새로운 친구가 등장한다. 우리가 찾고자 하는 인덱스가 중간값보다 작으면 head부터 탐색하고, 중간값보다 크면 tail부터 탐색하면 된다. 즉 이분탐색만으로 이 함수를 간단하게 구현할 수 있다.

어떤 조건문에 들어가느냐에 따라 포인터에 할당될 값이 달라진다. 만약 head부터 출발하면, 우측으로 한 칸씩 이동하면서 우리가 찾을 원소를 가져오면 된다. tail부터 출발하면, 좌측으로 한 칸씩 이동하면서 우리가 찾을 원소를 가져오면 된다.
DNode findNode(int index) {
//1. 인덱스 음수고, 사이즈보다 크거나 같으면 예외 발생
if (index < 0 || index >= size) {
throw new ArrayIndexOutOfBoundsException();
}
DNode pointer;
int flag = 0;
if (size/2 > index) {
//2. 앞에서 찾기
pointer = head;
flag = 0;
while (flag != index) {
pointer = pointer.right;
++flag;
}
} else {
//3. 뒤에서 찾기
pointer = tail;
flag = size-1;
while (flag != index) {
pointer = pointer.left;
--flag;
}
}
return pointer;
}4. 정리
이렇게 양방향 연결리스트 구현을 마무리하도록 하겠다. 노드가 어떻게 바뀌고, left-right 영역에 어떤 값이 들어오는지 이해한다면 양방향도 무리없이 이해할 수 있다. 다음 챕터는 Stack이다.
