1. 개요
A국은 인구 5만명의 소규모 국가이다. A국의 대통령 선거는 단 10개의 선거함만 있으면 처리 가능하다.
하지만 어느 순간, 이민자들이 폭증하면서 인구가 10만명으로 증가했다.
그러면 10개의 선거함이 더 필요한데, A국은 선거함을 수입해와야한다.
선거위원장은 이렇게 생각했다. '그냥 기존의 선거함을 개조해서, 선거함을 미술용 물통처럼 유연하게 늘리면 되지않나?'

그렇다. 기존의 방식은 '배열'이고, 선거함을 개조한 방식은 '연결리스트'이다.
배열은 프로그래머가 선언한 공간만큼만 사용할 수 있고,
연결리스트는 굳이 공간을 선언하지 않아도 데이터 저장공간이 더 필요하면 유연하게 공간을 늘릴 수 있다.
선거함 1개가 5000명 분의 투표용지만을 담았다면, 새로운 방식은 5000명 이상의 투표용지를 담을 수 있는 것이다.
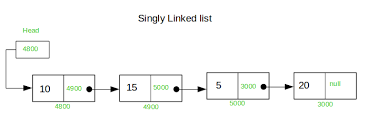
이렇듯 입력될 데이터의 양이 불확실할 때, 유연하게 데이터를 담을 수 있도록 만든 자료구조가 연결리스트이다.
연결리스트는 현재 노드의 next라는 고유 영역에 다음 노드의 주소를 저장하기 때문에, 두 데이터의 물리적 위치가 달라도
서로가 연결되어 있음을 인지할 수 있다.
2. 연결리스트 VS 배열
- 배열
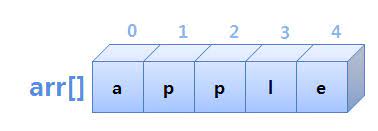
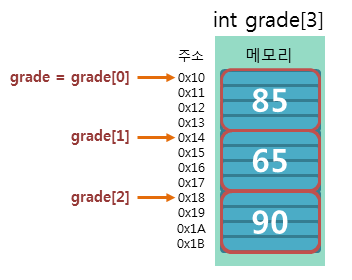
앞서 말했든 배열은 초기에 프로그래머가 선언한 만큼의 공간을 사용할 수 있다.
장점은 논리적 저장순서와 물리적 저장순서가 일치한다는 것이다. 따라서 인덱스를 사용해서
특정 원소에 직접 접근할 수 있다(Random Access: 비순차적 접근).
7번째 원소를 찾기 위해, 처음부터 일일히 탐색할 필요가 없다는 것이다.
그래서 탐색에 필요한 시간은 O(1) 이다. 하지만 삽입, 삭제 시에는 O(N)의 시간이
필요하다. 그 이유는 특정 위치에 삽입, 삭제를 하기 위해선 원소를 한 칸씩 뒤로 혹은 앞으로
이동시켜야한다. 따라서 오버헤드가 크다고 말할 수 있다.
또한 불필요한 공간이 생겨 메모리가 낭비될 수 있다.
int[] arr = new int[10];
arr[1] = 10;
arr[2] = 30;
//남은 공간 낭비됨.만약 개발자가 배열의 크기를 10으로 선언했는데, 넣어놓은 데이터가 2개 밖에 없다면?
자원 낭비이다.
- 연결리스트
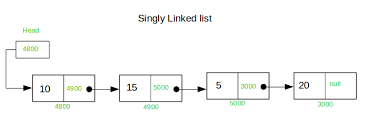
연결리스트는 물리적 저장순서와 논리적 저장순서가 일치하지 않는다.
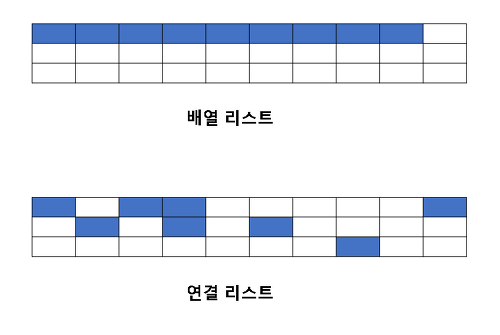
배열이 선언되면 메모리의 특정 영역을 연속적으로 사용하고,
연결리스트는 빈 공간을 사용하여 데이터와 다음 데이터의 주소를 저장한다.
따라서 한 노드가
다음 노드의 주소정보를 갖고 있어야 연결될 수 있는 구조이다. 복잡해 보이지만, 저장공간이
유연하게 증가 및 감소시킬 수 있다. 하지만 비순차적 접근이 불가능하다.
인덱스가 없기 때문에, 특정 원소를 검색할 때 무조건 첫 노드부터 접근해야한다.
그래서 탐색 시간은 O(N)이 소모된다.
하지만 맨 앞, 혹은 맨 뒤의 원소를 삽입&삭제 할 때는 O(1)이다. 탐색할 필요가 없기 때문이다.
그러나 중간에 있는 특정 노드를 삽입&삭제 할 땐 O(N)의 시간이 소모될 수 있다.
탐색이 필요하기 때문이다.
그러나 삽입&삭제 시에 배열보다 큰 장점이 있는데, 저장 공간을 재배치 시킬 필요가 없다는 것이다.
배열은 삽입&삭제 시에 원소를 한 칸씩 앞 혹은 뒤로 미뤄야하는데,
연결리스트는 그럴 필요가 없다.
장점이 압도적으로 많아보이지만, 연결리스트도 치명적인 단점이 있다.
바로 '단편화' 이슈이다. 각 노드마다 메모리 공간을 비순차적으로 할당된다. 새로운 프로세스가 만약 메모리에 올라오려 할 때, 공간이 충분함에도 불구하고 중구난방하게 데이터가 할당되어 있기 때문에 비집고 들어올 공간이 없게 된다.
3. 수행시간 비교
Array
- 탐색 O(1)
- 삽입 O(n)
- 삭제 O(n)
LinkedList
- 탐색 O(n)
- 삽입 [맨 앞, 혹은 맨 뒤 삽입 시]O(1), [탐색을 통한 중간 삽입]O(N)
- 삭제 [맨 앞, 혹은 맨 뒤 삭제 시]O(1), [탐색을 통한 중간노드 삭제]O(N)
