시간 복잡도 (Time Complexity)
특정 크기의 입력을 기준으로 할 때 필요한 연산의 횟수
최선의 경우 (Best Case)
최적의 입력을 한 상태에서, 작업을 완료하는 데 가장 연산 횟수가 적은 경우
최악의 경우 (Worst Case)
최악의 입력을 한 상태에서, 작업을 완료하는 데 가장 연산 횟수가 많은 경우
평균의 경우 (Average Case)
여러 경우의 수를 고려하여, 총 연산 횟수를 계산하고 시행 횟수로 나눈 경우
평균의 경우와 최악의 경우가 가장 많이 활용
알고리즘이 복잡해질수록 평균을 구하는 것이 어렵기 때문에, 최악의 경우로 알고리즘 성능을 파악
빅오 표기법 (Big-O notation)
빅오 표기법(Big-O notation)은 복잡도를 나타내는 점근 표기법이며 알고리즘 효율성을 상한선 기준으로 표기
최악의 경우를 고려하는 데 가장 좋은 표기법
빅오 표기법의 특징
1. 상수항 무시
빅오 표기법은 n이 충분히 크다고 가정, 알고리즘의 효율성은 n의 크기에 영향을 받으므로 상수항은 무시
O(2n)은 O(n)으로 간주
2. 영향력 없는 항 무시
빅오 표기법은 n의 크기에 영향을 받으므로 가장 영향력이 큰 항 이외에 영향력이 없는 항은 무시
O(n^2 + 2n + 1)은 O(n^2)으로 간주
시간 복잡도와 빅오 표기법
시간 복잡도는 특정 크기의 입력(n)을 기준으로 실행하는 연산의 횟수
즉, 연산의 횟수를 세는 것
그러면 알고리즘이 실행될 때의 모든 연산의 횟수를 세는가?
NO , 알고리즘에서 핵심이 되는 연산의 횟수만 세면 된다.
시간 복잡도와 그 예시
| 복잡도 | 소요시간 | 예시 |
|---|---|---|
| O(1) | 상수 시간 | 스택에서 Push, Pop |
| O(log n) | 로그 시간 | 이진트리 |
| O(n) | 직선적 시간 | for 문 |
| O(n log n) | 선형 로그 시간 | 퀵 정렬(quick sort), 병합 정렬(merge sort), 힙 정렬(heap sort) |
| O(n^2) | 2차 시간 | 이중 for 문, 삽입 정렬(insertion sort), 거품 정렬(bubble sort), 선택 정렬(selection sort) |
| O(C^n) | 지수 시간 | 피보나치 수열 |
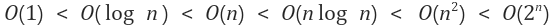
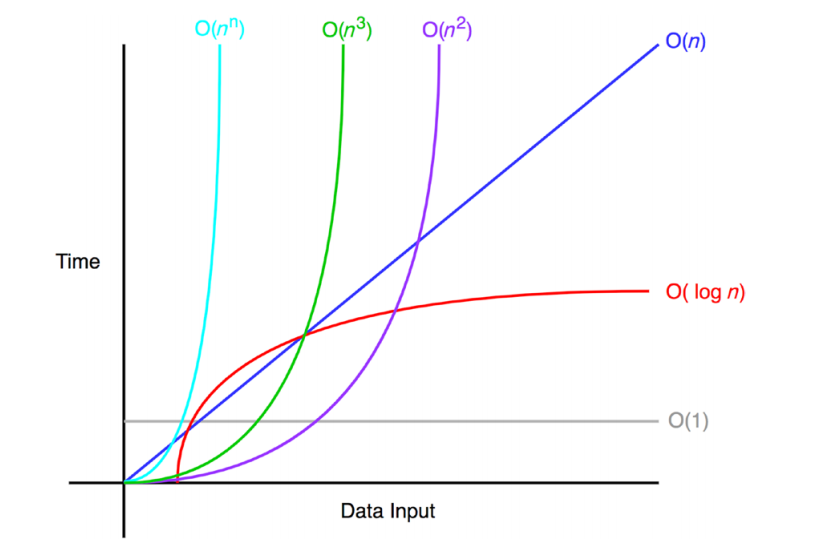
상수함수 < 로그함수 < 선형함수 < 다항함수 < 지수함수
왼쪽에서 오른쪽으로 갈수록 성능이 떨어지기 때문에, 시간 복잡도가 좋지 않은 알고리즘임
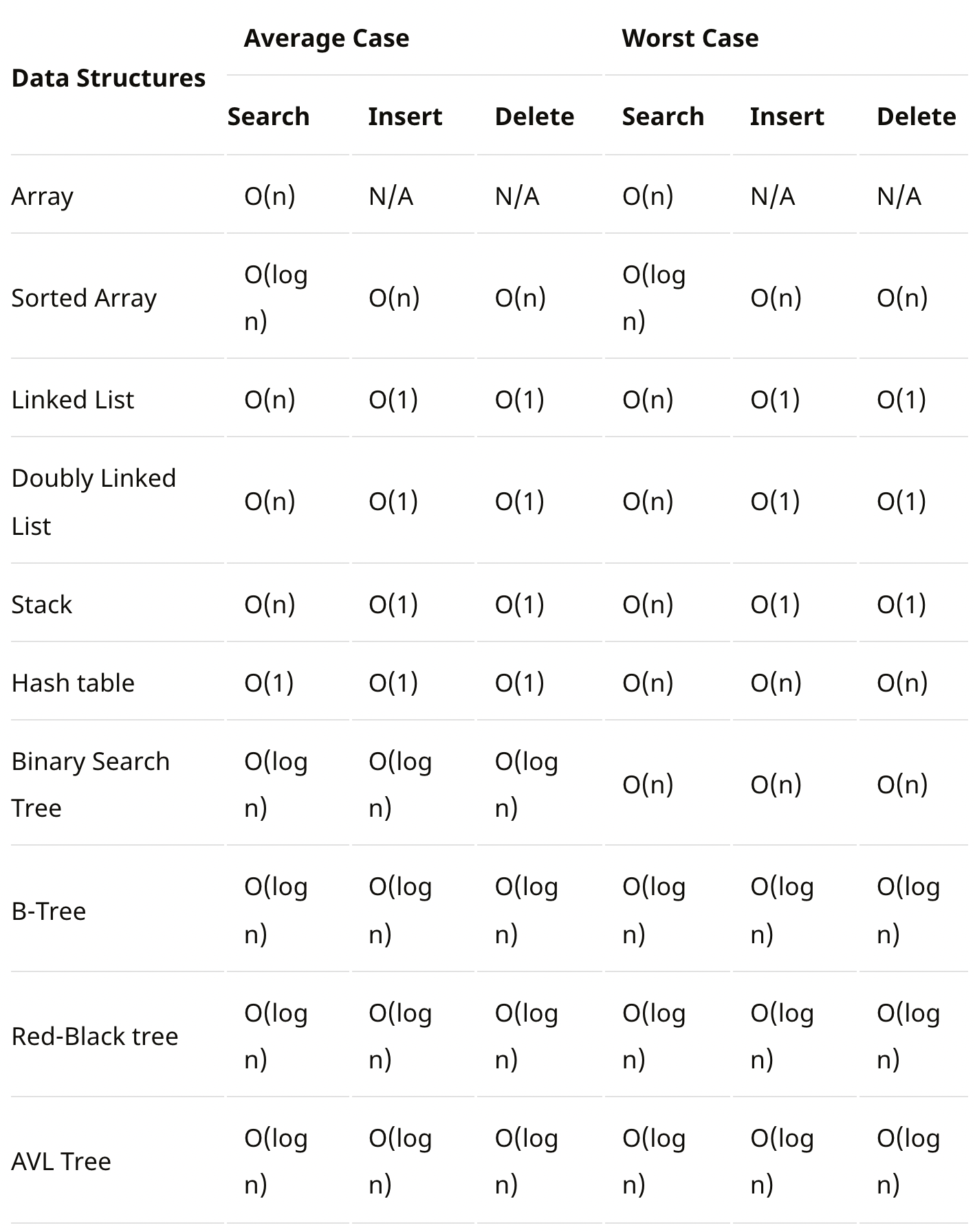
Big-O 표기법으로 나타낸 자료구조의 시간 복잡도
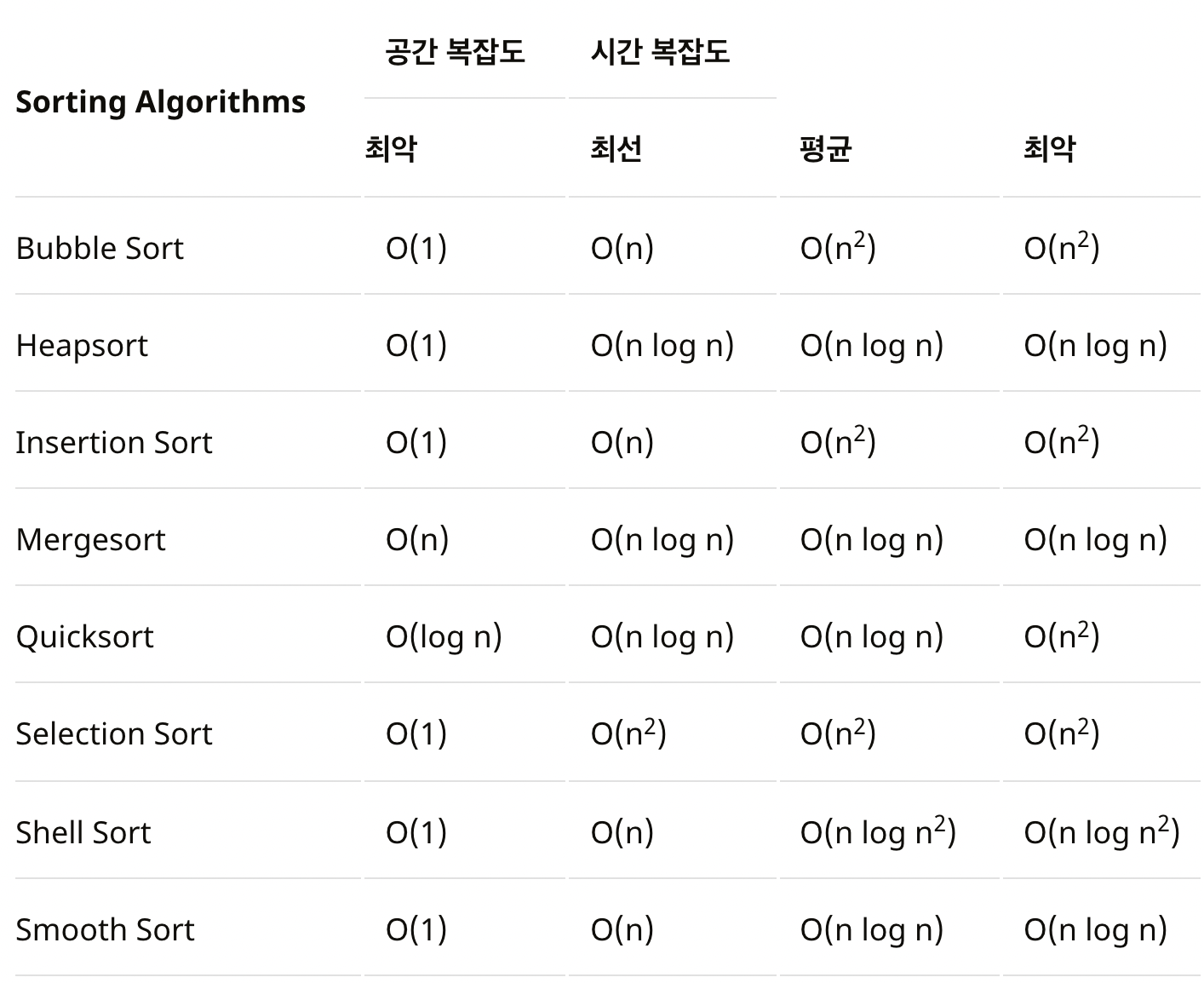
Big-O 표기법으로 나타낸 정렬 알고리즘의 시간 복잡도