주절주절 서론
최근에 알고리즘 문제풀이로 다음의 문제집에서 랜덤하게 분류와 문제를 뽑아서 풀고있다. 이번에 뽑은 문제는 백준1976-여행가자인데, Disjoint Set으로 문제가 분류되어 있었다. 분리 집합 / 서로소 집합이라고 하니 어느정도 감은 오지만 매번 무작정 문제만 푸는 것이 더이상 발전이 없다고 생각해서 이참에 알고리즘 기법을 한 번 정리하고 넘어가려고 한다 !
Disjoint Set
분리 집합 혹은 서로소 집합이라고 하는 Disjoint Set이란 다음과 같다.
서로 중복되지 않는 부분 집합들로 나누어지는 원소들로 이루어진 집합을 말한다. 각 원소들에 대한 정보, 즉 값이나 부분 집합에 대한 정보를 저장 및 조작할 수 있는 자료구조를 말한다.
내가 이해하기 편한 나의 워딩으로 바꿔보면 교집합이 없는 부분 집합이라고 생각하면 될 것 같다 !
Union Find
그렇다면 Disjoint Set과 나란히 붙어다니는 Union Find는 Disjoint Set을 표현하기 위한 자료구조 / 알고리즘이다.
배열, 링크드 리스트, 해쉬, 트리 등 다양한 자료구조로 구현할 수 있다. 아래에서는 요구되는 각 연산과 구현 원리에 대해서 설명할 것이고, 대표적으로 배열과 트리로 구현하는 방법에 대해서 설명할 것이다.
연산 종류
-
make_set(x) : 초기화 연산, x 스스로만이 집합의 원소이고, 스스로가 집합의 구분자이게 설정한다.
-
union(x, y) : 병합 연산, x가 속한 집합과 y가 속한 집합을 합친다. 이 때, 합친 집합의 구분자는 상황에 적절하게 설정한다.
-
find(x) : 찾기 연산, x가 속한 집합의 구분자를 반환한다. 즉, x가 속한 집합을 찾는 연산이다.
구현
배열로 구현하기
Array[i]의 value가 i가 속합 집합의 대표 번호를 의미하게끔 구현한다.- make_set(x) : size만큼의 array를 할당한 후, array[i] = i로 초기화 하여, 스스로가 집합의 대표번호로 설정되게끔 구현한다.
- union(x,y) : 기본적으로 x를 병합된 집합의 대표번호가 된다고 설정하면, 배열을 순회하며 집합번호, 즉 value가 y이면 x로 바꿔준다. if(array[i]==y) array[i]=x
- find(x) : x가 속한 집합의 대표번호는 array[i]에 저장된 value이므로 이를 반환한다.
-
트리로 구현하기
하나의 트리가 같은 집합을 의미하게끔 구현한다. 또한 트리의 루트 노드가 집합의 대표 번호를 의미하게 된다.
- make_set(x) : size만큼의 루트 노드를 생성하고 value를 설정한다.
- union(x,y) : 기본적으로 x를 병합된 집합의 대표번호가 된다고 설정하면, x와 y 각각 부모를 따라 올라가며 루트 노드를 찾는다. 이 때, x와 y의 루트 노드가 다르다면 y의 루트 노드를 x의 루트 노드의 자손으로 설정하여 트리를 병합한다.
- find(x) : x 노드부터 시작하여 부모를 따라 올라가며 루트 노드를 찾아 반환한다.
💡 이 때, find 연산에 있어서는 배열이 O(1)으로 효율적인 시간 복잡도를 갖는다. 하지만 union의 시간 복잡도는 O(N)이 되는데, 트리 구조의 경우 find도 union도 트리의 깊이만큼의 시간 복잡도를 갖게 된다. 트리 자손의 차수를 높이거나, 균형을 맞추는 등의 방법으로 트리의 높이를 낮출 수 있다면 size가 커지면 커질수록 트리가 효율적인 구조일 것이다.
-
코드
트리 구조를 배열로 표현하여 구현한 코드이다. 즉 array[i]에 저장된 value가 트리에서 i 노드의 부모 노드를 의미하게 된다.
public class UnionFind {
int[] root;
UnionFind(int size){
this.root = new int[size];
for(int i=0; i<size; i++){
root[i] = i;
}
}
int find(int x){
if(root[x] == x) return x;
else return find(root[x]);
}
void union(int x, int y){
x = find(x);
y = find(y);
root[y] = x;
}
}최적화
위의 코드는 위에서 언급한 트리의 높이를 낮추기 위한 방법들이 적용되지 않았다. 그러므로 아래의 그림과 같이 n개의 노드에 대해서 높이 n인 극적이로 비효율적인 트리가 나올 수도 있다.

따라서 최적화 과정을 포함하면 좋은데, 아래와 같이 find와 union 각 연산 과정에서 진행할 수 있는 2가지 최적화 방법이 존재한다.
-
find 최적화
: find 경로 단축을 위해서 find 연산으로 거쳐간 모든 경로 노드의 부모를 루트 노드로 설정해준다. 아래와 같이 모든 경로 노드들은 루트 노드의 자손이 되므로 루트 노드를 한 단계만을 거쳐 찾을 수 있게 된다.
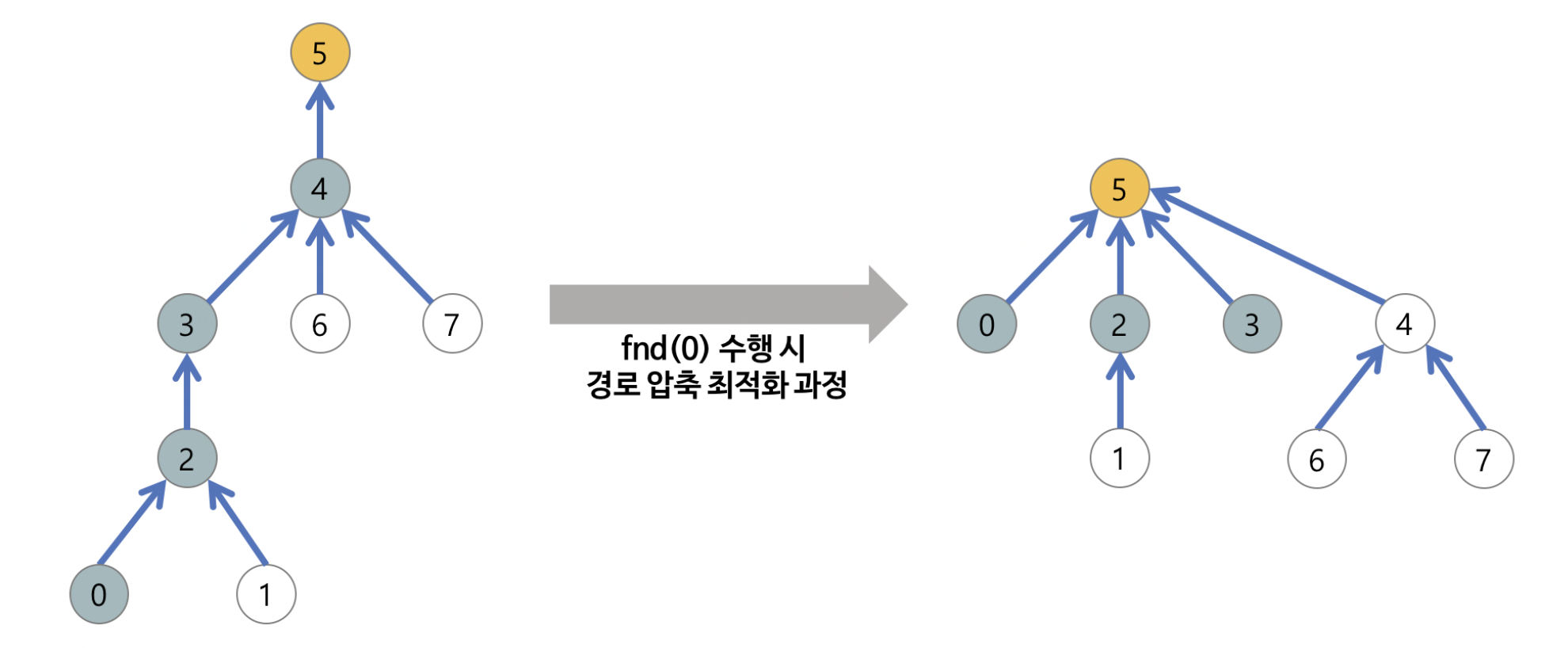
-
union 최적화
: 트리의 높이를 저장하고, 트리 병합시에 높이가 더 낮은 트리를 더 높은 트리의 아래에 넣는 방법으로 병합한다. 이렇게 병합하면 트리의 높이가 더 높아지지 않지만, 반대로 한다면 트리의 깊이가 더 깊어지는 것을 아래의 그림으로 확인할 수 있다.
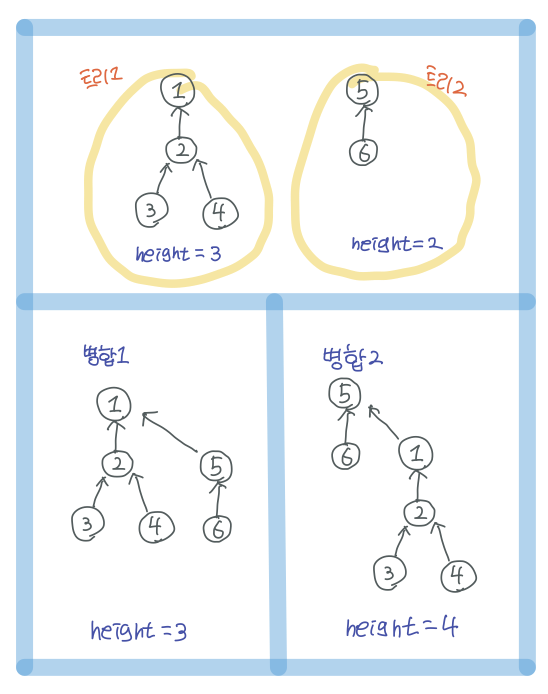
최적화를 반영한 코드
public class UnionFindOpt {
int[] root;
int[] height;
UnionFindOpt(int size){
this.root = new int[size];
this.height = new int[size];
for(int i=0; i<size; i++){
root[i] = i;
height[i] = 0;
}
}
int find(int x){
if(root[x] == x) return x;
else return root[x] = find(root[x]);
}
void union(int x, int y){
x = find(x);
y = find(y);
root[y] = x;
if(x == y)
return;
if(height[x] < height[y]) root[x] = y;
else {
root[y] = x;
if(height[x] == height[y]) height[x]++;
}
}
}