어제 풀려고 시도한 문제는 프로그래머스 위클리 챌린지 3주차 퍼즐 조각 맞추기 문제이다.
사실 3주차 문제가 올라오고 한 번 문제를 슥 읽어뒀었다. 조각은 BFS로 찾아내고.. 그 다음엔 어쩌지 조금씩 고민을 하고 있었는데, 비슷한 문제가 있다고 해서 카카오 기출인 자물쇠와 열쇠(포스팅 보러가기)를 먼저 풀어보았다. 그냥 이차원 배열을 이용하는 빡구현 같았다.
도움 요청 ❤️🔥
어쨌든 비슷한 문제를 먼저 풀고 어제 이 문제를 풀려고 시도하는데 계속 6개 테케가 통과를 못해서 붙잡고 있다가 결국 포기,, 😭 아래 문제와 풀이방법과 코드를 올려둘테니 ! 그리고 주석도 열심히 달아봤어요 ! 혹시 어디가 문제인지 발견하신 분은 제발제발 댓글 주셔요..
문제 설명
테이블 위에 놓인 퍼즐 조각을 게임 보드의 빈 공간에 적절히 올려놓으려 합니다. 게임 보드와 테이블은 모두 각 칸이 1x1 크기인 정사각 격자 모양입니다. 이때, 다음 규칙에 따라 테이블 위에 놓인 퍼즐 조각을 게임 보드의 빈칸에 채우면 됩니다.
- 조각은 한 번에 하나씩 채워 넣습니다.
- 조각을 회전시킬 수 있습니다.
- 조각을 뒤집을 수는 없습니다.
- 게임 보드에 새로 채워 넣은 퍼즐 조각과 인접한 칸이 비어있으면 안 됩니다.
다음은 퍼즐 조각을 채우는 예시입니다.
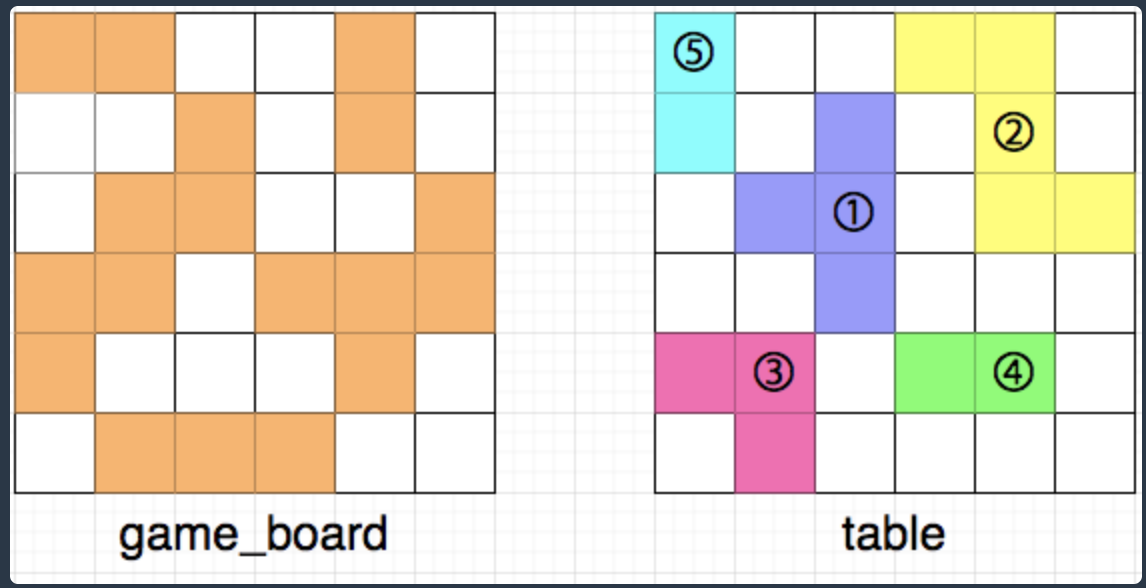
위 그림에서 왼쪽은 현재 게임 보드의 상태를, 오른쪽은 테이블 위에 놓인 퍼즐 조각들을 나타냅니다. 테이블 위에 놓인 퍼즐 조각들 또한 마찬가지로 [상,하,좌,우]로 인접해 붙어있는 경우는 없으며, 흰 칸은 퍼즐이 놓이지 않은 빈 공간을 나타냅니다. 모든 퍼즐 조각은 격자 칸에 딱 맞게 놓여있으며, 격자 칸을 벗어나거나, 걸쳐 있는 등 잘못 놓인 경우는 없습니다.
이때, 아래 그림과 같이 3,4,5번 조각을 격자 칸에 놓으면 규칙에 어긋나므로 불가능한 경우입니다.
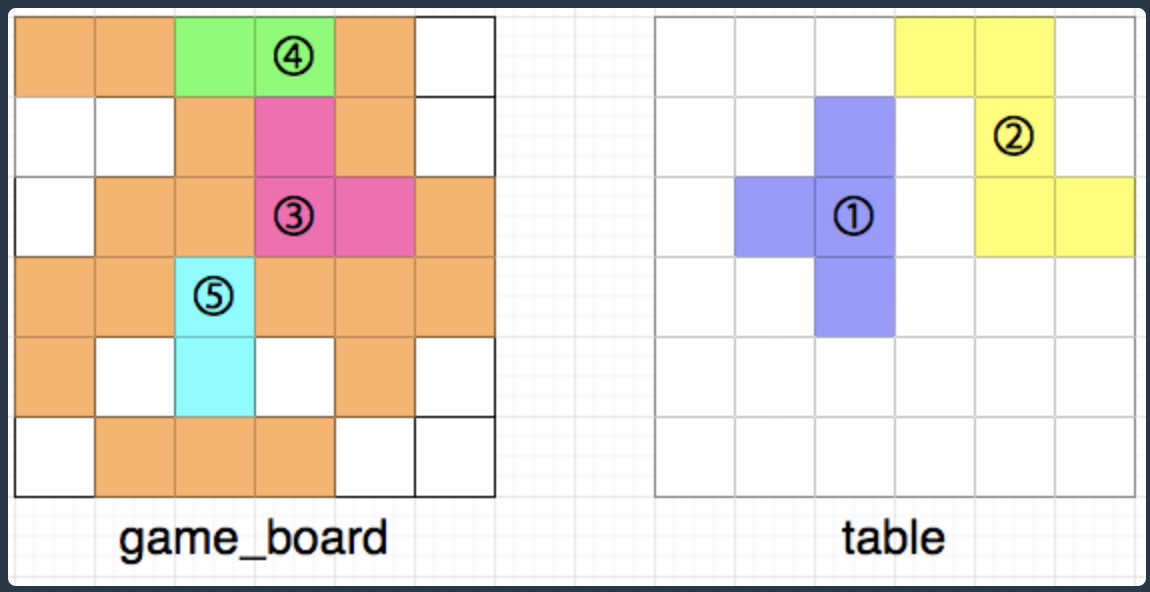
- 3번 조각을 놓고 4번 조각을 놓기 전에 위쪽으로 인접한 칸에 빈칸이 생깁니다.
- 5번 조각의 양 옆으로 인접한 칸에 빈칸이 생깁니다.
다음은 규칙에 맞게 최대한 많은 조각을 게임 보드에 채워 넣은 모습입니다.
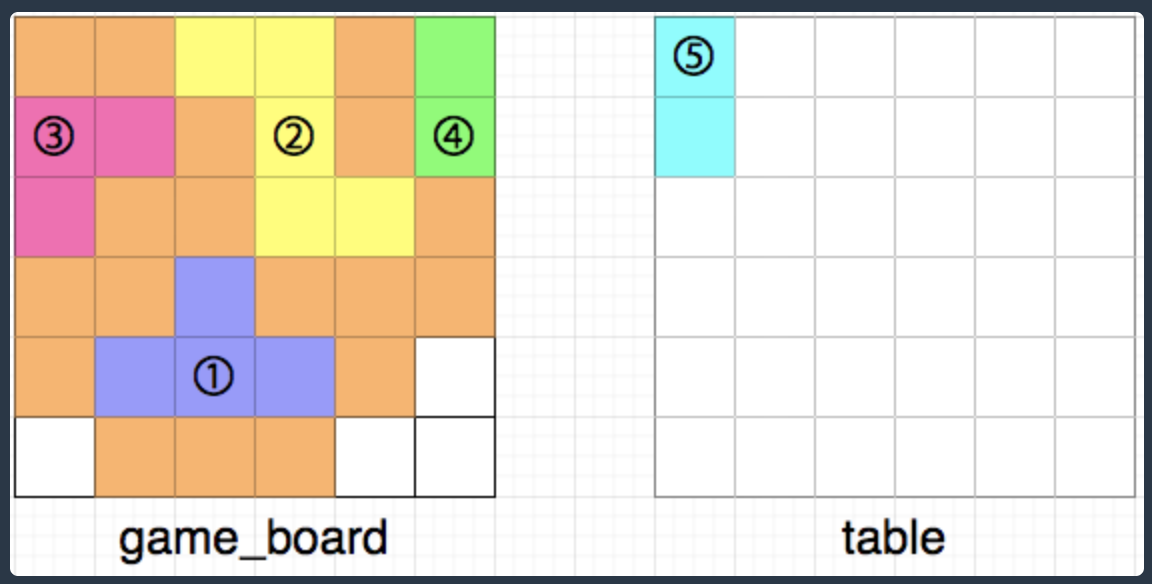
최대한 많은 조각을 채워 넣으면 총 14칸을 채울 수 있습니다.
현재 게임 보드의 상태 game_board, 테이블 위에 놓인 퍼즐 조각의 상태 table이 매개변수로 주어집니다. 규칙에 맞게 최대한 많은 퍼즐 조각을 채워 넣을 경우, 총 몇 칸을 채울 수 있는지 return 하도록 solution 함수를 완성해주세요.
제한 사항
- 3 ≤ game_board의 행 길이 ≤ 50
- game_board의 각 열 길이 = game_board의 행 길이
- 즉, 게임 보드는 정사각 격자 모양입니다.
- game_board의 모든 원소는 0 또는 1입니다.
- 0은 빈칸, 1은 이미 채워진 칸을 나타냅니다.
- 퍼즐 조각이 놓일 빈칸은 1 x 1 크기 정사각형이 최소 1개에서 최대 6개까지 연결된 형태로만 주어집니다.
- table의 행 길이 = game_board의 행 길이
- table의 각 열 길이 = table의 행 길이
- 즉, 테이블은 game_board와 같은 크기의 정사각 격자 모양입니다.
- table의 모든 원소는 0 또는 1입니다.
- 0은 빈칸, 1은 조각이 놓인 칸을 나타냅니다.
- 퍼즐 조각은 1 x 1 크기 정사각형이 최소 1개에서 최대 6개까지 연결된 형태로만 주어집니다.
- game_board에는 반드시 하나 이상의 빈칸이 있습니다.
- table에는 반드시 하나 이상의 블록이 놓여 있습니다.
입출력 예
| game_board | table | result |
|---|---|---|
| [[1,1,0,0,1,0],[0,0,1,0,1,0],[0,1,1,0,0,1],[1,1,0,1,1,1],[1,0,0,0,1,0],[0,1,1,1,0,0]] | [[1,0,0,1,1,0],[1,0,1,0,1,0],[0,1,1,0,1,1],[0,0,1,0,0,0],[1,1,0,1,1,0],[0,1,0,0,0,0]] | 14 |
| [[0,0,0],[1,1,0],[1,1,1]] | [[1,1,1],[1,0,0],[0,0,0]] | 0 |
풀이 방법
블록을 뽑아내자 !
먼저 table 배열을 탐색하면서 각 블록들을 분리해야 했다. 그래서 먼저 블록을 어떤 형태로 저장하고 표현해야 할지를 고민했다. 그러다가 우선 블록을 뽑아내기 위해서 table을 bfs로 탐색하면서 연결된 1들을 탐색하고 table과 같은 사이즈의 배열에 해당 좌표만 1로 변경해줌으로 블록의 모양을 표현해주었다.
또한 그렇게 되면 남는 공간이 많아지고, 그러면 후에 board와 탐색을 진행할 때 효율성이 떨어지기 때문에 행과 열을 탐색하면서 1이 없는 행과 열을 판단하여 블록이 위치하는 컴팩트한 공간을 파악했다.
이처럼 블록의 모양이 저장된 배열, 그리고 블록이 존재하는 공간의 시작과 끝 좌표, 후에 결과값을 도출하는 데에 필요한 차지하는 블록의 칸 수 등등이 필요하기에 Block 클래스를 만들고 관련된 속성과 함수를 분리해주었다.
뽑아낸 블록이 보드에 들어가는지 확인하자 !
우선 블록은 회전이 가능하기 때문에 각 방향에 대해서 아래의 확인 과정을 해주어야 한다. 그러므로 회전하는 함수를 만들어두고 사용하였다. 이 때, 배열만 회전할 것이 아니고, 너비 높이나 배열에서 블록이 위치하는 공간듸 시작과 끝 좌표 등도 바뀌기 때문에 같이 업데이트 해주어야 한다 !
이제 보드의 좌측 상단부터 우측 하단까지 한칸씩 이동하며 블록이 해당 위치에 들어갈 수 있는지 판단을 한다. 이 때 판단 기준은 아래 세 개와 같다.
- 보드와 블록이 모두 0이면 안된다 ! ( 빈 공간이 생기므로 들어갈 수 없다 )
- 보드와 블록이 모두 1이면 안된다 ! ( 들어갈 수 없는 위치이다 )
- 블록의 바로 바깥에 이어지는 0이 있으면 안된다 ! ( 이어진 빈 공간이 모두 채워지지 않은, 즉 인접한 빈 공간이 있는 것이다 )
여기서 1과 2는 보드와 블록이 같은 위치인지 판단해주면 되고, 3번은 블록의 사면 끝에 위치한 0이 있다면 그 바로 바깥 원소가 0인지 확인해주면 된다 !
위의 조건들을 모두 통과해서 딱 맞게 들어갈 수 있다고 판단이 되면 해당 블록은 들어갈 수 있기 때문에 보드의 그 위치를 1로 채워주고, 블록의 칸 수만큼 answer를 증가시켜주었다 !
코드
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
class Solution {
public static int[] dx = {0, 1, 0, -1};
public static int[] dy = {1, 0, -1, 0};
public static class Point{
private int x;
private int y;
Point(int x, int y){
this.x = x;
this.y = y;
}
public void plusX() {
this.x++;
}
public void plusY() {
this.y++;
}
public void minusX(){
this.x--;
}
public void minusY(){
this.y--;
}
}
public static class Block{
private int[][] block; // 블록 배열, table, board와 사이즈 동일
private int count; // 블록의 개수
private int size; // 배열의 가로세로 사이즈, 즉 table board 사이즈랑 동일
private Point startIndex, endIndex; // 테이블 전체에서 하나만 뽑았기에 빈 공간이 많아서 블록만을 다루기 위해서 블록의 시작점(좌측상단) 끝점(우측하단)을 가지고있음
private int width, height; // 바로 위의 시작 끝과 어찌보면 중복되는 정보 ? block 배열 자체가 아닌 1이 차있는 찐 블록이 있는 공간의 너비 높이
Block(int n){
this.size = n;
this.block = new int[size][size];
this.count = 0;
this.startIndex = new Point(0,0);
this.endIndex = new Point(size-1, size-1);
this.width = n;
this.height = n;
}
// 해당 조각의 시작점부터 이어진 점을 bfs로 탐색하여 하나의 조각 완성
public void init(int[][] table, boolean[][] visited, Point start){
Queue<Point> queue = new LinkedList<>();
Point current, next;
queue.add(start);
visited[start.x][start.y] = true;
while (!queue.isEmpty()){
current = queue.poll();
block[current.x][current.y] = 1;
count++;
for(int k=0; k<4; k++){
next = new Point(current.x+dx[k], current.y+dy[k]);
if(next.x >= 0 && next.x < size && next.y >= 0 && next.y < size && !visited[next.x][next.y] && table[next.x][next.y] == 1){
queue.add(next);
visited[next.x][next.y] = true;
}
}
}
// 배열 사이즈가 table 사이즈와 동일하기 때문에 진짜 블록이 위치하는 위치를 뽑아내기 위한 함수 호출
removeEmptyLine();
}
// 첫 행, 끝 행, 첫 열, 끝 열을 각각 확인하면서 만일 1이 존재하지 않으면 블록이 존재하는 찐 위치를 위한 변수를 조정해준다.
public void removeEmptyLine(){
boolean xStart, xEnd, yStart, yEnd;
xStart = true;
xEnd = true;
yStart = true;
yEnd = true;
for(int i=0; i<size; i++){
for(int j=0; j<size; j++){
if(block[i][j] != 0) xStart = false;
if(block[size-1-i][j] != 0) xEnd = false;
if(block[j][i] != 0) yStart = false;
if(block[j][size-1-i] != 0) yEnd = false;
}
if(xStart){
startIndex.plusX();
height--;
}
if(xEnd){
endIndex.minusX();
height--;
}
if(yStart){
startIndex.plusY();
width--;
}
if(yEnd){
endIndex.minusY();
width--;
}
if(!xStart && !xEnd && !yStart && yEnd) break;
}
}
// 말그대로 블록 회전 !
public void rotation(){
int[][] result = new int[block[0].length][block.length];
int temp;
for(int i=0; i<block.length; i++){
for(int j=0; j<block[0].length; j++){
result[j][size-1-i] = block[i][j];
}
}
block = result;
// 너비 높이도 스왑 !
temp = width;
width = height;
height = temp;
// 시작점 ( 좌측상단 ) 끝점 ( 우측하단 ) 도 바뀌므로 업데이트 !
Point newStart = new Point(startIndex.y, size-1-endIndex.x);
Point newEnd = new Point(endIndex.y, size-1- startIndex.x);
this.startIndex = newStart;
this.endIndex = newEnd;
}
}
// 블록이 들어갈 수 있는지 판단하는 함수
public static boolean isPossible(Block block, int[][] board){
boolean result;
// 네 방향에 대해서
for(int i=0; i<4; i++){
// 첫 상태는 로테이션 하지 않음 ~
if(i != 0) block.rotation();
// 블록을 옮기면서
for(int a=0; a<=board.length- block.height; a++){
for(int b=0; b<=board.length-block.width; b++){
result = true;
// 블록이 해당 위치에 들어갈 수 있는지 판단
for(int c=0; c<block.height; c++){
for(int d=0; d<block.width; d++){
// 블록과 게임보드의 원소가 같으면 안된다. ( 둘 다 1이면 들어갈 수 없고, 둘 다 0이면 채워지지 않음 )
if(board[a+c][b+d] == block.block[c+block.startIndex.x][d+block.startIndex.y]) {
result = false;
break;
}
// 위의 조건을 다 만족해서 들어갈 수 있을 때, 블록의 범위외에 인접한 빈 공간이 있는지 확인 !
// 블록의 경계를 기준으로 x축 최상단 최하단 y축 최좌측 최우측에 대해서 해당 공간이 비어있어서 board의 원소가 0이고, 인접한 0 위치가 0인지 확인 !
if(c==0 && a!=0) if(board[a+c][b+d] == 0 && board[a+c-1][b+d] == 0){
result = false;
break;
}
if(c==block.height-1 && a!=board.length- block.height) if (board[a+c][b+d] == 0 && board[a+c+1][b+d] == 0){
result = false;
break;
}
if(d==0 && b!=0) if (board[a+c][b+d] == 0 && board[a+c][b+d-1] == 0){
result = false;
break;
}
if(d==block.width-1 && b!= board.length- block.width) if (board[a+c][b+d] == 0 && board[a+c][b+d+1] == 0){
result = false;
break;
}
}
if(!result) break;
}
// 위의 조건을 모두 통과해서 블록이 들어갈 수 있으면, 넣어주고( 즉 들어갈 위치를 1로 업데이트 해주고 ) 들어갈 수 있음을 의미하는 true 반환
if(result){
for(int c=0; c<block.height; c++) {
for (int d = 0; d < block.width; d++) {
board[a+c][b+d] += block.block[c+block.startIndex.x][d+block.startIndex.y];
}
}
return true;
}
}
}
}
return false;
}
public int solution(int[][] game_board, int[][] table) {
int answer = 0;
ArrayList<Block> blocks = new ArrayList<>();
Block block;
boolean[][] visited = new boolean[table.length][table.length]; // bfs를 위한 visited
// 각 원소들을 탐색하면서 방문하지 않은 1을 만나면 bfs로 블록 한 조각을 만들어서 리스트에 넣어준다.
for(int i=0; i<table.length; i++){
for(int j=0; j<table.length; j++){
if(table[i][j] == 1 && !visited[i][j]){
block = new Block(table.length);
block.init(table, visited, new Point(i, j));
blocks.add(block);
}
}
}
// 각 블록들에 대해서 들어갈 수 있는지 탐색해서 들어갈 수 있으면 해당 블록이 구성된 조각의 수만큼 answer 증가
for (Block value : blocks) if (isPossible(value, game_board)) answer += value.count;
return answer;
}
}