[알고리즘 문제풀이] 백준 12865 평범한 배낭

초장에 퇴근하고 공부하는 습관을 들이고자, 11월 1일이라는 좋은 핑계도 있겠다 오늘부터 다시 알고리즘과 CS 공부를 시작했다 ! ( CS는 언제적부터 정리했는데 아직도 못 끝냈다.. 내가 게으른 탓이겠지.. 아이패드에 정리 끝내면 하나씩 포스팅 할 것이다 .. )

그래서 오늘 푼 문제는 DP Well-Known인 기본 배낭 문제를 풀어보았다 ! DP 오랜만에 풀어서 금방 풀 수 있으려나 했는데 깔꼼하게 잘 풀려서 다행이었다 😇

문제 링크는 요기 > 백준 12865 - 평범한 배낭

문제

이 문제는 아주 평범한 배낭에 관한 문제이다.

한 달 후면 국가의 부름을 받게 되는 준서는 여행을 가려고 한다. 세상과의 단절을 슬퍼하며 최대한 즐기기 위한 여행이기 때문에, 가지고 다닐 배낭 또한 최대한 가치 있게 싸려고 한다.

준서가 여행에 필요하다고 생각하는 N개의 물건이 있다. 각 물건은 무게 W와 가치 V를 가지는데, 해당 물건을 배낭에 넣어서 가면 준서가 V만큼 즐길 수 있다. 아직 행군을 해본 적이 없는 준서는 최대 K만큼의 무게만을 넣을 수 있는 배낭만 들고 다닐 수 있다. 준서가 최대한 즐거운 여행을 하기 위해 배낭에 넣을 수 있는 물건들의 가치의 최댓값을 알려주자.

입력

첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)가 주어진다.

입력으로 주어지는 모든 수는 정수이다.

출력

한 줄에 배낭에 넣을 수 있는 물건들의 가치합의 최댓값을 출력한다.

예제

입력

4 7
6 13
4 8
3 6
5 12

출력

14

풀이 방법

DP답게 문제를 작은 단위부터 생각하려고 해야한다.

그러므로 첫번째 물건인 무게 6, 가치 13인 물건만을 넣는다고 생각해본다. 또한 배낭에 넣을 수 있는 무게가 1인 경우부터 7인 경우까지 차례로 늘려가며 이전의 값을 이용한다.

이전의 값을 이용하기 때문에, 아무 물건도 넣지 않는 경우인 0행과 배낭에 넣을 수 있는 무게가 0인 경우의 0열을 초기화 해주어야 한다. 당연히 물건이 없으면 배낭에 넣을 수 있는 무게가 몇이든 넣을 수 있는 가치는 0이고, 당연히 배낭에 넣을 수 있는 무게가 0이라면 물건이 몇개든 넣을 수 있는 가치는 0이다. 그러므로 0행과 0열은 모두 0으로 초기화해주면 된다.

초기화를 했으면 위에 말했듯이 작은 문제부터 해결해나가는데, 이전의 값을 어떻게 사용하면 좋을지 점화식을 세워야 한다.

먼저 배낭에 넣을 수 있는 무게가 현재 넣으려는 물건의 무게보다 작다면 넣을 수 없다. 그러므로 그냥 이전까지 물건으로 구한 배낭에 넣을 수 있는 물건의 최대 가치가 현재에도 최대일 것이다. (1) 만약 배낭에 넣을 수 있는 무게가 현재 물건 이상이라면, 현재것을 넣지 않는 이전까지 넣을 수 있는 최대 가치와 현재 것을 넣고 이전 물건까지 계산했을 때, (넣을 수 있는 무게 - 현재 물건의 무게)만큼 넣을 수 있을 때 최대값 중에서 더 큰 값이 된다.

즉 현재 것을 넣지 않았을 때의 최대 가치와 현재 것을 넣고, 남은 공간에 최대 가치만큼 넣은 경우를 더한 값 중에서 더 큰 값을 선택하는 것이다. 이것이 이 문제 풀이의 전부가 아닐까..

위에서 설명한 이전에 구해둔 값을 이용해서 현재 값을 구하는 관계를 점화식으로 정리해보면 아래와 같다.

dp[row][col] =
if( col < w ) dp[row-1][col] (1)
else max(dp[row-1][col], dp[row-1][col-w]+v) (2)

이를 이용해서 위의 예제를 하나씩 구해가면 아래와 같이 표가 완성된다.

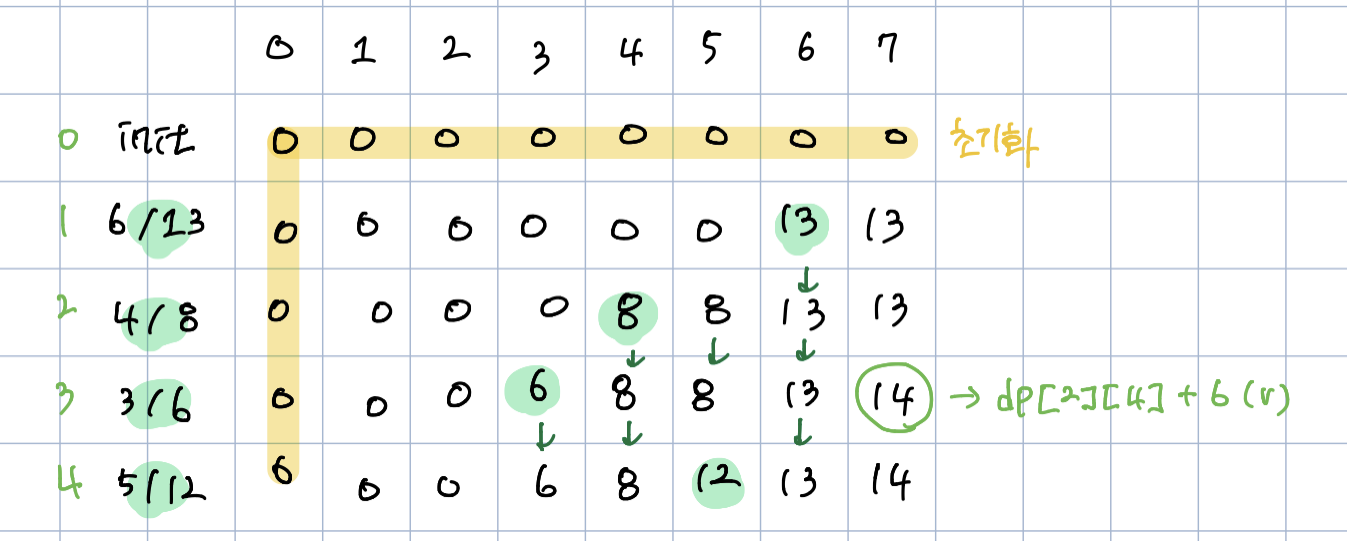
노란 부분은 처음 말했듯이 초기에 초기화해둔다. 민트, 초록, 연두 부분들을 보면 현재 것을 넣지 않았을 때의 최대값 즉 dp[row-1][col]과 현재 것을 넣고 남은 공간에 최대 가치를 넣은 경우 v+dp[row-1][col-w]중 더 큰 값을 채워넣는 것을 확인할 수 있다.

col-w가 의미하는 것은 현재것을 넣고 남은 공간을 의미한다. 그러므로 dp[row-1][col-w]는 현재 물건을 넣고 남은 공간에 넣을 수 있는 최대 가치가 되는 것이다. 더하여 dp[row-1][col-w]가 0인 경우도 있을 수 있고, 그 경우는 현재 물건만 넣는 경우가 되는 것이다.

설명이 너무 난리 법석이군,, gif로 보여주고 싶지만,, 시간이 늦었으니,, 줄인다,, 나만 이해했으면 됐어,, 특히 이건 웰논이라 설명도 많은 글이니

코드

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int n = Integer.parseInt(st.nextToken());
        int k = Integer.parseInt(st.nextToken());
        int[][] dp = new int[n+1][k+1];
        int w, v;
        for(int i=1; i<=n; i++){
            st = new StringTokenizer(br.readLine());
            w = Integer.parseInt(st.nextToken());
            v = Integer.parseInt(st.nextToken());
            for(int j=1; j<=k; j++){
                if(w > j) dp[i][j] = dp[i-1][j];
                else dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-w]+v);
            }
        }
        bw.write(dp[n][k] + "\n");
        bw.flush();
        bw.close();
        br.close();
    }
}