[알고리즘 문제풀이] 프로그래머스 순위

취준이 끝날 때까지는 알고리즘은 꾸준히 풀어보겠다는 마음을 다시 먹으며..! 시험 기간이지만 오랜만에 한 문제 풀어보았다 ! 화이팅 !

오늘 푼 문제는 프로그래머스 고득점 kit 그래프 분류에 있는 Level3 문제이다.
https://programmers.co.kr/learn/courses/30/lessons/49191

문제 설명

n명의 권투선수가 권투 대회에 참여했고 각각 1번부터 n번까지 번호를 받았습니다. 권투 경기는 1대1 방식으로 진행이 되고, 만약 A 선수가 B 선수보다 실력이 좋다면 A 선수는 B 선수를 항상 이깁니다. 심판은 주어진 경기 결과를 가지고 선수들의 순위를 매기려 합니다. 하지만 몇몇 경기 결과를 분실하여 정확하게 순위를 매길 수 없습니다.

선수의 수 n, 경기 결과를 담은 2차원 배열 results가 매개변수로 주어질 때 정확하게 순위를 매길 수 있는 선수의 수를 return 하도록 solution 함수를 작성해주세요.

제한사항

• 선수의 수는 1명 이상 100명 이하입니다.
• 경기 결과는 1개 이상 4,500개 이하입니다.
• results 배열 각 행 [A, B]는 A 선수가 B 선수를 이겼다는 의미입니다.
• 모든 경기 결과에는 모순이 없습니다.

입출력 예

n	results	return
5	[[4, 3], [4, 2], [3, 2], [1, 2], [2, 5]]	2

풀이 방법

이 문제는 승자와 패자가 정해져 있으므로, 1-n까지의 사람이 노드가 되고, 방향성이 있는 그래프라고 생각할 수 있다. 나는 승자 -> 패자, 즉 [4, 3]이 4 -> 3으로 매핑되는 그래프라고 생각하고 문제를 풀어 나갔다. 입출력 예를 그래프로 나타내면 아래와 같다.

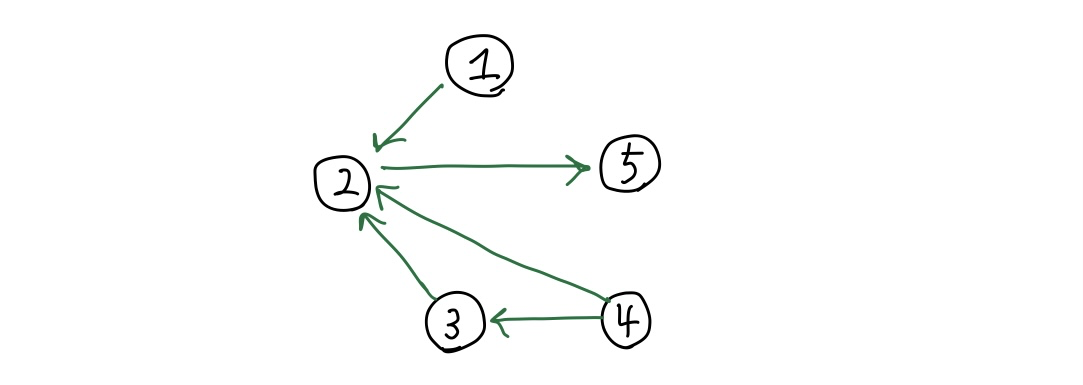
이 때, 한 사람이 이기는 사람과 지는 사람을 모두 파악해야 순위를 판단할 수 있으므로, 화살표가 나가는 방향 뿐 아니라 들어오는 방향까지 인식할 수 있도록 index에 대해서 들어오는 노드 리스트, 나가는 노드 리스트를 가지도록 아래와 같은 구조로 그래프를 구성하였다. ( 코드를 보면 명확히 이해할 수 있을 것이다. )

index : int	List < int >	List < int >

그리고 1번 노드부터 BFS를 이용해 직접 들어오거나 나가지 않더라도 depth를 거쳐서 들어오거나 나오는 노드까지 count하여 이기는 사람과 지는 사람의 수를 카운트한 후 그 수의 합이 n-1이라면 본인과 나머지 모든 노드간의 관계가 맺어진 것이므로 순위를 알 수 있다는 것을 이용하여 문제를 해결하였다.

위의 그래프에서 4가 이기는 사람은 2와 3이다. 또한 2가 이기는 5 역시도 4가 이길 수 있다. 3이 이길 수 있는 2는 이미 4가 이긴다는 것을 확인한 것이다. 5가 이길 수 있는 사람은 더 없으므로 4는 2, 3, 5의 세 명을 이길 수 있다. 나가고 들어오는 정보를 각 노드가 모두 가지고 있으므로 지는 것 역시 같은 원리로 구할 수 있는 것이다.

코드

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;

public class Solution {
    private static final int in = 0;
    private static final int out = 1;

    public static class Node{
        private ArrayList<ArrayList<Integer>> list;
        Node(){
            this.list = new ArrayList<>();
            for(int i=0; i<2; i++){
                list.add(new ArrayList<>());
            }
        }
    }

    public static int countNode(int node, ArrayList<Node> graph, boolean[] visited, int inOrOut){
        int count = 0;
        Queue<Integer> queue = new LinkedList<>();
        queue.add(node);
        while(!queue.isEmpty()){
            int current = queue.poll();
            visited[current] = true;
            for(int i=0; i<graph.get(current).list.get(inOrOut).size(); i++){
                if(!visited[graph.get(current).list.get(inOrOut).get(i)]){
                    queue.add(graph.get(current).list.get(inOrOut).get(i));
                }
            }
        }
        for(int i=1; i< visited.length; i++){
            if(visited[i]){
                visited[i] = false;
                count++;
            }
        }
        return count-1;
    }

    public static int solution(int n, int[][] results) {
        int answer = 0;
        ArrayList<Node> graph = new ArrayList<>();
        boolean[] visited = new boolean[n+1];
        for(int i=0; i<=n; i++){
            graph.add(new Node());
            visited[i] = false;
        }
        for(int[] result : results){
            graph.get(result[0]).list.get(out).add(result[1]);
            graph.get(result[1]).list.get(in).add(result[0]);
        }
        int inNode, outNode;
        for(int i=1; i<=n; i++){
            inNode = countNode(i, graph, visited, in);
            outNode = countNode(i, graph, visited, out);
            if(inNode + outNode == n-1) answer++;
        }
        return answer;
    }
}