문자열 검색 KMP 알고리즘

Jongmyung Choi·2023년 10월 26일

KMP algorithm

개요

기본기를 다지고자 JAVA EE랑 Spring 만을 사용해서 DB 없이 게시판을 구축 해봤는데 그 과정에서 게시글 검색에 적용한 KMP 알고리즘에 대해 정리하고자 글을 작성하였다.

Brute Force 검색

KMP 알고리즘에 대해 알아보기 전에 단순 비교하여 문자열을 검색했을 때의 시간복잡도를 한번 알아보자.
예를 들어 ABCABCABCD 에서 BCD를 찾는다고 가정해보자.

하나하나 일일이 비교하여 같으면 다음문자 비교를 하고 다르면 건너뛰고 .. 이렇게 반복한다.

이렇게 했을때 시간복잡도는 전체 문자열의 길이가 N 이고 찾으려는 문자열의 길이가 M 일때 O(NM) 이 된다.

KMP 알고리즘

KMP(Knuth-Morris-Pratt) 알고리즘은 접두사와 접미사를 이용하여 빠르게 매칭되는 문자열을 찾는 알고리즘이다.

KMP 알고리즘의 핵심은 접두사와 접미사를 이용하여 불일치가 발생하기 전 부분은 다시 비교하지 않고 건너뛰어서 검색을 한다는 것이다.
이론상 가장 빠른 알고리즘이며 무려 시간복잡도가 O(N+M)이라고 한다.
조금 자세히 살펴보자.

접두사와 접미사

접두사와 접미사 뭔가 오랜만에 듣는 단어다..
말 그대로 접두사는 머리에 있는거고 접미사는 꼬리에 있는거다.
예를 들어보자면

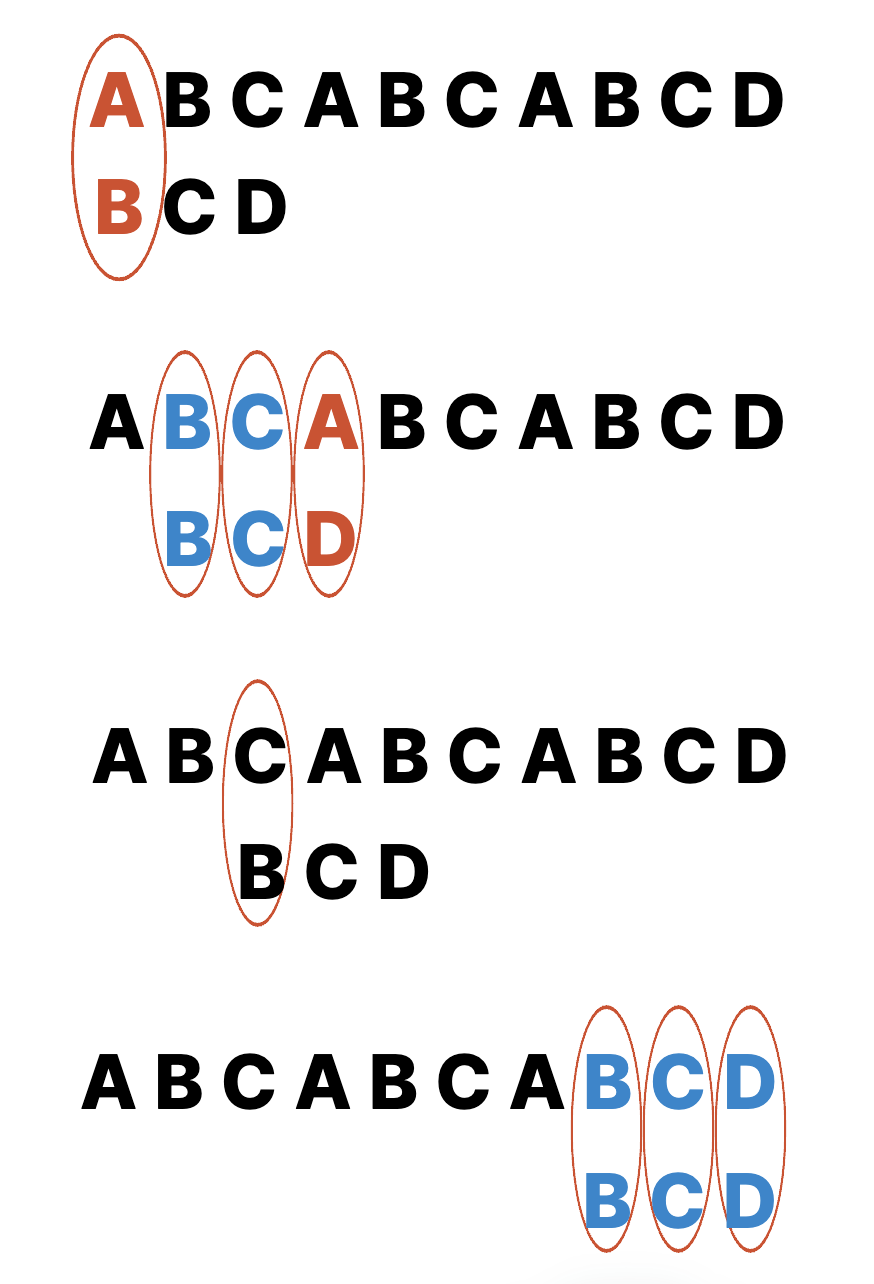
빨간색 영역은 접두사고 파란색 영역은 접미사 이다.
(하지만 접두사와 접미사는 전체 길이가 될수는 없다. ABCABCABCD )
그러면 이 접두사와 접미사를 어떻게 알고리즘에 적용한다는 것일까?
KMP 알고리즘에서 주목한건 접두사와 접미사가 일치하는 최대 길이 이다.

접두사와 접미사가 일치하는 최대 길이

ABACAABA 에서 접두사와 접미사가 일치하는 최대 길이를 알아보자

길이	문자열	접두사	접미사	최대 일치 길이
1	A			0
2	AB	A	B	0
3	ABA	A	A	1
4	ABAC	A	C	0
5	ABACA	A	A	1
6	ABACAA	A	A	1
7	ABACAAB	AB	AB	2
7	ABACAABA	ABA	ABA	3

이런식으로 최대 길이가 만들어질 것이다.
이 최대 일치 길이를 저장해두는 배열이 필요한데 이것을 구하는 자바 코드이다.

int[] makeTable(String pattern) {
	int n = pattern.length();
	int[] table = new int[n];
		
	int idx=0;
	for(int i=1; i<n; i++) {
        // 일치하는 문자가 발생했을 때 계속 진행하고 연속적으로 더 일치하지 않으면 idx = table[idx-1]로 돌려준다.
		while(idx>0 && pattern.charAt(i) != pattern.charAt(idx)) {
			idx = table[idx-1];
		}
			
		if(pattern.charAt(i) == pattern.charAt(idx)) {
			table[i] = ++idx;  
		}
	}
	return table;
}

이 과정을 거치면 table 배열에는 0,0,1,0,1,1,2,3 이 들어가게 된다.
이렇게 최대 일치 길이를 저장해두는 배열을 가지고 이제 효율적으로 검색을 할수 있다.

알고리즘 적용

이제 이 배열을 어떻게 사용할지에 대해 알아보자.
우리는 전체 문자열이 ababacabacaabacaaba 인 곳에서 abacaaba를 찾아볼 것이다.

먼저 하나하나 앞에서 부터 비교한다.
전체 문자열의 인덱스 = i , 내가 찾고자하는 문자열의 인덱스 =j 라고 하고
i를 증가시키면서 j와 비교한다.

i=0 j=0

i=1 j=1

i=2 j=2

i=3 j=3

진행하다가 이렇게 일치하지 않는 문자가 나왔을 때 j=2 일때까지 일치했으니까 최대 일치길이 table[2] = 1 로 j는 되돌아가고 i는 그대로 있는다.

i=3 j=1

i=4 j=2

i=6 j=7

이렇게 계속 반복하여 정답을 찾아낸다.

이 방법을 사용하면 O(N + M)의 시간복잡도가 사용된다.
이는 문자열을 한번만 읽고 탐색하는 것과 같은 시간 복잡도 이므로 이론상으로 가장 빠른 문자열 탐색 알고리즘이다.

코드

private static void KMP() {
		int j = 0;
		for (int i = 0; i < origin.length(); i++) {
			// 맞는 위치가 나올 때까지 j - 1칸의 공통 부분 위치로 이동
			while(j > 0 && origin.charAt(i) != pattern.charAt(j)) {
				j = pi[j - 1];
			}
			// 맞는 경우
			if(origin.charAt(i) == pattern.charAt(j)) {
				if(j == pattern.length() - 1) {
					result = 1;
					break;
				}
				//맞았지만 패턴이 끝나지 않았다면 j를 하나 증가
				else
					++j;
			}
		}
		System.out.println(result);
	}