이번 포스팅은 standford university의 cs231 lecture 6을 공부하고, 강의와 슬라이드를 바탕으로 정리한 글임을 밝힙니다.

Reference

💻 유튜브 강의: Lecture 6 | Training Neural Networks I
💻 한글 강의: cs231n 5강 Training NN part 1
📑 slide: PDF
📔 How To Make Deep Learning Models That Don’t Suck
📔 Learning Process of a Deep Neural Network
📔 How to Initialize Weights in Neural Networks?

Contents

• Activation Functions
• Data Preprocessing
• Weight Initialization
• Batch Normalization
• Babysitting the Learning Process
• Hyperparameter Optimization

Activation Functions

Activation Function이란 무엇입니까?

Activation Function은 neuron에서 제공되는 최종 값을 제공합니다.

기본적으로 input을 특정 범위의 출력으로 변환하는 단순한 함수입니다. 이 작업을 다른 방식으로 수행하는 다양한 유형의 Activation Function이 있습니다.

network가 data의 복잡한 패턴을 학습할 수 있도록 이 기능을 추가하였습니다.

$x$는 입력, $w$ 가중치로 정의되며 network의 출력으로 전달되는 값인 $f(x)$를 전달. 이것은 최종 출력이 되거나 다른 layer의 입력이 됩니다.

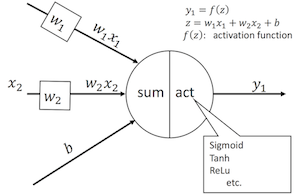
또한, Activation Function은 neruon의 output에게 non-linearity을 도입합니다.

activation function은 미분할 수 있어야 하며, 그렇지 않으면 가중치 업데이트(backpropagation)이 실패한다는 개념이 딥러닝의 핵심 아이디어라고 할 수 있습니다.

그렇다면 왜 non-linearity(비선형)이 필요할까요?

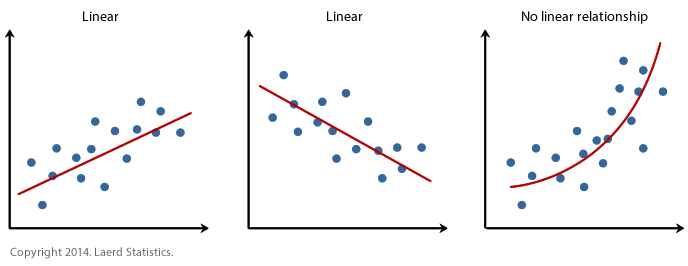
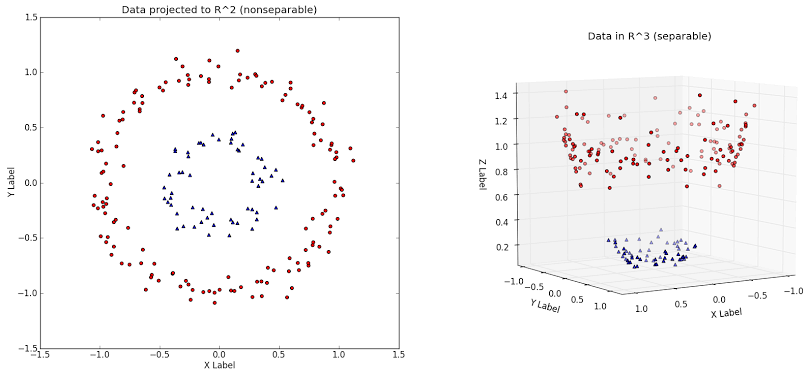
non-linearity는 output이 input의 변화에 따라 변하지 않는다고 생각할 수 있습니다.

위의 그림과 같이 circle 또는 elliptical 같은 non-linearity data가 있다고 가정하고, data point가 positive class or nagative class에 속하는지 분류하는 작업입니다.

이러한 경우엔 linearity model을 사용할 수 없습니다.

activation function은 input에 대한 non-linear transformation을 수행하여 더 복잡한 작업을 학습하고 수행할 수 있도록 합니다.

Sigmoid

sigmoid function은 아래와 같습니다.

그래프로 나타내면 이렇습니다.

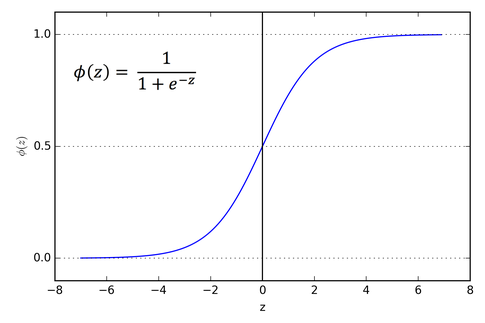
그래프를 보면 y의 값의 범위가 [0, 1] 임을 알 수 있습니다.

*0과 1 사이의 값으로 나온다고 하여 Squash한다고 표현하고, squash function이라고도 부릅니다.

sigmoid function 같은 경우는 90년대 가장 인기 있는 activation function이었으나 현재는 잘 사용하지 않습니다.

그 이유는 무엇일까요? 하나씩 살펴보겠습니다.

1) Vanishing Gradient

• Saturated neurons 'kill' the gradients

첫 번째는 Vanishing Gradient 문제입니다.

앞서 범위가 [0, 1]라고 보았는데요. 0의 가까운 값에서만 simgoid가 active된다고 볼 수 있습니다.

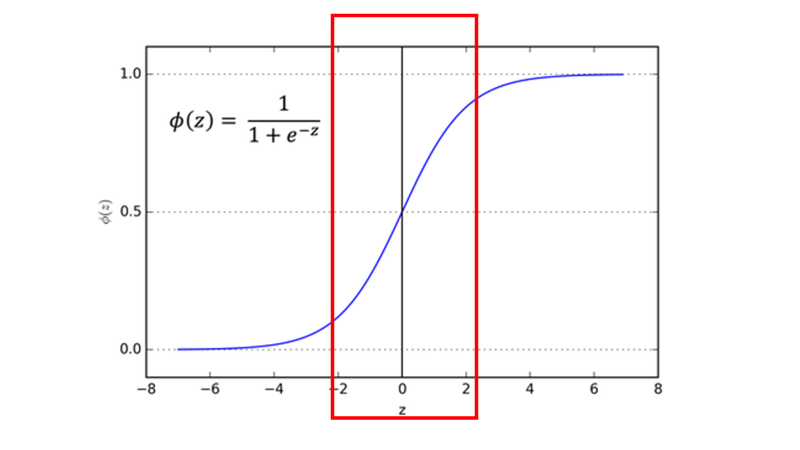
그래프의 가운데 지점(빨간색 박스)을 active region of simgoid 이라고 합니다.

만약 $W$가 10이거나 -10인 경우(매우 작거나, 매우 클 때)에는 1 또는 0의 값으로 수렴하게 됩니다.

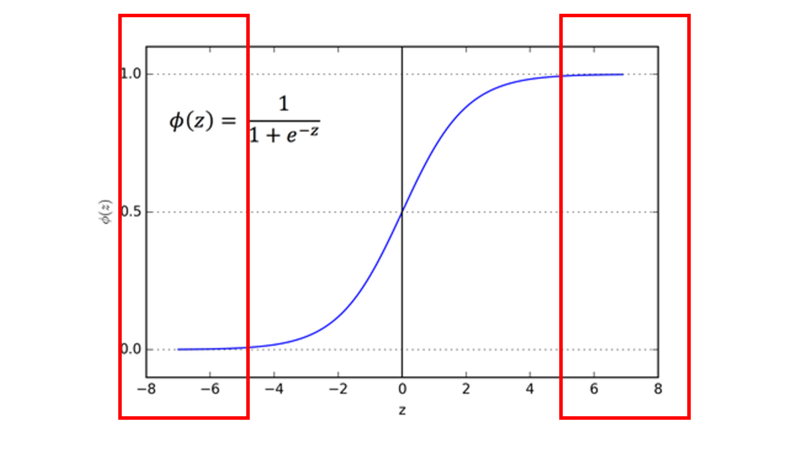
그래프의 양쪽 끝 지점을 saturated region이라고 합니다.

정리하자면,

x의 값이 꽤 작거나 꽤 큰 경우에는 local gradient 값이 0이 되어 gradient가 없어지는 즉, backpropagation이 stop 되는 결과가 나타나게 됩니다.

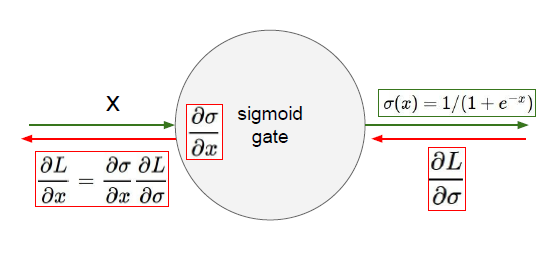
2) Not zero-centered

• Sigmoid outputs are not zero-centered

sigmoid의 결과는 0 중심이 아닙니다. 모든 값은 0 이상의 값을 가져서 slow convergence를 가져옵니다.

$x$가 항상 양수일 때,

3) Compute expensive

• $exp()$ is a bit compute expensive

보통 지수 함수 $exp()$의 경우 연산이 굉장히 커서, 성능이 저하 된다고 볼 수 있습니다.

tan h(hyperbolic tangent)

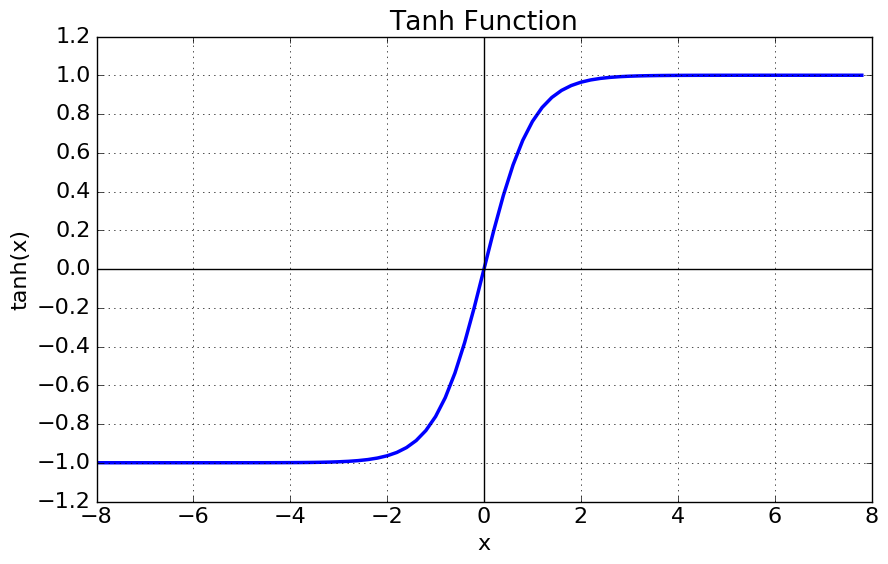
$tanh$의 경우 data가 0을 중심으로 합니다. 이는 입력 데이터의 평균이 0 근처에 있음을 의미하고, sigmoid 보다 성능이 더 좋은 주된 이유가 됩니다.

• $tanh$는 [-1, 1]의 값을 갖습니다.
• zero centered 입니다.
• saturated 될 때 gradient는 여전히 죽습니다.

$tanh$가 $sigmoid$ 보다 성능이 더 좋은 이유는 무엇이고, convergence가 더 빠른 이유는 무엇일까요?

$tanh$와 $sigmoid$는 둘 다 +inf, -inf에 접근할 때 일부 유한 값에 점근하는 monotonically increasing function(단조 증가 함수)입니다.

또한, 둘 다 $S$자형 곡선을 가진 함수입니다.

눈으로 비교해 보았을 때 유일한 차이점은 sigmoid가 0과 1 사이에 있고, tanh는 1과 -1 차이에 있다는 점입니다.

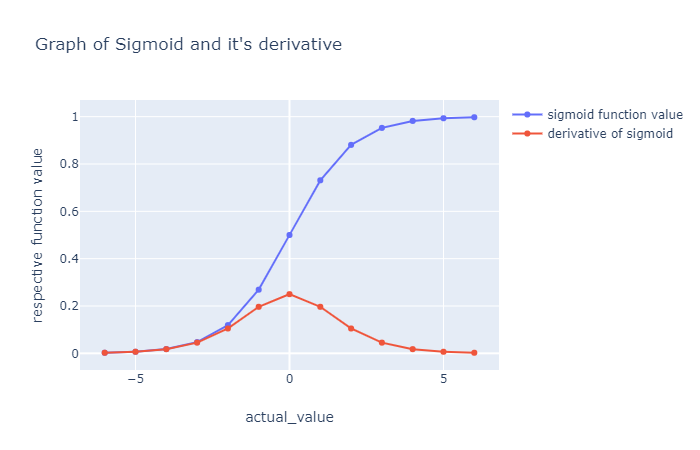
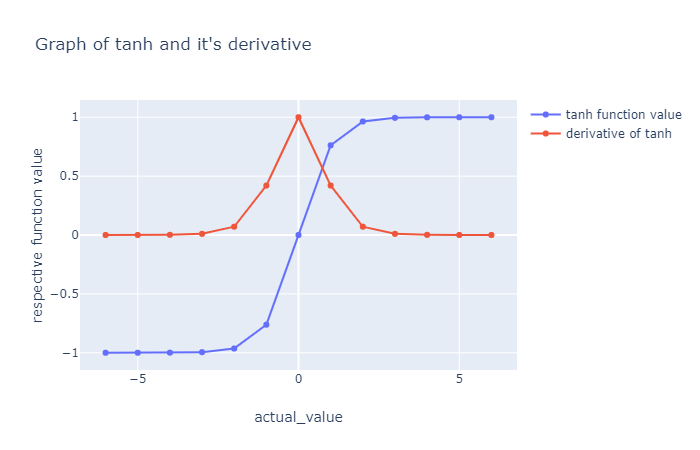
*위 그래프의 파란선은 기본 function이며, 빨간선은 함수를 미분한 경우입니다.

입력값에 따라 평균값이 달라질텐데, $tanh$는 $sigmoid$와 달리 항상 0에 가까울 것입니다.

$tanh$는 입력이 nomarlize되고 output을 생성할 가능성이 더 높습니다. 그 이유는 원점에 대한 대칭이기 때문에 평균이 0에 가까워지는 것입니다.

• zero centered라는 것은 data가 0을 중심으로 한다는 것이고, input data의 mean이 0 근처에 있다는 뜻입니다!

ReLU(Rectified Linear Unit)

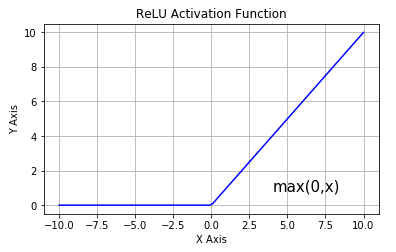
ReLU 함수는 단조 도함수입니다. 이 함수는 음수 입력을 받으면 0을 반환하지만, 양수 값 x에 대해 해당 값을 다시 반환합니다.

따라서 0에서 무한대의 범위를 갖는 출력을 제공합니다.

강의에서 언급된 ReLU의 특징입니다.

• Computes $f(x) = max(0,x)$
• Does not saturate (in+region)
• Very computationally efficient
• Converges much faster than sigmoid/tanh in practice (e.g 6x)
• Not zero-centered output
• An annoyance

hint: what is the gradient when x < 0 ?

• active ReLU
• dead ReLU will never activate → never update

people like to initialize ReLU neurons with slightly positive biases (e.g 0.01)

강의에서도 핵심만 짚고 넘어갔습니다.

Introduction to ReLU Activation Function

$ReLU$는 하도 많이 들어서 이름 자체는 익숙한 activation function이라 생각하는데요. 심지어 function 자체도 굉장히 simple해서 쉽게 다가옵니다.

저는 $ReLU$를 공부할 때, 두 가지 관점으로 접근하면 좋다고 합니다. 둘 다 결국 일맥상통하는 이야기이긴 합니다.

첫 번째로

왜 $ReLU$는 $sigmod$와 $tanh$보다 더 좋은 convergence를 보여주는가?

두 번째로

왜 $ReLU$가 가장 좋은 $activation$ $functuon$인가?

입니다.

덧붙여서

변형된 $ReLU$ 함수가 나오게 된 배경은 무엇인가?

정도로 살펴보려고 합니다.

Better Convergence

Sigmoid

sigmoid 함수의 값이 너무 작거나 크면 도함수($\sigma'(x)$)는 0에 가까워지며 작아집니다.

error가 sigmoid activated neural networks에서 back propagation하는 동안, 기울기 저하가 발생하고, gradient가 사라지게 됩니다.

초기 레이어에 대한 gradient 값이 줄어들고 해당 레이어는 제대로 학습할 수 없습니다. 즉, 네트워크의 깊이와 값이 0으로 이동하는 활성화로 인해 기울기가 사라지는 경향이 있습니다.

Problem

• Gradient Degradation
• Vanishing Gradient

ReLU

error가 relu activated neural networks에서 back propagation하는 동안, gradient는 기울기 저하가 발생하지 않습니다.

반면 ReLU는 입력이 커질 때 기울기가 안정되지 않거나 "포화"되지 않으므로 위의 문제에 직면하지 않습니다. 이러한 이유로 ReLU를 사용하는 모델은 더 빨리 수렴합니다.

The best activation function

위에서 보았듯이 ReLU 함수는 간단하고 복잡한 수학이 없기 때문에 무거운 계산으로 구성되어 있지 않습니다.

따라서 모델을 훈련하거나 실행하는 데 더 적은 시간이 소요됩니다.

ReLU 활성화 함수를 사용할 때의 이점을 고려하는 또 다른 중요한 속성은 sparsity(희소성)입니다.

일반적으로 대부분의 항목이 0인 행렬을 sparse matrix(희소 행렬)이라고 하며 마찬가지로 일부 가중치가 0인 신경망에서 이와 같은 속성을 원합니다.

sparsity은 종종 더 나은 predictive power와 overfitting/noise가 적은 간결한 모델을 생성합니다.

sparse network에서는 뉴런이 실제로 문제의 의미 있는 측면을 처리할 가능성이 더 큽니다.

예를 들어, 이미지에서 사람의 얼굴을 감지하는 모델에는 귀를 식별할 수 있는 뉴런이 있을 수 있으며, 이미지가 얼굴이 아니고 배나 산인 경우 활성화되지 않아야 합니다.

ReLU는 모든 음수 입력에 대해 출력 0을 제공하기 때문에 주어진 단위가 전혀 활성화되지 않아 네트워크가 sparse해질 가능성이 있습니다.

Exploding Gradient

ReLU 활성화 함수에는 exploding gradient과 같은 몇 가지 문제가 있습니다.

exploding gradient는 vanishing gradient의 반대 개념입니다.

큰 오류 gradient가 누적되어서 훈련 중에 신경망 모델 가중치가 매우 크게 업데이트되는 경우에 발생합니다.

이로 인해 모델이 불안정하고 훈련 데이터에서 학습할 수 없게 됩니다.

또한, 모든 음수 값에 대해 0이 되는 점이 단점이 되기도 합니다.

이 문제를 "dying ReLU"라고 합니다.

ReLU neuron이 음수 쪽에 붙어 있고 항상 0을 출력하면 "dying"했다고 봅니다.

음수 값에서 ReLU의 gradient 범위도 0입니다.

neuron이 음수가 되면 다시 살아날 가능성이 거의 없습니다.

이러한 뉴런은 input을 구별하는 데 아무런 역할도 하지 않으며 본질적으로 쓸모가 없습니다.

시간이 지나면서 network의 상당 부분이 아무것도 하지 않게 될 수도 있습니다.

dying하는 문제는 learning rate가 너무 높거나 negative bias가 클 때 발생하기 쉽습니다.

낮은 learning rate는 종종 이 문제를 완화하기도 합니다. (learning rate에 대한 내용은 더 뒤쪽에서 다뤄집니다.)

또는, 다음에 나오는 Leaky ReLU를 사용할 수 있습니다.

Leaky ReLU

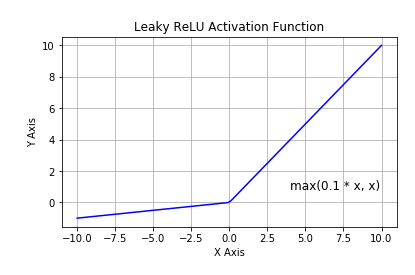
Leaky ReLU는 ReLU Function의 Dying 문제를 극복한 ReLU Activation Function의 확장입니다.

Dying ReLU 문제는 제공된 모든 입력에 대해 비활성화되어 Neural Network의 성능에 영향을 미칩니다.

이 문제를 해결하기 위해 ReLU Activation Function과 달리 Negative 입력에 대한 음의 기울기가 작게 조정된 Leaky ReLU가 있습니다.

$0.01$의 일정한 기울기를 갖습니다. Leaky ReLU의 한계는 복잡한 분류에 사용할 수 없는 선형 곡선을 가지고 있다는 것입니다.

강의에서 언급된 정리 내용

• Does not saturate
• Computationally efficient
• Converges much faster than sigmoid/tanh in practice! (e.g. 6x)
• will not ‘die’

PReLU(Parametric Recifier)

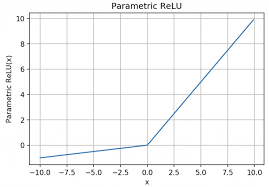
→ backprop inot $\alpha$ parameter

식을 나누면

Parametric Rectified Linear Unit 또는 PReLU는 음수 값에 대한 기울기로 기존의 rectified된 단위를 일반화하는 활성화 함수입니다.

만약 $\alpha$가 0이면 ReLU, 0.01이면 Leaky ReLU와 같아집니다.

PReLU는 어느 곳에 쓰일까요?

PReLU는 다른 parameter(e.g. Weight, bias)에 더 잘 적응할 수 있도록 훈련 중에 작은 값을 학습할 수 있도록 도와줍니다.

backprop을 사용할 때 기울기 매개변수를 학습할 수 있습니다.

ELU(Exponentaial Linear Units)

$f(x)= \begin{cases}x&if x>0\\ \alpha(exp(x)-1)&if x \le 0\end{cases}$

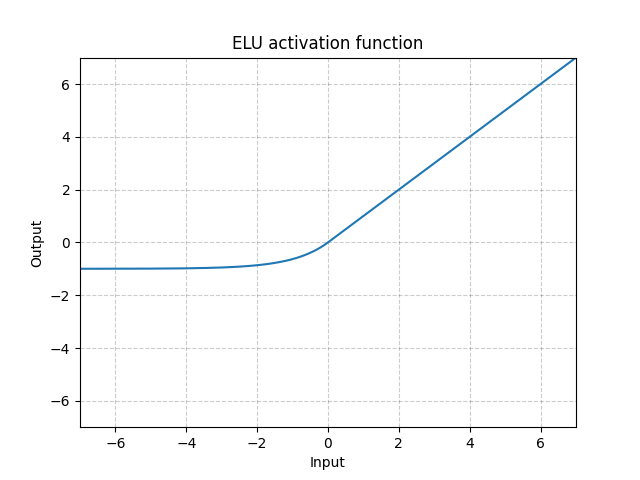
ELU는 Vanishing Gradient나 Exploading Gradient 문제를 겪지 않습니다.

ELU를 사용하면 훈련 시간이 줄어들고, 정확도가 높아집니다.

또한, 연속 함수여서 모든 지점에서 미분이 가능합니다.

ReLU와 달리 ELU는 음숫값을 가지므로 함수의 평균이 0으로 이동하고, 이 점에서 더 빠르게 convergence한다고 주장됩니다.

ELU 함수는 지수함수여서 계산 속도는 느리지만 더 빠른 convergence로 빠르게 학습되는 원리입니다.

장점

• 모든 점에서 연속적이며 미분 가능
• training time이 빠름
• dying ReLU의 문제가 없음(음수 값의 기울기가 0이 아니라서)
• non-saturating activation function이라서 exploding or vanishing gradients 문제를 겪지 않음
• ReLU, sigmoid, Hyperbolic Tangent보다 높은 accuracy

단점

• 계산 속도가 느림
• test 때, ELU는 느린 편

강의에서 정리된 내용

• All benefits of ReLU
• Does not die
• Closer to zero mean outputs
• Computation requires $exp()$

Maxout ‘neuron’

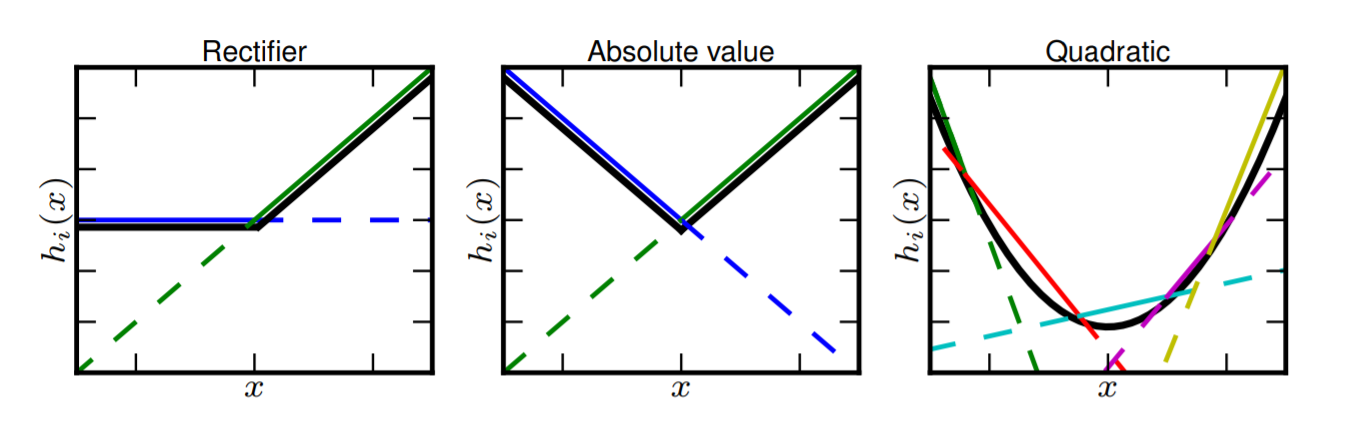
Maxout unit은 "n개의 linear functions"의 값 중 최대값을 취합니다.

linear function의 수는 미리 결정됩니다.

여러 선형 함수를 사용하여 함수를 근사하는 것을 piece-wise linear approximation(PWL) 라고 합니다.

강의에서 정리된 내용

• Does not have the basic form of dot product → nonlinearity
• Generalizes ReLU and Leaky ReLU
• Linear Regime! Deos not saturate! Does not die!
• problem: doubles the number of parameters/neurons

TLDR: In practice:

• Use ReLU. Be careful with your learning rates
• Try out Leacky ReLU / Maxout / ELU
• Try out tanh but don’t expect much
• Don’t use sigmoid

Their Derivatives

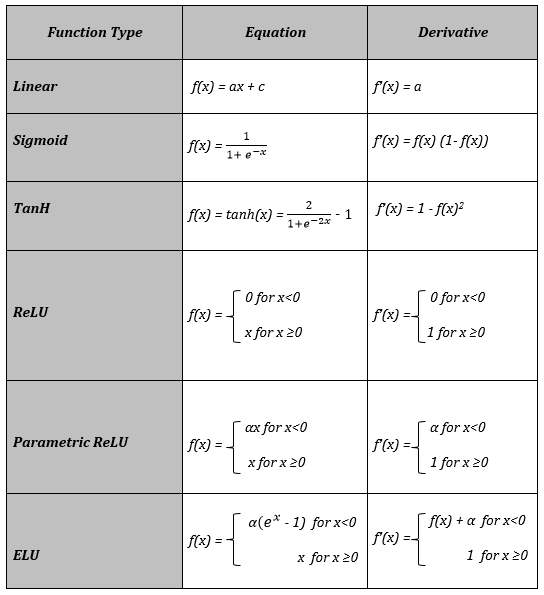
Data Preprocessing

Step 1: Preprocess the data

data matrix를 preprocessing하는데 세 가지의 일반적인 형식이 있습니다.

• X는 data, N은 데이터 수, D는 차원입니다.

1. Mean subtraction
2. Normalization
3. PCA and Whitening

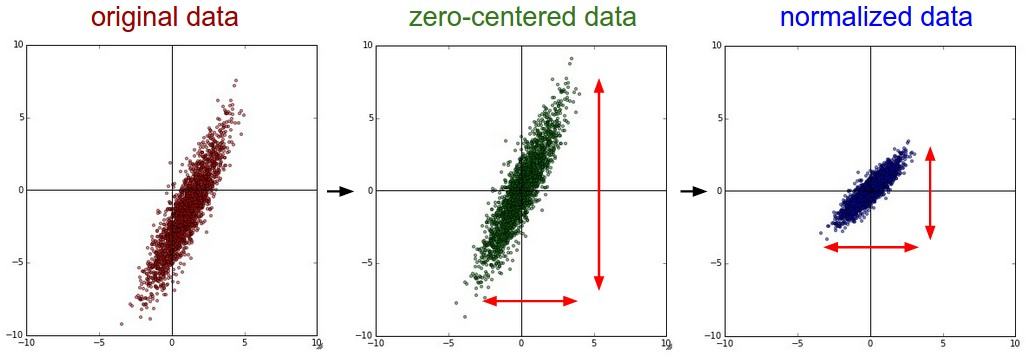
Mean subtraction

Mean subtraction은 가장 흔한 data preprocessing 방법 중 하나입니다.

data의 각각의 모든 feature에 평균을 빼주는 작업입니다.

이렇게 하면 모든 차원을 따라 원점을 중심으로 모이게 됩니다. (zero-centered data)

• X -= np.mean(X, axis = 0)

특히 이미지의 경우 편의를 위해 모든 픽셀에서 단일 값을빼거나

X -= np.mean(X)이거나 RGB 3 channel에서 별도로 빼는 것이 일반적일 수 있습니다.

Normalization

Normalization은 data의 차원이 동일한 척도가 되도록 정규화하는 것을 의미합니다.

각 차원이 zero-centered되면 표준편차로 각 값을 나누는 방법입니다.

• X /= np.std(X, axis=0)(normalized data)

이미지의 데이터의 경우, zero-centered 는 해주고 일반적으로 normalized는 해주지 않습니다.

그 이유로 목적 자체가 특정 범위에 들어가도록 하는 것인데, 이미지의 경우 pixel 값이 0~255 사이에 들어가 있으므로 추가 전처리 단계를 수행하는 것이 의미없습니다.

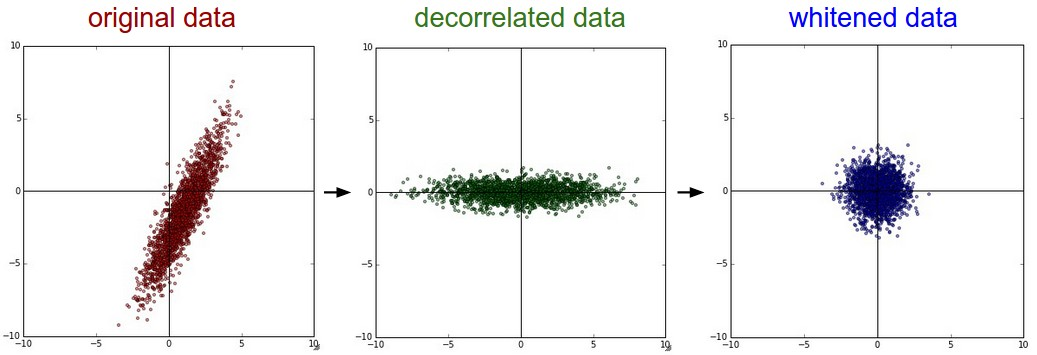
PCA and Whitening

preprocessing의 또 다른 형태입니다. 위의 과정에 따라 data가 중앙에 배치되고, 데이터의 correlation를 알 수 있는 covariance matrix을 계산합니다.

# Assume input data matrix X of size [N x D]
X -= np.mean(X, axis = 0) # zero-center the data (important)
cov = np.dot(X.T, X) / X.shape[0] # get the data covariance matrix

데이터 공분산 행렬의 (i,j) 요소는 데이터의 i번째 차원과 j번째 차원 간의 covariance을 포함합니다.

특히 이 행렬의 대각선에는 분산이 포함됩니다.

또한, covariance matrix은 대칭입니다. 데이터 covariance matrix의 SVD 분해를 계산할 수 있습니다.

U,S,V = np.linalg.svd(cov)

여기서 U는 eigenvectors이며 S는 single value의 1차원 배열입니다.

data의 상관관계를 없애기 위해 원본(그러나 0 중심) 데이터의 eigenbasis에 사영합니다.

Xrot = np.dot(X, U) # decorrelate the data

Xrot_reduced = np.dot(X, U[:,:100]) # Xrot_reduced becomes [N x 100]

Whitening은 eigenbasis의 data를 가져오고 모든 차원을 eigenvalue로 나누어 scale을 정규화합니다.

이 변환은 input data가 multivariable gaussian일 경우, whitening된 data가 zero mean과 identity covariance matrix이 동일한 가우스가 됩니다.

아래와 같은 형식을 취합니다.

# whiten the data:
# divide by the eigenvalues (which are square roots of the singular values)
Xwhite = Xrot / np.sqrt(S + 1e-5)

강의 내용 정리

In practice, you may also see PCA and Whitening of the data

• PCA
  • data has diagonal covariance matrix
• Whitening
  • Covariance matrix is the identify matrix

→ 이미지의 경우에는 잘 하지 않음

e.g. consider CIFAR-10 example with [32,32,3] images

• Subtract the mean image (e.g. AlexNet)
  (mean image = [32,32,3] array)
• Subtract per-channel mean (e.g. VGGNet)
  (mean along each channel = 3 numbers)

Weight Initialization

neural network에서 weight initialization 기법의 중요성과 잘못된 가중치 초기화로 인해 발생하는 문제를 다뤄보겠습니다.

linear 및 logistic regression 같은 regression 기술에서 가중치를 0 또는 임의의 값으로 초기화하지만 동일한 기술은 neural network에 적합하지 않은 것으로 판명났습니다.

Zero initialization

모든 가중치를 0으로 초기화하면 뉴런이 훈련 중에 동일한 feature를 학습하게 됩니다. backpropagation도 동일한 연산이 진행될 것입니다.

사실 일정한 초기화 방식은 성능이 매우 좋지 않습니다.

두 개의 hidden units이 있는 신경망을 고려하고 모든 bias를 0으로 초기화하고 weight을 일정한 α로 초기화한다고 가정합니다.

이 network에서 input ($x_1, x_2$)을 전달하면 두 hidden units의 출력은 relu ($αx_1 + αx_2$)가 됩니다.

따라서 두 hidden units은 cost에 동일한 영향을 미치므로 동일한 기울기가 발생합니다.

따라서 두 뉴런은 훈련 전반에 걸쳐 대칭적으로 진화하여 서로 다른 뉴런이 서로 다른 것을 학습하는 것을 막습니다.

Random Initialization

가중치에 임의의 값을 할당하는 것이 0을 할당하는 것보다 낫습니다.

하지만 가중치가 아주 크거나 작은 값으로 초기화되면 두 가지 문제에 직면하게 됩니다.

i) Vanishing Gradient

가중치가 단위 행렬보다 약간 작게 초기화되는 경우를 가정해보겠습니다.

이것은 $y = W[L]0.5^{L-1}x$로 단순화 되고 활성화 $\alpha [l]$ 값은 $l$에 따라 기하급수적으로 감소합니다.

이런 activations가 backward propagation에서는 vanishing gradient 문제에 직면합니다.

parameter에 대한 cost의 gradient가 너무 작아서 최솟값에 도달하기 전 cost가 convergence하게 됩니다.

ii) Exploading Gradient

가중치가 매우 높은 값으로 초기화되면 exploding gradient 문제에 직면합니다.

모든 가중치가 단위 행렬보다 약간 높게 초기화되는 경우를 가정해보겠습니다.

이건 $y = W[L]1.5^{L-1}x$로 단순화 되고 활성화 $\alpha [l]$ 값은 $l$에 따라 기하급수적으로 증가하게 됩니다.

똑같이 backpropagation에 사용되면 exploding gradient 문제가 발생합니다!

즉, parameter에 대한 cost의 gradient가 너무 크면, cost가 최솟값을 중심으로 진동하게 됩니다.

결국 overshooting이 발생되어 모든 neuron이 saturated 됩니다

New initialization technique

network의 activation이 Vanishing Gradient와 Exploading Gradient 되는 것을 방지하기 위해 다음과 같은 규칙을 따릅니다.

1. activations의 평균은 0이 되어야 한다.
2. activation의 분산은 모든 layer에서 동일하게 유지되어야 한다.

이런 사항에 따라 2015년 He et al. (2015)는 이 문제를 해결할 수 있는 activation aware initialization of weights를 제안했습니다.

이는 ReLU를 위한 가중치 초기화 문제였으며, ReLU 및 Leaky ReLU 또한 그라디언트 소실 문제를 해결했습니다.

He Normal initialization

신경망 ReLU가 활성화되면 He 초기화는 해당 출력의 분산을 대략 1로 만들기 위해 선택할 수 있는 방법 중 하나입니다.

$W$~$N(0,σ)$

Random initialization에 위에 주어진 값을 곱하기만 하면 됩니다.

Xavier Normal initialization

신경망이 $tanh$ 또는 $sigmoid$를 활성화하면 가중치 초기화를 위해 Xavier Normal 방법을 선택할 수 있습니다.

$W$ ~ $N(0,σ)$

Random initialization에 위에 주어진 값을 곱하기만 하면 됩니다.

이 방법은 초기화를 위한 좋은 시작점 역할을 하며 exploding and vanishing gradient 문제를 완화합니다.

너무 크지도 작지도 않은 가중치를 설정하여, 느린 convergence를 피하고 최솟값에서 계속 진동하지 않도록 합니다.

Key Points

• 가중치 값은 작아야 합니다.
• 가중치는 모든 반복 또는 epoch에 대해 동일하지 않아야 합니다.
• 가중치는 분산이 좋아야 합니다.

Batch Normalization

수십 개의 layer가 있는 DNN을 훈련하는 것은 학습 알고리즘의 초기 무작위 가중치와 구성들에 민감할 수 있습니다.

그 이유는 가중치가 업데이트 될 때, 각 mini-batch 이후에 네트워크의 깊은 layer에 대한 입력 분포가 변할 수 있기 때문인데요. 이런 변화를 “internal covariate shift”이라고도 합니다.

배치 정규화는 각 미니 배치에 대한 계층에 대한 입력을 표준화하는 매우 깊은 신경망을 훈련하는 기술입니다.

이는 training process를 안정화하고 DNN을 훈련하는 데 필요한 train epoch 수를 획기적으로 줄이는 효과가 있습니다.

또한 Vanishing Gradient 문제가 발생하지 않도록 2가지 단계를 취하는데요.

1. Normalize:

$\hat{x} ^{(k)} = \frac {x^{(k)}-E[x^{(k)}]}{\sqrt{Var[x^{(k)}]}}$

2. 정규화 조정

$y^{(k)} = \gamma ^{(k)} \hat{x} ^{(k)} + \beta ^{(k)}$

• $\gamma$: normalize한 값들을 scaling
• $\beta$: shift 함

Note, the network can learn:

to recover the identity mapping.

1. Compute the empirical mean and variance independently for each dimension
2. Normalize

보통 FC layer 뒤, nonlinearity 앞에 옵니다.

Babysitting the Learning Process

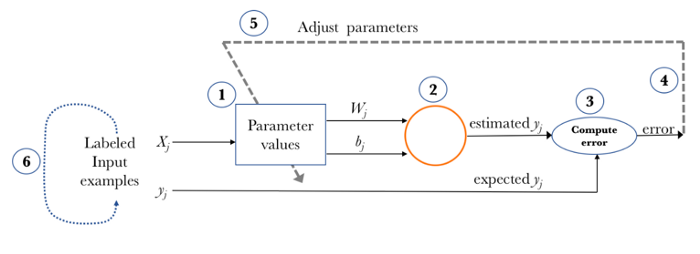
Learning Process를 다시 천천히 살펴보겠습니다.

신경망 훈련 단계

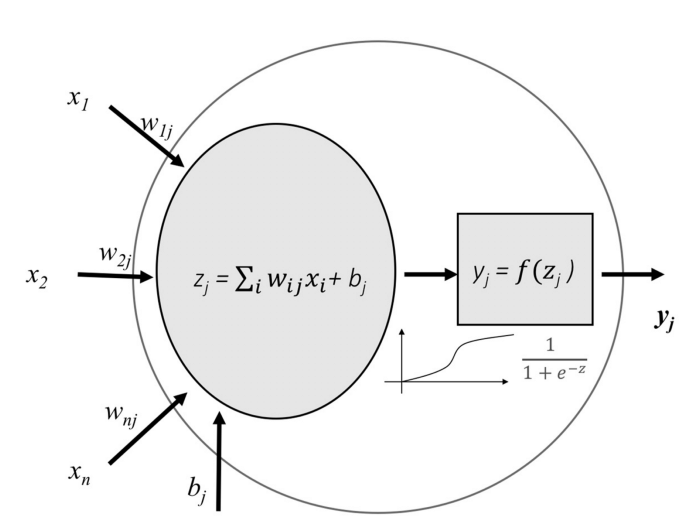
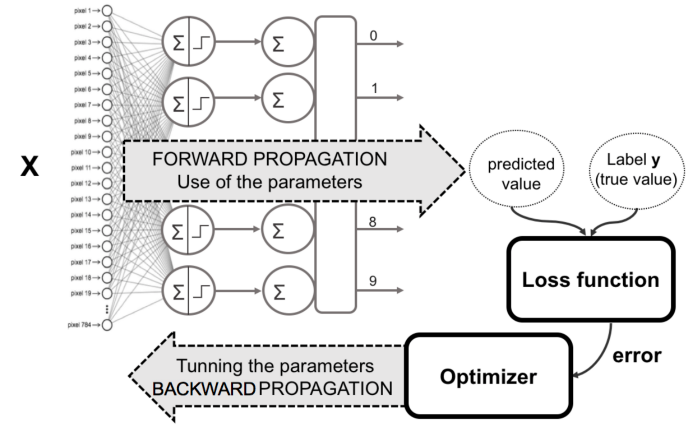
신경망 훈련은 다음과 같은 기본 단계로 구성됩니다.

1. 신경망 초기화

   가중치와 편향을 초기화합니다.

2. 순방향 전파

   주어진 입력 X, 가중치 W, 편향 b를 사용하여 모든 계층에 대해 입력과 가중치(Z)의 선형 조합을 계산한 다음 선형 조합(A)에 활성화 함수를 적용합니다.

   마지막 계층에서 $f(A^{(l-1)})$ sigmoid (이진 분류 문제의 경우), softmax (다중 클래스 분류 문제의 경우)가 될 수 있습니다.

3. 손실 함수 계산

   손실  함수는 표현식에 실제 레이블 $y$와 예측 레이블 $\hat{y}$을 모두 포함합니다. 실제 예측과 우리의 예측이 얼마나 멀리 떨어져 있는지 보여주고, 우리의 주요 목표는 손실 함수를 최소화하는 것입니다.

4. 역전파

   역전파 에서는 $y$ 및 $\hat{y}$의 함수인 손실 함수의 기울기와 $dA$, $dW$ 및 $db$ 라고 하는 기울기 $W$ 및 $b$를 찾습니다.

   이러한 gradient를 사용하여 마지막 레이어에서 첫 번째 레이어로 매개변수 값을 업데이트합니다.

5. 반복 (n epoch)

   training data를 과적합하지 않고 손실 함수가 최소화되는 것을 확인 할 때까지 n epoch 동안 2-4단계를 반복합니다.

최상의 구성을 찾는데 네 가지 주요 전략이 있다고 합니다.

• Babysitting (a.k.a Trial & Error)
• Grid Search
• Random Search
• Bayesian Optimization

Babysitting은 학문 분야에서 시행 착오 또는 Grad Student Descent(대학원생 강하 - 언어 유희인듯ㅋㅋㅋ)이라고 합니다.

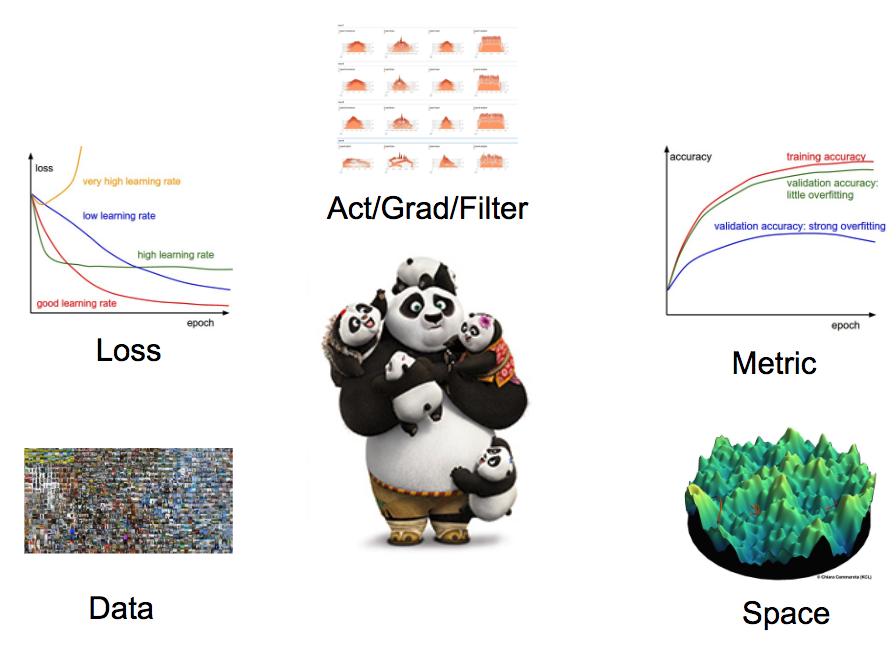
이때 질문 하나가 나옵니다.

• 최적의 하이퍼 파라미터를 찾는데 시간을 투자하는 것보다 더 좋은 방법이 있습니까?

그 방법으로

• Grid Search
• Random Search
• Bayesian Optimization

이 세 가지가 제안되고 있습니다. 위 두 가지는 강의에서 내용이 다뤄졌습니다.

하나씩 살펴보겠습니다.

Grid Search의 경우, 차원이 커질수록 차원의 저주에 빠지게 됩니다.

더 많은 차원을 추가할수록 검색하는데 시간 복잡도가 폭발하면서 이 전략을 실행 불가능하게 만듭니다.

차원이 4보다 작거나 같을 때 grid를 사용하는 것이 일반적이며, 마지막에 최상의 값을 찾는다고 하더라도 권장되진 않습니다.

대신에 Random Search를 사용합니다.

Grid Search와 Random Search의 유일한 실제 차이점은 strategy cycle의 step 1에 있다는 것입니다.

Random Search는 구성 공간에서 무작위로 포인트를 선택합니다.

이 이미지는 두 개의 하이퍼파라미터 공간에서 최상의 구성을 검색하여 두 가지 접근 방식을 비교합니다.

또한, 한 매개변수가 다른 매개변수보다 더 중요하다고 가정합니다.

Grid Layout에서는 9개의 모델을 학습시켰지만 변수당 3개의 값만 사용했음을 쉽게 알 수 있습니다!

반면 Random layout을 사용하면 동일한 변수를 두 번 이상 선택할 가능성이 극히 낮습니다.

두 번째 접근 방식이 각 변수에 대해 9개의 다른 값을 사용하여 9개의 모델을 훈련하게 됩니다.

이미지의 각 레이아웃 상단에 있는 공간 탐색에서 알 수 있듯이 Random Search(특히 더 중요한 변수의 경우)을 통해 하이퍼파라미터 공간을 더 광범위하게 탐색했습니다.

이렇게 하면 더 적은 수의 반복으로 최상의 구성을 찾는 데 도움이 됩니다.

Summary

Grid

- Bad on high spaces
+ It will find the best (but with high cost!)

Random

- It doesn't guarantee to find the best hyperparameters
+ Good on high spaces
+ Give better results (w.r.t Grid) in less iterations

Step 2: Choose the arcitecture:

say we start with one hidden layer of 50 neurons:

loss가 0에 근접하고 training accuracy가 1에 근접했으므로 overfitting이 일어났다고 볼 수 있음

• Backpropagation이 동작을 잘하고 있다.

• Weight update도 잘하고 있다

• learning rate도 괜찮다.

• learning_rate=1e-6인 경우

→ cost가 거의 감소하지 않음
→ learning rate가 너무 작다.

• Notice train/val accuracy goes to 20% though, what’s up with that?

remember this is softmax

• loss not going down: learning rate too low
• loss exploding: learning rate too high

Hyperparameter Optimization

coarse -> fine cross-validation in stages

1. First stage: only a few epochs to get rough idea of what parameters work
2. Second stage: longer running time, finer search
   … (repeat as necessary)

Hyperparameters to play wuth:

• network architecture
• learning rate, its decay schedule, update type
• regularization (L2/Dropout strngth)

Monitoring

1. loss
2. accuracy
   • big gap = overfitting
     • increase regularization strength?
   • no gap
     • increase model capacity
3. Weight updates / Weight magnitudes

Summary

We looked in detail at:

• Activation Functions (use ReLU)
• Data Preprocessing (images: subtract mean)
• Weight Initialization (use Xavier init)
• Batch Normalization (use)
• Babysitting the Learning process
• Hyperparameter Optimization
  (random sample hyperparams, in log space when appropriate)

강의 슬라이드를 바탕으로 내용을 요약하면 이렇습니다.

해당 내용에 대해 더 정리하고 싶은 부분은 dying ReLU, Batch Normalization, Bayesian Optimization 파트입니다.

cs231 강의 흐름을 바탕으로 하나씩 깊게 보려니 되게 오래 걸리네요.

이번엔 영어 자료를 바탕으로 참고하여 정리해서 뒤죽박죽이네요🤣 내용 지적도 환영입니다.