저는 해당 책으로 파이썬 기초를 꾸준히 공부 중이며, 마지막 연습문제 파트를 풀면서 부족한 부분 개념을 정리하면서 해당 책으로의 공부를 마무리에 도전합니다!😣

Q5 피보나치 함수

첫 번째 항의 값이 0이고 두 번째 항의 값이 1일 때, 이후에 이어지는 항은 이전의 두 항을 더한 값으로 이루어지는 수열을 피보나치 수열이라고 한다.

0, 1, 1, 2, 3, 5, 8, 13, ...

입력을 정수 n으로 받았을 때, n 이하까지의 피보나치 수열을 출력하는 함수를 작성해 보자.

문제 풀기 전에

💡 피보나치 수열에 대해 아시나요?

[https://news.samsungdisplay.com/23402/]

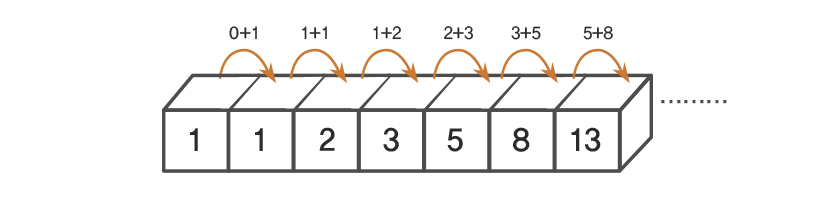
피보나치 수열은 해당 그림처럼 제일 초깃값 1에 1을 더한 값이 2, 1과 2를 더한 값 3, 2와 3을 더한값 5, ... 이런식으로 계속 끊임없이 늘어나는 수열입니다.

이 수열을 출력하는 함수를 어떻게 만들 수 있을까요?

일단 설명에서 나왔던 것처럼

• 초깃값 = 1이 있어야 할 것 같고 그 다음에 더해주는 값=1이라는 기준이 필요할 것 같습니다 그래야 1+1=2로 시작을 할테니까요.

이를 함수로 표현하면

• f(1) = 1
• f(2) = 1
• f(3) = 2
• f(4) = 3
• f(5) = 5
• f(6) = 8
  ...

이며 f(n-2;>0)-f(n-1;>0) = f(n)

그러면 이 아이디어를 갖고 함수를 만들어 봅시다.

방법 1

def fibo(n):	
	if n == 1 or n == 2:
    	return 1
    else:
    	return fibo(n-1) + fibo(n-2)

print(fibo(5)) # 5가 나옴

for i in range(10):
	print(fibo(i)) # 0, 1, 1, 2, 3, 5, 8, 13, ...

이런식으로 피보나치 수열을 표현하였습니다.

이 방식은 찾아보니까 Recursive Function이라고 합니다. 이는 재귀함수를 사용한 방식이라고도 하는데요. 자기가 자기 자신을 호출했기 때문에 그렇게 표현했고, 여기서는 무한 루프에 빠지기 쉽기 때문에 return이 중요합니다.

구박사님께 여쭤보면 파이썬으로 피보나치 수열을 표현하는 아주 많은 방법이 무수하게 나오는데요... 하나씩 살펴볼까요?

방법 2

초깃값 세팅 후 반복하면서 (이전값)+(전전값)을 더하는 방식입니다.

def fibo(n):
    a = 1
    b = 1
    if n == 1 or n == 2:
    	return 1
    for i in range(1, n):
    	a, b = b, b + a
    
    return a
    
print(fibo(5))

이 경우

for i in range(1,5)가 됩니다.

4번

• a , b = 1, 1+1로 a, b는 각각 1, 2가 됩니다.
• a , b = 2, 2+1로 a, b는 각각 2, 3이 됩니다.
• a , b = 3, 3+2로 a, b는 각각 3, 5이 됩니다.
• a , b = 5, 5+3로 a, b는 각각 5, 8이 됩니다.

여기서 return a이므로 a인 5의 값이 나오게 됩니다. 피보나치 수열의 특징은 항상 이전 값이 default로 나오기 때문에 값이 잘 나왔다는 걸 알 수 있습니다.

방법 3

def fibo():
    a, b = 0, 1
    while True:
    	a, b = b, a + b
        yield a
        
f = fibo()
next(f)

해당 방법은 제너레이터 구현 방식이라고 하는데 배우지 않아서 일단 정리만 하고 넘어가겠습니다!

결괏값으로 1이 출력됩니다.

방법 4

def fibo(n):
    fibList = [1,1]
    if n == 1 or n == 2:
    	return 1
    for i in range(2, n):
    	fibList.append(fiblist[i-1] + fibList[i-2])
        return fibList
        
print(fibo(5)) # [1, 1, 2, 3, 5]

결괏값으로 리스트에 담겨서 나옵니다.

방법 5

이번에는 람다 함수를 이용한 1줄 코딩입니다!

fibo = lambda n: 1 if n <= 2 else fibo(n-1) + fibo(n-2)

print(fibo(5)) # 5

이 코드는 정말 대박인 것 같습니다. 머릿속에 있던 게 이렇게 깔끔하게 표현되다니...!

n이 1, 2일 경우에 1의 값을 가지며, 그 외(else)에는 fibo(n-1) + fibo(n-2)의 값을 가지는 람다 함수가 만들어졌습니다.

방법 6

람다 함수를 사용하는 또다른 예제입니다.

fibo = lambda n, a=0, b=1 : a if n <= 0 else fibo(n-1, b, a+b)

print(fibo(1)) # 5

방법 7

선형대수학을 사용하는 방식입니다.

A = np.matrix([1,1], [1,0])
print(A**5)[0,1]

의 방식이라고 합니다.

이 방식들에 대한 설명은 피보나치(Fibonacci) 수열을 구현하는 7가지 방법 - 파이썬(Python) 피보나치 구현 7선 해당 글을 참고해주세요!

직접 구현하고 싶으면 실습 코드 구현해보기 이곳으로 가서 한 번 여러 가지 값을 넣어 돌려보는걸 추천드립니다!