머신러닝 sklearn.metrics 평가 지표

목차

• Confusion Matrix
• Accuracy
• Precision
• Recall
• Precision-Recall 그래프
• Average Precision (AP)
• F1 Score
• ROC와 AUC

Confusion Matrix

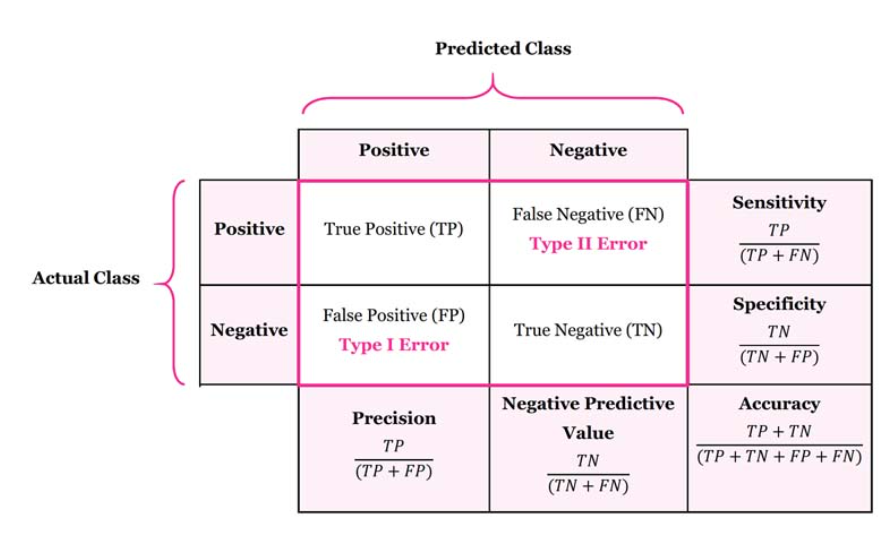
• Confusion Matrix란? 실제 라벨(Actual Class)과 예측 라벨(Prediction) 일치하는 개수를 matrix로 표현하는 기법

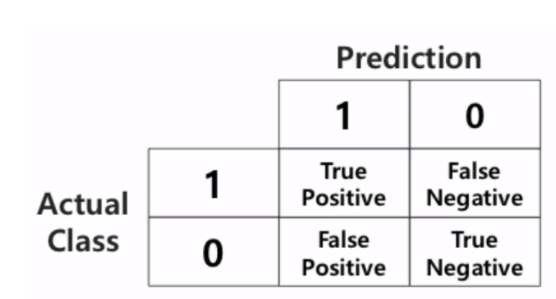
Actual Class & Prediction 의 조합으로 표현

1. TP(True Positive) : Positive로 예측해서 True임

• True : 예측이 맞음
• Positive : 예측값이 Positive(1)

2. FP(False Positive) : Positive로 예측해서 False임

• False : 예측이 틀림
• Positive : 예측값이 Positive(1)인 경우 (즉, 실제값은 거짓(0)입니다.)

3. FN(False Negative) : Negative로 예측해서 False임

• False : 예측이 틀림
• Nagative : 예측값이 Negative(0)인 경우 (즉, 실제값은 참(1)입니다.)

4. TF(True Negative) : Negative로 예측해서 True임

• True : 예측이 맞음
• Negative : 예측값이 Negative(0)인 경우

Accuracy

• 전체 대비 정확히 예측한 개수의 비율

• ACC = $\frac {TP+TN}{TP+TN+FP+FN}$

• ACC = 1 - ERR

• 불균형한 데이터셋에서 Accuracy를 사용한다면 결과는 상당히 왜곡됩니다. 예를 들어, 시험 합격률이 2%일 때, 모든 수험자가 불합격한다고 예측하면 98%의 정확도를 가지기 때문에 정확도는 높지만 쓸모 없는 모델이 만들어 집니다.

• 이때, Accuracy 대신 사용할 수 있는 지표가 Precision과 Recall입니다.

Precision

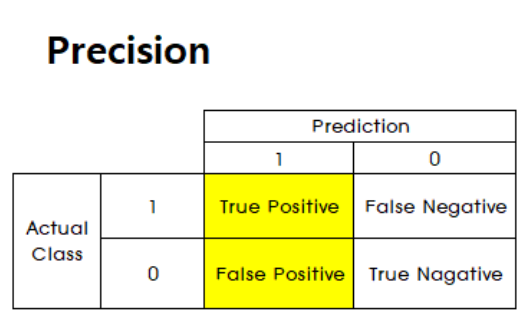
• Precision은 positive라고 예측한 비율 중에 실제로 positive인 비율을 나타냅니다.

• 즉, 얼마나 잘 예측하였는지를 알려주는 지표입니다.

• Precision = $\frac {TP}{TP+FP}$

Recall

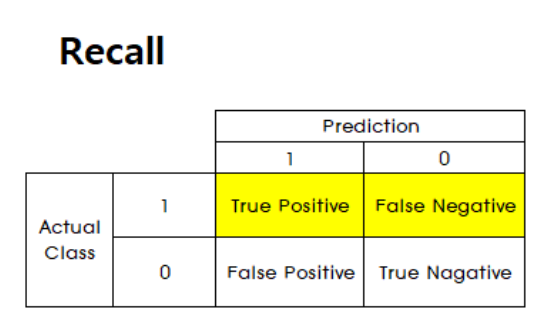
• 실제 positive 데이터 중 positive라고 예측한 비율을 뜻합니다.

• precision의 기준은 모델이 '예측'한 것인 반면, Recall의 기준은 '데이터'입니다.

• 따라서 실제 positive한 것 중에서 얼마나 잘 예측하는지 비율을 Recall이라고 해석하면 됩니다.

• Recall = $$\frac {TP}{TP+FN}$

Precision-Recall 그래프

Precision과 Recall의 상관관계를 나타내는 그래프

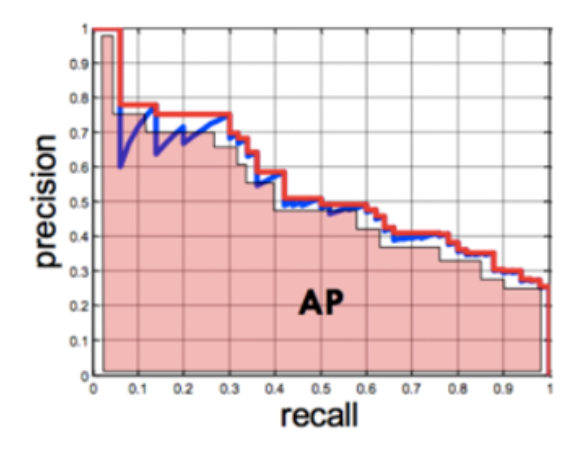
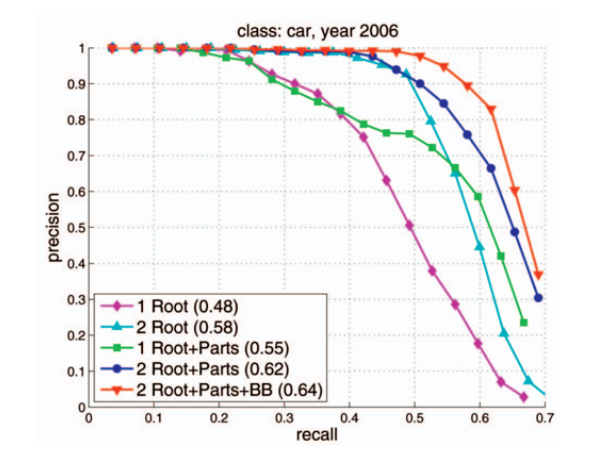
Average Precision (AP)

• Precision-Recall 그래프는 어떤 알고리즘의 성능을 전반적으로 파악하기에는 좋으나 서로 다른 두 알고리즘의 성능을 정량적으로 비교하기에는 불편함
• 따라서 Average Precision을 비교하면 용이함
• Precision-Recall 그래프에서 그래프 선 아래쪽의 면적을 계산하는 방식
• 면적의 값이므로 AP가 클수록 성능이 좋은 알고리즘이라 볼 수 있음

F1 Score

• Precision과 Recall은 서로 trade-off 관계를 가지면서 접근하는 방식도 Precision은 모델의 예측, Recall은 정답 데이터 기준이므로 서로 상이함
• 하지만 두 지표 모두 모델의 성능을 확인하는데 중요하므로 둘 다 사용되어야 함
• 따라서 두 지표를 평균값을 통해 하나의 값으로 나타내는 방법을 F1-score라고 함
• 이때, 사용되는 방법은 조화평균이다.
• 조화평균의 사용 이유는 평균이 Precision과 Recall 중 낮은 값에 가깝도록 만들기 위함
• 조화평균의 경우, 평균 계산에 사용된 값이 불균형할 수록 페널티가 가해져서 작은 값에 가깝도록 평균이 계산됨

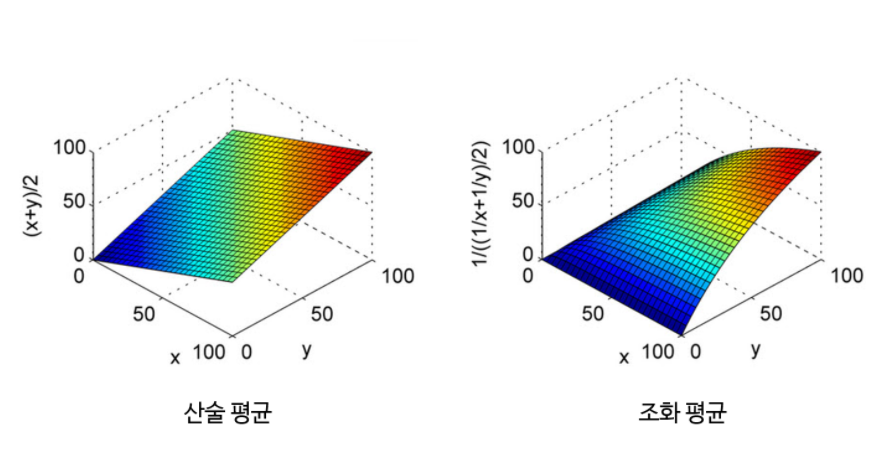
• X, Y 값 차이가 크면 Z 축의 값이 작음

• 따라서 극단적으로 Precision과 Recall 중 한쪽이 1에 가깝고 한쪽이 0에 가까운 경우, 산술 평균과 같이 0.5가 아니라 0에 가깝도록 만들어줍니다. 따라서 F1 score를 높이게 하려면 Precision과 Recall이 균일한 값이 필요하기 때문에 두 지표 성능 모두를 높일 수 있도록 해야 함

• F1-score = $$\frac 2{precision x recall}{precision+recall}$

• 물론 데이터셋마다 특성이 다르므로, precision, recall, F1 score를 비교하며 가장 적합한 것을 사용해야 함

ROC와 AUC