다익스트라 vs 벨만-포드

• 다익스트라는 모든 가중치가 양수인 경우에만 사용할 수 있다.
• 벨만-포드는 노드 간의 간선 가중치가 음수인 경우에도 사용할 수 있다.
• 다익스트라는 시간 복잡도가 빠르지만, 벨만-포드는 시간 복잡도가 느리다. (V: 정점의 수, E: 간선의 수)
  • 다익스트라의 시간 복잡도 : O((V+E) log V)
  • 벨만 포드의 시간 복잡도 : O(V*E)
• 다익스트라는 매번 방문하지 않은 노드 중 최단 거리가 가장 짧은 노드를 선택한다.
• 벨만-포드는 매번 모든 간선을 전부 확인하면서 최단 거리를 구한다.

다익스트라

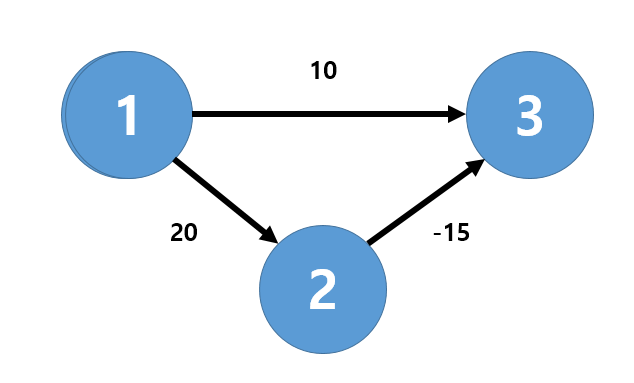
• 다익스트라의 경우에는 최단 경로를 (1) -> (3)으로 선택할 것이다.
  • 매번 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 먼저 선택하여 나아가기 때문에

예를 들어, 각 간선을 아래와 같이 A, B, C라고 하자.
A가 10, B가 20, C가 -15이고, 시작점이 1인 경우에 다익스트라로 풀게 되면 A의 가중치 < B의 가중치이므로 큐에 3번을 먼저 넣고, 그 다음으로 2번을 넣을 것이다.

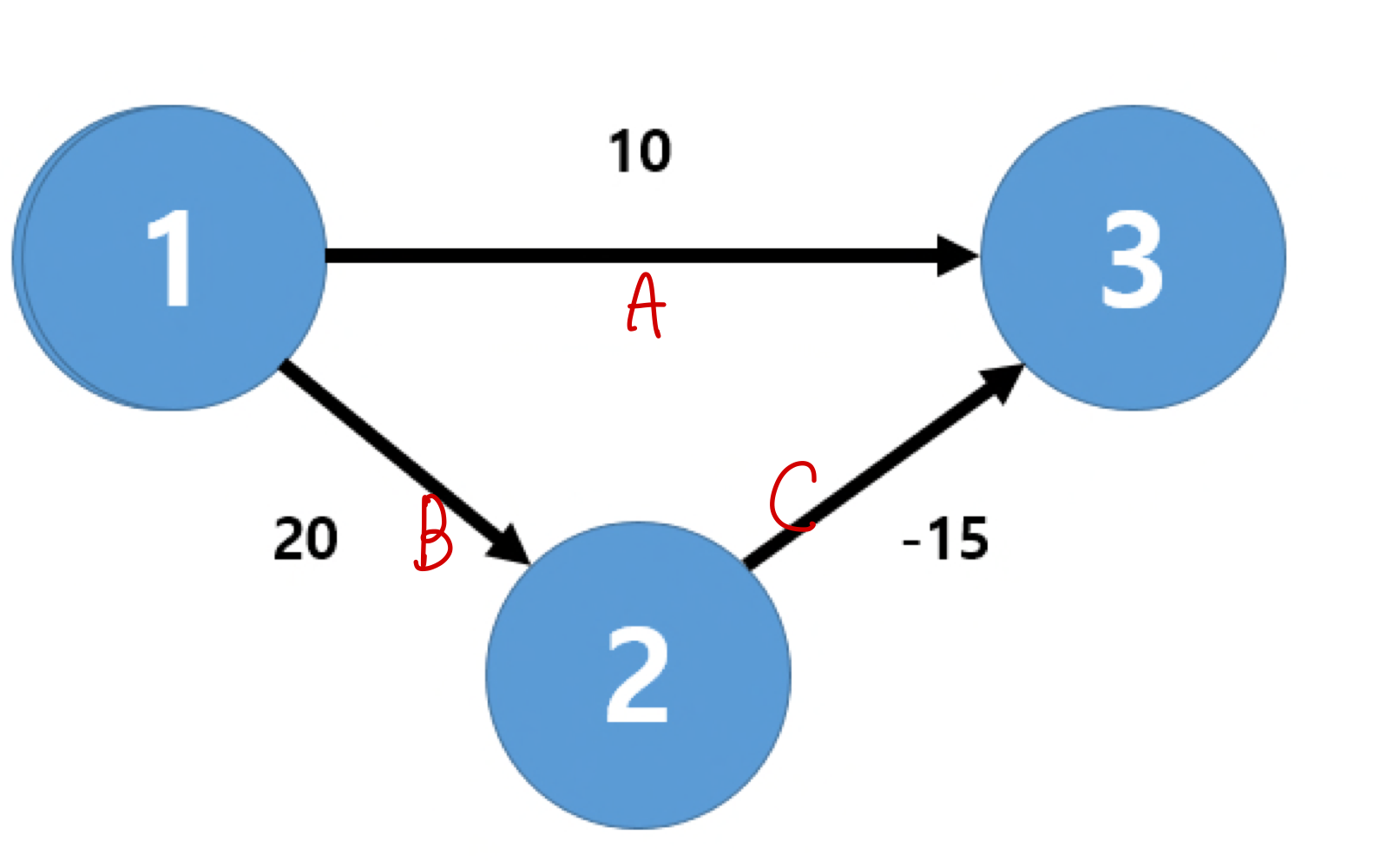
3번 노드는 이미 visited = True가 되어, 2번 -> 3번 경로는 신경쓰지 않을 것이다.
다익스트라는 모든 가중치가 양수라고 가정하기 때문이다.
C의 가중치가 양수이면, A의 가중치 < B의 가중치인 상황에서 A의 가중치 < B의 가중치 + C의 가중치는 당연하기 때문에 이미 방문한 노드의 다른 경로는 보지 않는 것이다.

하지만 C의 가중치는 음수이기 때문에 잘못된 최단 거리를 찾게 된다.

벨만 포드

• 벨만 포드의 경우에는 최단 경로를 (1) -> (2) -> (3)으로 선택할 것이다.
• 벨만 포드를 사용하면, 매번 모든 간선을 전부 확인한다.

---

벨만-포드 알고리즘

• 한 정점으로부터 다른 모든 정점까지의 최단 경로를 구하는 알고리즘

1. 모든 간선이 양수인 경우
2. 음수 간선이 있는 경우
   2-1. 음수 간선 순환은 없는 경우
   2-2. 음수 간선 순환이 있는 경우

• 벨만-포드 알고리즘은 모든 경우에 사용이 가능하다. 하지만 (1)번의 상황에서는 다익스트라를 사용하는 것이 더 효율적이다.

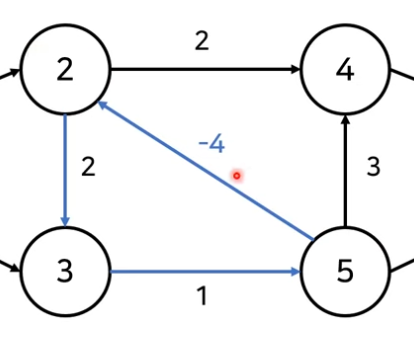
❗️ 음수 간선의 순환이 있는 경우를 주의해야 한다!
음수 간선의 순환(2 + 1 + (-4) = -1) 을 계속 돌게 되면, 최단 거리는 음의 무한이 되기 때문에

구현

1. 시작 노드의 거리를 0으로 초기화, 나머진 노드는 거리를 무한으로 초기화한다.
2. 정점 수 -1(V-1) 만큼 다음 과정을 반복
   2-1. 전체 간선(E개)를 하나씩 확인한다.
   2-2. 각 간선을 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신한다.
   ( dist[인접 노드] > dist[현재 노드] + 간선 가중치 )
3. 음수 간선 순환이 발생하는지 확인하려면, 2번의 과정을 한번 더 수행한다.(V 번째 반복)
   V번째 반복에서도 최단 거리 테이블이 갱신된다면, 음수 간선 순환이 존재하는 것!

V-1번

[참고]
벨만-포드 알고리즘 1
벨만-포드 알고리즘 2
https://stalker5217.github.io/algorithm/bellman-ford/
https://www.youtube.com/watch?v=Ppimbaxm8d8&ab_channel=%EB%8F%99%EB%B9%88%EB%82%98