AVL 트리는 자기 균형 이진 탐색 트리(Self-balancing Binary Search Tree) 의 한 종류이다.
자기 균형 이진 탐색 트리란?
데이터를 삽입하거나 삭제해도 트리의 높이가 일정 수준 이상으로 자라지 않도록 자동으로 균형을 유지하는 이진 탐색 트리(Binary Search Tree, BST)이다.
이진 탐색 트리 (BST) 란?
각 노드가 최대 2개의 자식을 가지는 트리
왼쪽 자식 < 부모 < 오른쪽 자식
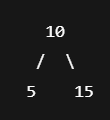
그런데 균형이 깨지게 될 경우
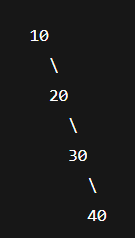
이진 탐색 트리의 규칙은 지켰지만 한쪽으로 치우쳐져
트리 높이가 O(n) → 성능이 선형 탐색 수준으로 느려진다.
이러한 단점을 보완한 것이 자기 균형 트리이다.
자기 균형 이진 탐색 트리의 예시로
| 종류 | 특징 |
|---|---|
| AVL 트리 | 높이 기준으로 엄격한 균형 유지 |
| 레드-블랙 트리 | 색깔 규칙으로 느슨한 균형 유지 |
| Splay 트리 | 최근 사용된 노드를 루트로 끌어올림 |
| B 트리 | 디스크 기반 시스템에서 사용 (파일 시스템 등) |
이런 트리들이 있는데 오늘은 AVL 트리에 대해 알아보자.
AVL 트리의 가장 큰 특징은 모든 노드에 대해 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이가 1 이하로 유지되도록 하는 것 이다.
-
각 노드는 균형 인수(Balance Factor) 를 가진다.
Balance Factor = 왼쪽 서브트리 높이 - 오른쪽 서브트리 높이 -
값이 -1, 0, 1 이면 균형 상태
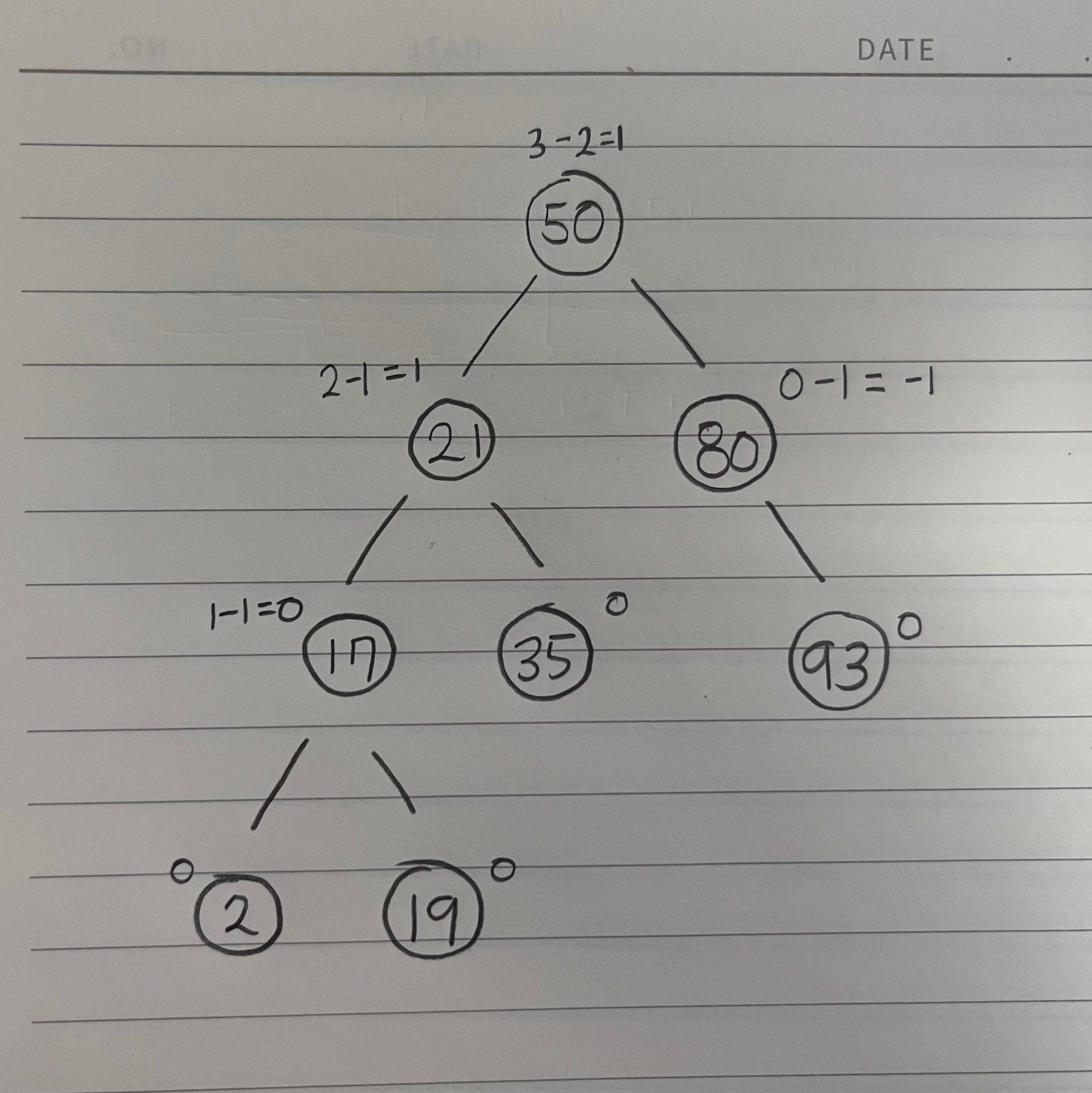
균형 상태를 이룬 AVL 트리이다!
균형 인수 역시 사진 처럼 계산하면 된다.
회전 (rotation)
검색 및 순회 연산은 BF를 변경하지 않지만 삽입 및 삭제에서는 BF가 변경될 수 있다.
삽입 삭제 시 불균형 상태가 되면 AVL트리는 불균형 노드를 기준으로 서브트리의 위치를 변경하는 rotation 작업을 수행하여 트리의 균형을 맞추게 된다.
LL 회전 (단순 오른쪽 회전)
왼쪽 자식의 왼쪽 서브트리에 삽입
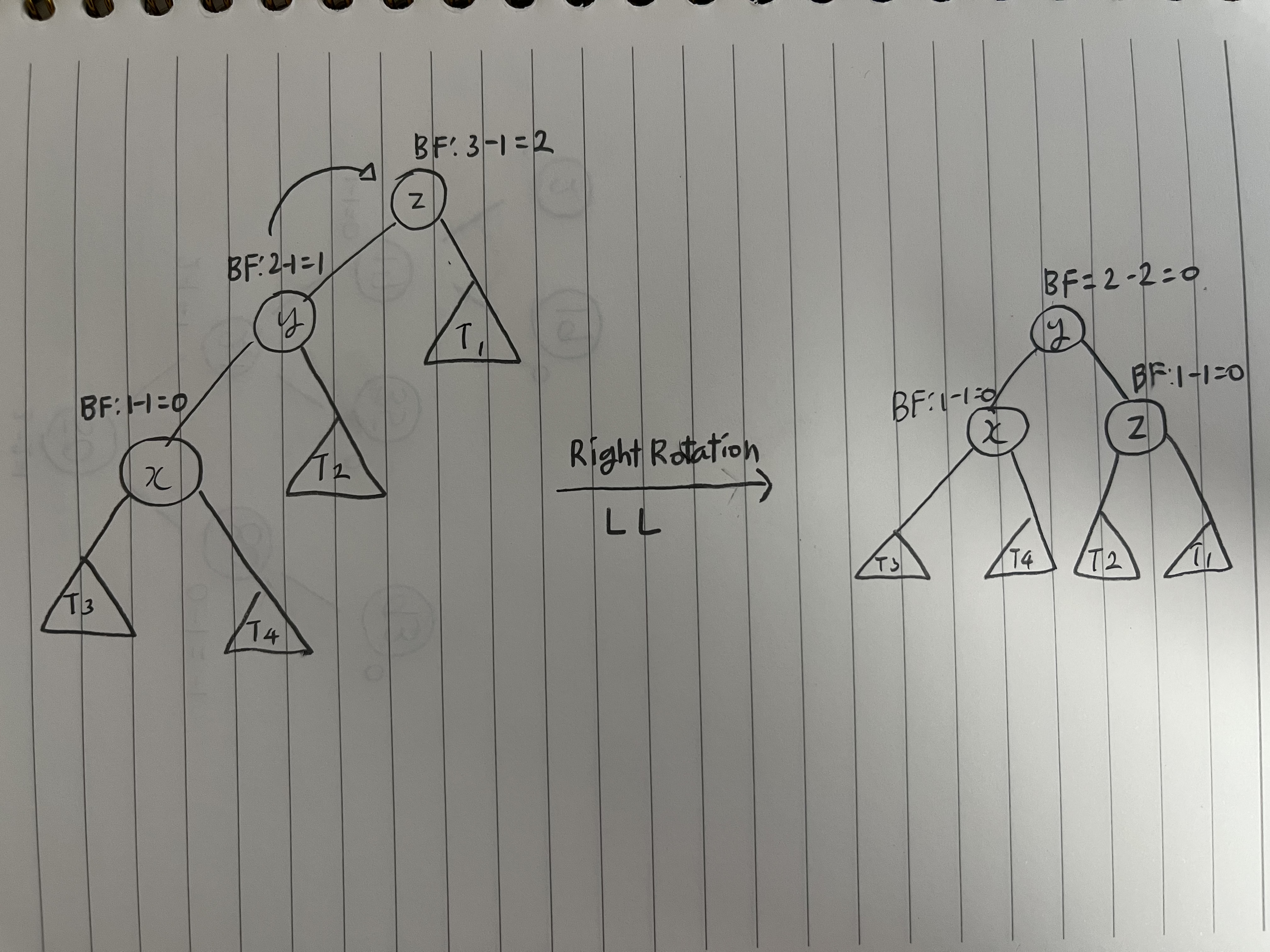
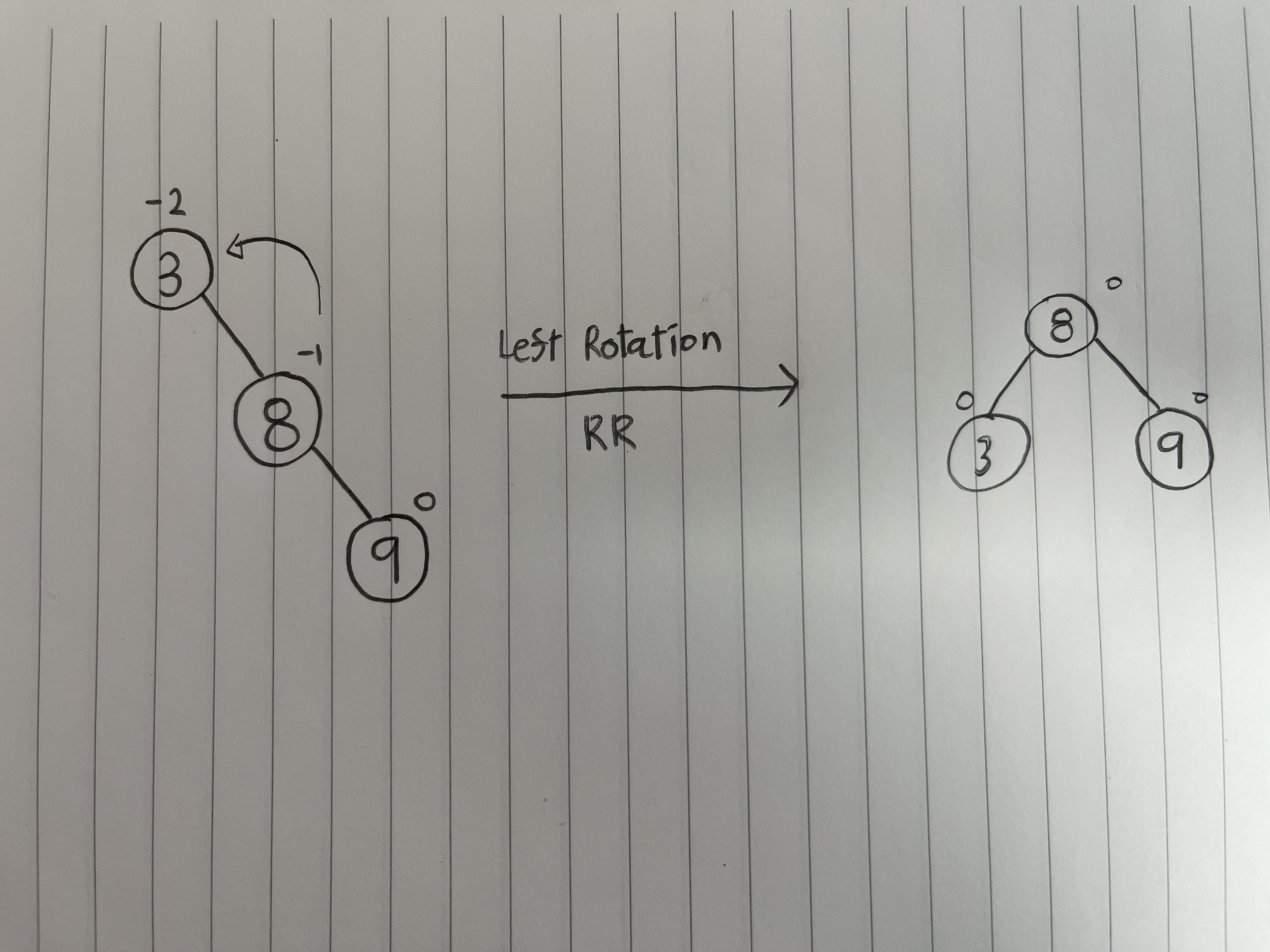
RR 회전 (단순 왼쪽 회전)
오른쪽 자식의 오른쪽 서브트리에 삽입
LR 회전 (왼쪽-오른쪽 회전)
왼쪽 자식의 오른쪽 서브트리에 삽입
RL 회전 (오른쪽-왼쪽 회전)
오른쪽 자식의 왼쪽 서브트리에 삽입
AVL 트리 vs 레드-블랙 트리
| 항목 | AVL 트리 | 레드-블랙 트리 |
|---|---|---|
| 균형 유지 방식 | 높이 균형 (Balance Factor) | 색상 기반 균형 (Red/Black) |
| 검색 속도 | 더 빠름 (더 엄격한 균형 유지) | AVL보다 느림 |
| 삽입/삭제 성능 | 회전이 더 자주 발생 → 느림 | 회전이 적음 → 빠름 |
| 구현 복잡도 | 상대적으로 복잡 | 상대적으로 단순 |
| 트리 높이 | O(log n), 평균 낮음 | O(log n), 평균 높음 |
AVL 트리는 왜 STL 컨테이너에 채택되지 않았을까?
STL의 std::map, std::set 등은 내부적으로 레드-블랙 트리(RB 트리) 를 사용한다.
삽입/삭제 속도 차이
-
AVL은 더 자주 회전을 필요로 하기 때문에 삽입/삭제 연산에서 느림
-
STL 컨테이너는 삽입/삭제가 잦은 경우가 많음 → RB 트리가 적합
복잡성
-
AVL은 균형 조건이 엄격해서 코드가 더 복잡
-
STL 라이브러리에서는 성능 + 간결한 구현이 중요
실용적인 효율성
-
AVL이 검색에서 약간 빠르지만, 삽입/삭제에서의 손해가 더 큼
-
RB 트리는 전체적으로 더 일관된 성능을 보장
