
그래프
- 그래프(Graph)는 데이터 간의 관계를 표현하기 위한 자료구조입니다.
- 그래프는
비선형 구조이며,트리의 일반적인 개념입니다.- 트리도 일종의 그래프 중 하나에 속합니다.
- 현상이나 사물을
정점과간선으로 표현한 것이다.정점: Vertex, 대상이나 개체간선: Edge, 정점 간의 관계가중치: Weight, 간선의 크기가 있는 경우
- 그래프 G를 보통 G=(V, E)로 표시한다.
- 정점의 총 수 :
|V| - 정점 u와 정점 v를 잇는 간선 :
{u, v}
그래프의 종류

무방향 그래프- (간선의) 방향이 없는 그래프
방향 그래프- 방향성이 있는 그래프
가중치 그래프- 간선의 가중치값이 존재하는 그래프
루트없는 트리- 간선을 통해 정점 간 잇는 방법이 한가지인 그래프(*트리의 정의)
이분 그래프- 그래프의 정점을 겹치지 않게 두 그룹으로 나눈 후 다른 그룹끼리만 간선이 존재하게 분할할 수 있는 그래프
사이클이 없는 방향 그래프- 정점에서 출발해 자기 자신으로 돌아오는 경로(사이클)가 없는 그래프
그래프의 표현
- 그래프도 트리처럼 가장 대표적인 연산이
모든 정점을 탐색하는 것입니다. - 단, 그래프는 추상적인 개념이므로 코드상으로 어떻게 표현하는지부터 이해하는 것이 좋습니다.

-
크게
인접 행렬과인접 리스트로 2가지 방법으로 분류할 수 있습니다. -
인접 행렬- 2차원 배열로 정점 간의 간선의 존재 여부를 1 또는 0으로 표현
- 행렬에서 0이 아닌 원소의 수는 간선 총 수의 2배 입니다.
- 행렬 표현법은 이해하기 쉽고 간선의 존재 여부를 즉각 알 수 있습니다.
- n*n 행렬이 필요하므로
n²에 비례하는 공간이 필요합니다. - 행렬의 준비 과정에서 Θ(n2)의 시간 필요합니다.
- 즉, 연결되지 않은 간선들도 확인해야 하기 때문에 느립니다.
- 간선의 밀도가 아주 높은 그래프에 적합합니다.
- 간선의 밀도가 높지 않은 경우 공간 낭비가 심합니다.
-
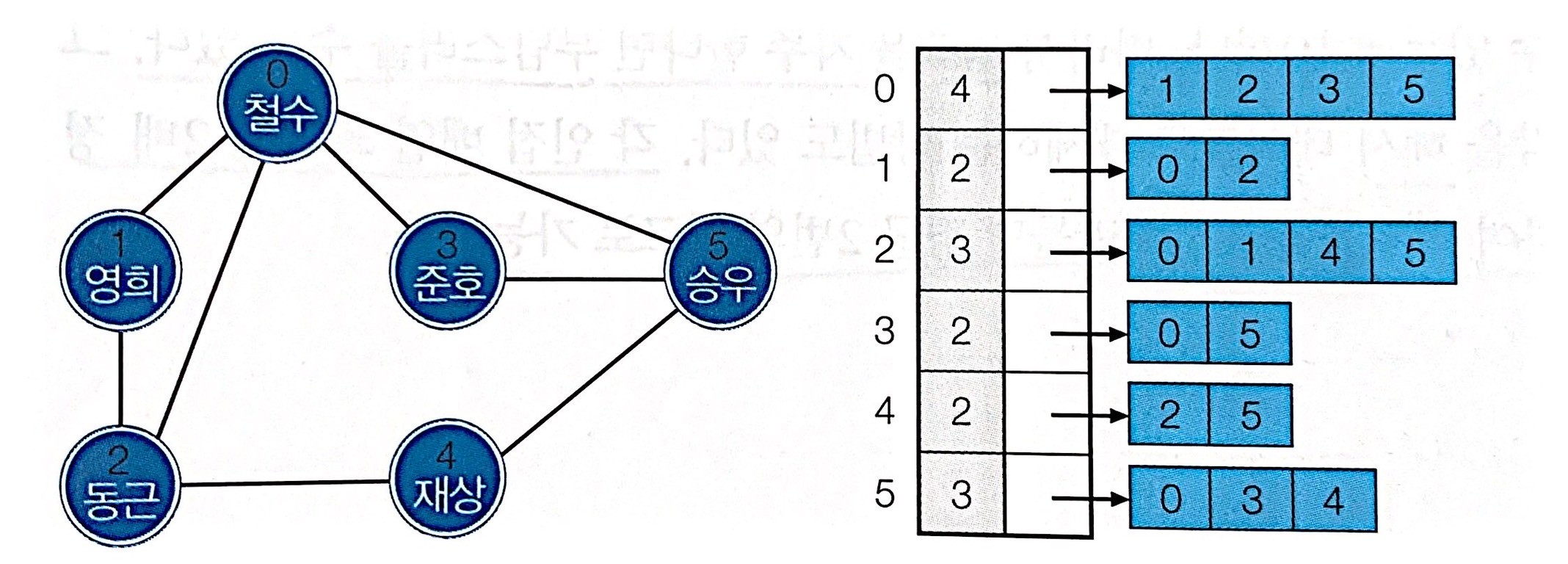
인접 리스트- 정점 개수만큼 리스트를 만들어 각각의 정점 리스트에 간선 추가
- 존재하지 않는 간선은 리스트에 나타나지 않습니다.
무방향 그래프를 위한 인접 리스트 표현에서필요한 총 노드 수는 총 간선 수의 2배 입니다.- 공간이 간선의 총 수에 비례하는 양만큼만 필요하므로 대체로 행렬 표현에 비해 공간의 낭비가 없습니다.
- 정점 i와 정점j 간에 간선이 존재하는지 알아볼 때 인접 행렬 표현보다 시간이 많이 걸린다.
- 특히 간선이 많다면 인접성을 한 번 체크하는데만 최악의 경우 n에 비례하는 시간이 들 수 있습니다.
- 따라서, 간선의 밀도가 아주 높은 경우
인접 행렬방식을 쓰는 것이 낫습니다.
- 따라서, 간선의 밀도가 아주 높은 경우
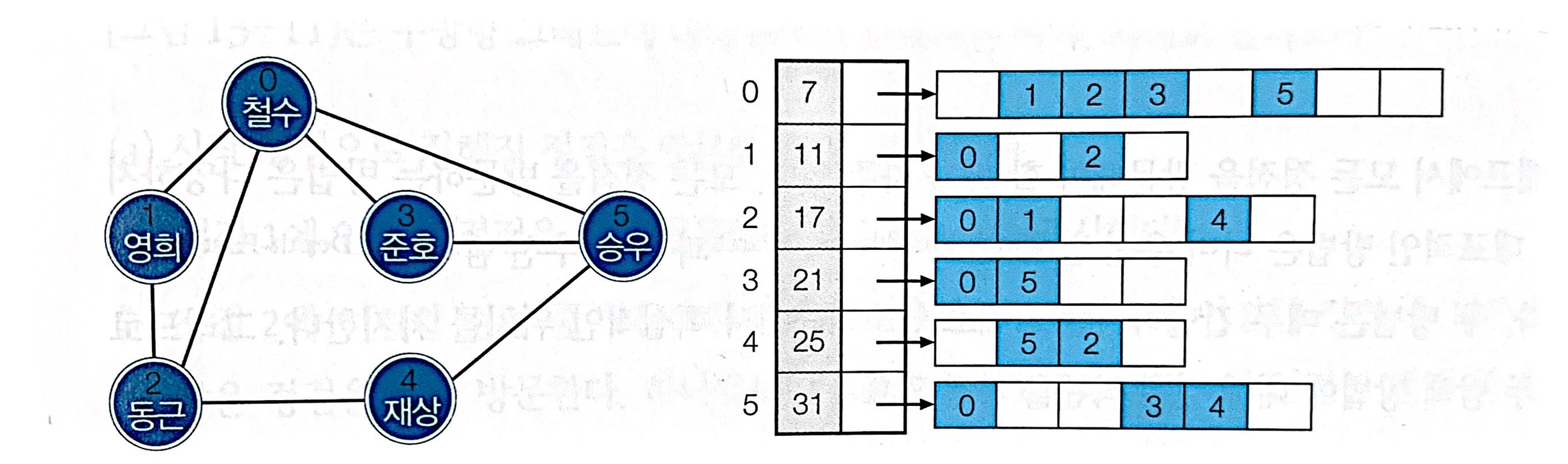
인접 배열- 두 정점 간 간선 존재 여부를 체크하는 일이 잦으면 수행시간에 큰 부담을 주는 기존 위에 두 방법에 비해 인접 리스트처럼 간선의 수에 비례하는 공간을 쓰면서 인접 리스트보다 간선의 존재 여부를 훨씬 빠르게 체크할 수 있는 방법입니다.
- 리스트 대신 배열로 저장하여 연결 리스트의 링크를 위한 공간을 절약할 수 있을 뿐더러 노드들이 메모리에 흩어져서 존재하는 불안감으로부터 벗어날 수 있습니다.
- 알고리즘 입장에서 보면
정적 (static)입니다.- 그래프가 한번 만들어진 후 변하지 않는 경우에 적합합니다.
- 배열 내에서
이진 탐색 가능합니다.- ⎣log₂k⎦ 1 번 이내의 비교로 두 노드가 인접한지 확인 가능합니다.
인접 해시 테이블- 다루어야 할 그래프가 엄청난 크기인 경우 이진 탐색을 한다고해도 검색을 자주 하기 만만치 않은데, 인접 배열을 각각 해시 테이블로 대체하는 방법으로 해소가 가능하다.
- 각 인접 배열 크기의 2배 정도 되는 공간을 할당하여 적재율을
0.5로 만들면 평균 2번의 비교로 가능하다. - 임의의 정점에 인접한 모든 다른 정점에 순차적으로 접근해야 하는 경우, 불편하다.
너비 우선 탐색과 깊이 우선 탐색
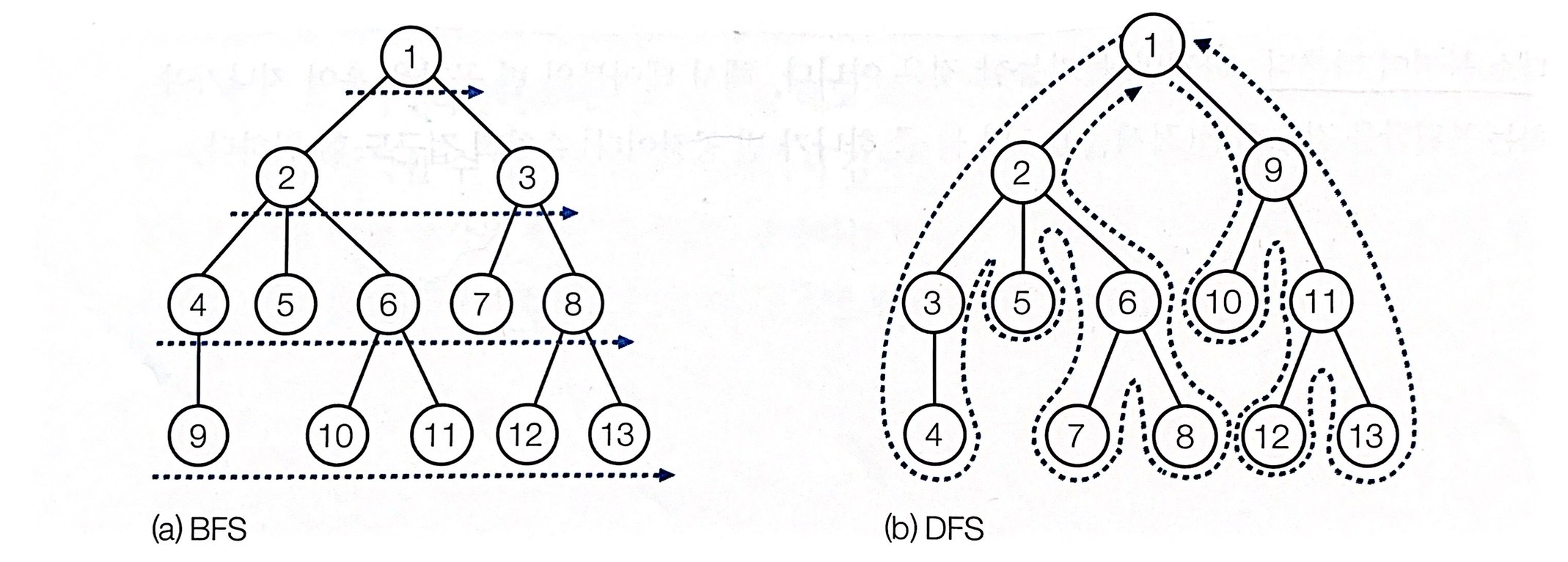
- 그래프에서 모든 정점을 방문해야 할 때가 자주 있는데,
탐색에 대표적인 방법은너비 우선 탐색과깊이 우선 탐색이다.
너비 우선 탐색 (BFS)

- 그래프 G가 2개 이상으로 끊겨 있으면 모든 정점을 방문하기 위해서는 여
러 번 BFS를 수행할 수 있습니다. G = (V, E) 에서의 BFS 수행 시간- Θ(V+E), Θ(|V|+|E|)
- 모든 정점을 방문하고 각 정점에 연결된 정점을 방문
(a) 시작 정점으로 정해진 정점을 방문한다.
(b) 정점 1에 인접한 정점을 모두 방문한다. (각각 2, 3, 4로 표시했다.)
(c) 정점 2에 인접한 정점 중 방문하지 않은 정점은 없다. 정점 3에 인접한 정점 중 방문하지 않은 정점을 모두 방문한다. 하나밖에 없다(5로 표시했다.). 정점 4에 인접한 정점 중 방문하지 않은 정점을 모두 방문한다. 2개가 있다.(각각 6, 7로 표시했다.)
(d) 정점 5에 인접한 정점 중 방문하지 않은 정점은 없다. 정점 6에 인접한 정점 중 방문하지 않은 정점을 모두 방문한다. 하나밖에 없다.(8로 표시했다). 정점 7에 인접한 정점 중 방문하지 않은 정점은 없다.
(e) 마지막으로 정점 8에 인접한 정점 중 방문하지 않은 정점이 없어 더 이상 갈 곳이 없으므로 끝낸다.
BFS 알고리즘BFS(G, s): for each v ∈ V-{s} v.visited 🠔 NO s.visited 🠔 YES enqueue(Q, s) while (Q != Ø) u 🠔 dequeue(Q) for each v ∈ u.adj if (v.visited = NO) v.visited 🠔 YES enqueue(Q, v)
깊이 우선 탐색 (DFS)
G = (V, E) 에서의 DFS 수행 시간- Θ(V+E), Θ(|V|+|E|)
- 모든 정점을 방문하고 각 정점에 연결된 정점을 방문
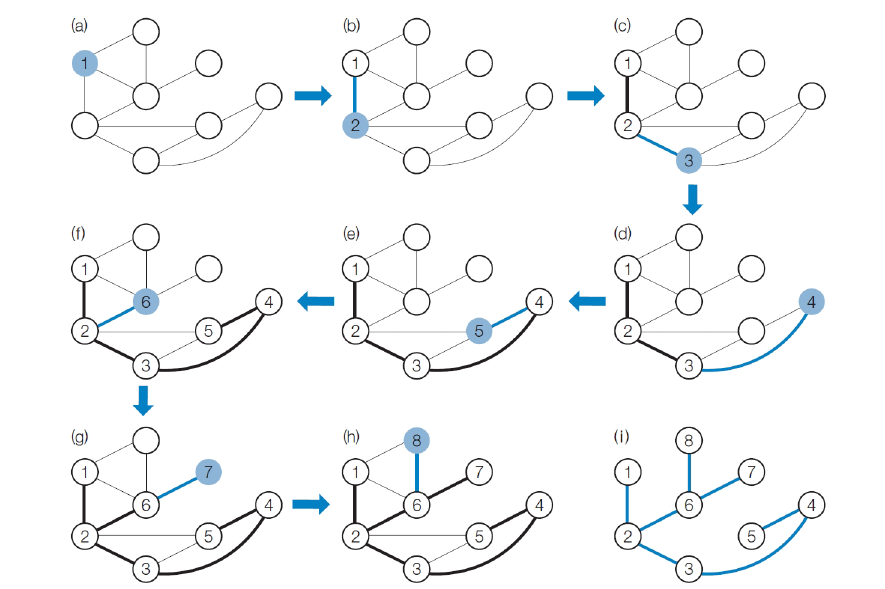
(a) 시작 정점으로 정해진 정점을 방문한다. (1로 표시했다.)
(b) 정점 1에 인접한 정점 중 하나를 방문한다. (2로 표시했다.)
(c) 정점 2에 인접하면서 방문하지 않은 정점은 총 3개다. 이 중 하나를 방문한다. (3으로 표시했다.)
(d) 정점 3에 인접하면서 방문하지 않은 정점은 총 2개다. 이 중 하나를 방문한다. (4으로 표시했다.)
(e) 정점 4에 인접하면서 방문하지 않은 정점은 총 하나뿐이다. 이 곳을 방문한다. (5으로 표시했다.) 5에 인접한 정점 중 방문하지 않은 정점은 없다. 따라서 왔던 길로 되돌아간다. 정점 4, 3, 2로 되돌아가는 과정에 정점 4, 3에 인접한 정점 중 방문하지 않은 정점은 없다.
(f) 정점 2로 되돌아가면 이에 인접한 정점 중 방문하지 않은 정점이 하나 있다. 이곳을 방문한다. (6으로 표시했다.)
(g) 정점 6에 인접한 정점 중 방문하지 않은 정점은 총 2개다. 이 중 하나를 방문한다. (7으로 표시했다.)
(h) 정점 7에 인접한 정점 중 방문하지 않은 정점은 없다. 정점 6으로 돌아간다. 정점 6에 인접한 정점 중 방문하지 않은 정점이 하나 있다. 이곳을 방문한다(8로 표시했다.). 정점 8에서 인접한 정점 중 방문하지 않은 정점은 없다. 정점 6으로 돌아간다. 정점 6에서도 인접한 정점 중 방문하지 않은 정점은 없다. 정점 2로 돌아간다. 정점 2에서도 방문하지 않은 정점은 없다. 정점 1로 돌아간다. 정점 1에서도 방문하지 않은 정점은 없다. 시작 정점(정점1)에서 더 이상 갈 곳이 없으므로 끝낸다.
DFS 알고리즘DFS (G, v): v.visited 🠔 YES for each x ∈ v.adj if (x.visited = NO) DFS(G, x)
최소 신장 트리 (Minimum Spanning Tree)

연결 그래프 (Connected Gratph)- 간선의 방향이 없는 그래프에서 모든 정점들 간에 간선을 따라 서로 다다를 수 있는 그래프이다.
- 연결 그래프를 만들기 위한 최소 간선의 수 :
|V| - 1
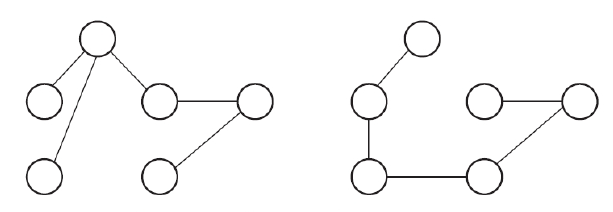
신장 트리 (Spanning Tree)- 트리는
"싸이클이 없는 연결 그래프”로 정의 - 최소한의 간선 |V|-1을 사용하면서 연결된 그래프를 신장 트리 (Spanning Tree) 라고 한다.
- 하나의 그래프에서 신장 트리는 여러 형태가 될 수 있다.
- 트리는
최소 신장 트리 (Minimum Spanning Tree)- 간선의 가중치 합(Cost)이 최소가 되도록 하는 신장 트리이다.
- 가중치가 있는 무향 그래프에서 적용
프림 알고리즘 (Prim Algorithm)
- 아무 간선도 없는 상태에서 간선을 하나씩 더하는 작업을
|V|-1수행

O(ElogV)- 최소 값을 가지는 간선을 찾는 시간
- 최소 힙을 사용하는 경우
O(logV)
- 최소 힙을 사용하는 경우
- 모든 노드에 대해 연결된 간선을 살펴보며 비용을 업데이트
- 힙의 조정 연산 E회 발생
- 최소 값을 가지는 간선을 찾는 시간
크루스칼 알고리즘 (Kruskal Algorithm)
- 간선이 하나도 없는 상태에서 간선을 하나씩 추가
여러정점 집합으로 시작하여 집합을 합쳐 나감

O(ElogV)- 간선 정렬 시간이 시간복잡도 결정:
O(ElogE)=O(ElogV) - 이후에는 최소 값을 가진 간선을 차례대로 제거하며 집합 정보 업데이트:
O(E + VlogV)- 집합 정보 처리에 대한 시간 복잡도는 향후 알고리즘에서 다루는 주제
- 간선 정렬 시간이 시간복잡도 결정:
위상 정렬 (Topological Sorting)
- 상후 선후 관계가 존재하는 작업을 정렬하기



조건- 싸이클이 없는 방향 그래프
위상 순서- 간선 (x→y)가 존재하면 정점 x는 정점 y에 앞선다.
- 대개 한 방향 그래프에는 서로 다른 위상 순서가 여러개 존재한다.
위상 정렬(Topological Sorting)- 주어진 방향 그래프 G의 위상 순서 중 하나를 찾는다.
Θ(V+E)의 시간 복잡도- 모든 정점을 방문하며 그 때마다 연결된 간선을 모두 제거
- 간선은 단 한번씩만 취급
최단 경로
- 출발지부터 도착지까지 최단 시간이 소요되는 경로 구하기
- 그래프에서 경로를 구성하는 가선들의 가중치 합이 해당 경로의 길이
최단 경로를 구하는 알고리즘 종류
다익스트라 알고리즘벨만-포드 알고리즘- 하나의 시작 정점으로부터 다른 모든 정점에 이르는 최단 경로 구함.
쌍최단 경로 알고리즘- 모든 정점 쌍 간의 최단 경로를 구하는 알고리즘
다익스트라 알고리즘
- 모든 간선 가중치가 음이 아닌 일반적인 경우에 사용한다.

- 그래프 G = (V, E)에서 간선들의 가중치가 모두 0 이상이다.
- 최소 신장 트리를 위한
프림 알고리즘과 원리 유사하다.- 경로에 포함된 노드부터 도달 가능한 노드 중에 가장 가중치가 작은 노드를 선택한다.
- 새로운 노드가 선택됨에 따라 경로 비용 갱신한다.
- 모든 노드가 경로에 포함되면 완료한다.
욕심 (Greedy) 알고리즘으로 최적해 보장한다.
벨만-포드 알고리즘
- 다익스트라 알고리즘은 음의 가중치가 있는 경우 해결하지 못한다.
- 음의 가중치가 필요한 경우 :
- 최단 경로를 구하는 대신 거쳐 가면 좋을 장소가 있는 경우 (해변도로)
- 네트워크에서 데이터 패킷의 경로 계산 할 때 (트래픽을 분산 목적 등)
- 간선을 최대 1개 사용하는 경우, 최대 2개 사용하는 경우, … 최대 n-1개 사용하는 경우의 최단 경로를 구해 나가며 최종적인 최단 경로를 구한다.
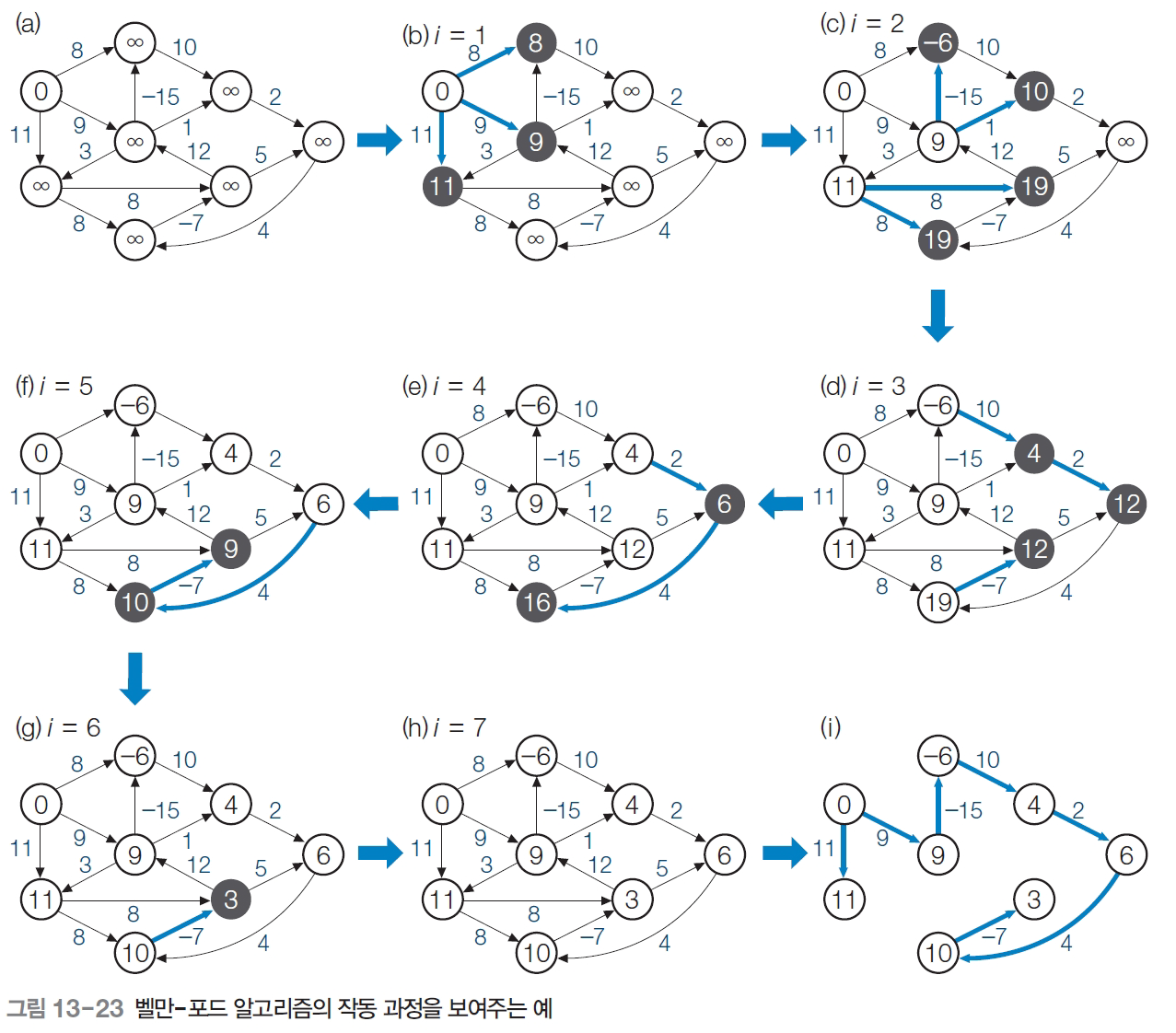
음의 싸이클은 허용하지 않는다.





