퍼셉트론이란?

퍼셉트론

다수의 신호를 입력으로 받아 하나의 신호를 출력한다.

퍼셉트론은 두 가지의 값을 가지는데, 1과 0으로 가진다.

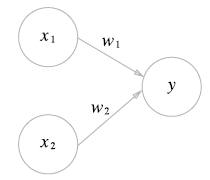
퍼셉트론은 입력 신호 x와 출력 신호 y, 가중치 W를 가진다.

W는 노드라고도 부르며 흔히 뉴런이라고 부른다.

입력 신호에 뉴런이 보내질 때는 각각의 고유한 가중치가 곱해진다.

뉴런에서 보내온 신호의 총 합이 정해진 한계를 넘어설 때만 1을 출력한다.

또한 한계를 임계값이라고 하며 (Θ 세타) 라고 표현한다.

활용

AND

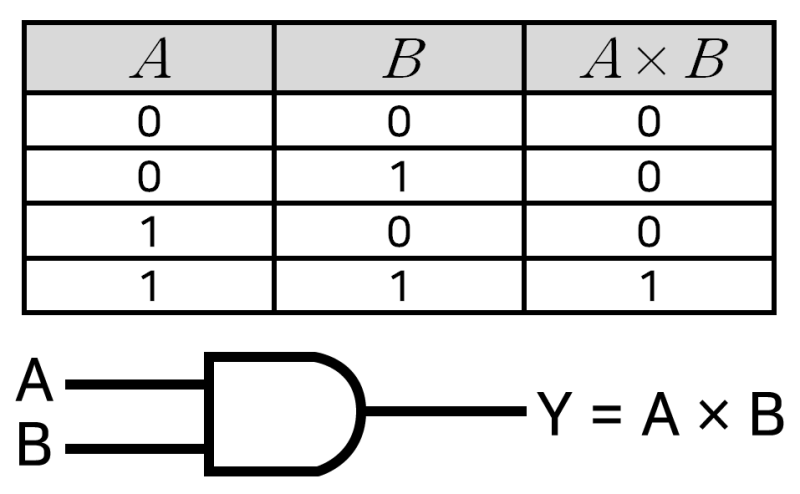
퍼셉트론을 이용해서 AND 연산을 할 수 있다. 입력 신호 x1, x2의 값을 1과 0으로
지정해준 다음 가중치 W1, W2( 가중치의 값은 임의로 정함 )를 곱하였을 때 임계값(한계) 을 넘어서면 1을 넘어서지 않으면 0을 출력하도록 한다.

def AND(x1, x2):
    W1, W2, theta = 0.5, 0.5, 0.7 # 임의로 정한 값
    tmp = x1*W1 + x2*W2 # 가중치(W)와 입력 신호(X)를 곱해서 tmp에 저장해줌 
    
    if tmp <= theta:
        print(0)
    else :
        print(1)

if __name__ == '__main__':
    AND(0,0)
    AND(1,0)
    AND(0,1)
    AND(1,1)

0
0
0
1

과 같이 출력이 되게 된다.
위의 원리는 0.5 + 0.5를 해야만 임계값(0.7)을 넘게된다.

가중치와 편향 도입

AND

앞에서 구현한 AND함수는 정말 간단하다. 하지만 조금 있으면 나올 b(편향)을 위해서 다르게 numpy를 사용해서 벡터와 배열로 정의하여 보겠다.

식은 이러하다. Y = (x1W1 * x2W2) + b

코드는 조금 전보다 달라지긴 했지만 그래도 쉽다.

import numpy as np

def AND(x1, x2):
    x = np.array([x1, x2])
    W = np.array([0.5, 0.5])
    b = -0.7

    tmp = np.sum(x*W) + b

    if tmp <= 0:
        print(0)
    else:
        print(1)

if __name__ == '__main__':
    AND(0,0)
    AND(1,0)
    AND(0,1)
    AND(1,1)

np.sum()을 사용하기 위해서 numpy를 불러왔다.

numpy는 관례적으로 np라고 쓴다.

또한 새로 생긴 편향값 b는 뉴런이 얼마나 쉽게 활성화를 하느냐를 조정하는 매개변수이다.

np.sum()은 입력한 배열에 담긴 모든 원소의 총합을 계산한다.

그럼 이제 편향값을 추가해서 NAND와 OR를 구현해 보겠다.

OR

import numpy as np

def OR(x1, x2):
    x = np.array([x1, x2])
    W = np.array([0.5, 0.5])
    b = -0.2

    tmp = np.sum(x*W) + b

    if tmp <= 0:
        print(0)
    else :
        print(1)

if __name__ == '__main__':
    OR(0,0)
    OR(0,1)
    OR(1,0)
    OR(1,1) 

0
1
1
1

tmp가 1보다 작다면 0을 출력 즉, np.sum(x*W) 를 했을 때 값이 0보다 크기만 하면 1을 출력한다.
또한 OR게이트는 편향값을 -0.2로 해주어야한다. ( XOR 게이트를 만들면서 구글링을 해본 결과 거의 모든 사람들이 OR의 편향 값을 -0.2로 하였기 때문.)

NAND

import numpy as np

def NAND(x1, x2):
    x = np.array([x1, x2])
    W = np.array([-0.5, -0.5])
    b = 0.7

    temp = np.sum(x*W) + b

    if temp <= 0:
        print(0)
    else :
        print(1)

if __name__ == '__main__':
    NAND(0,0)
    NAND(0,1)
    NAND(1,0)
    NAND(1,1)

1
1
1
0

가중치 W의 값을 -를 곱해준다.

다음은 XOR이다. 그런데 XOR은 퍼셉트론의 한계라고 볼 수 있다.

XOR을 하려면 다층 퍼셉트론이 되어야 한다. 다음에는 다층 퍼셉트론에 대해서 정리하도록 하겠다.