통계학 : 1. 데이터의 기술 => data의 특성
2. 모르는 것의 추측
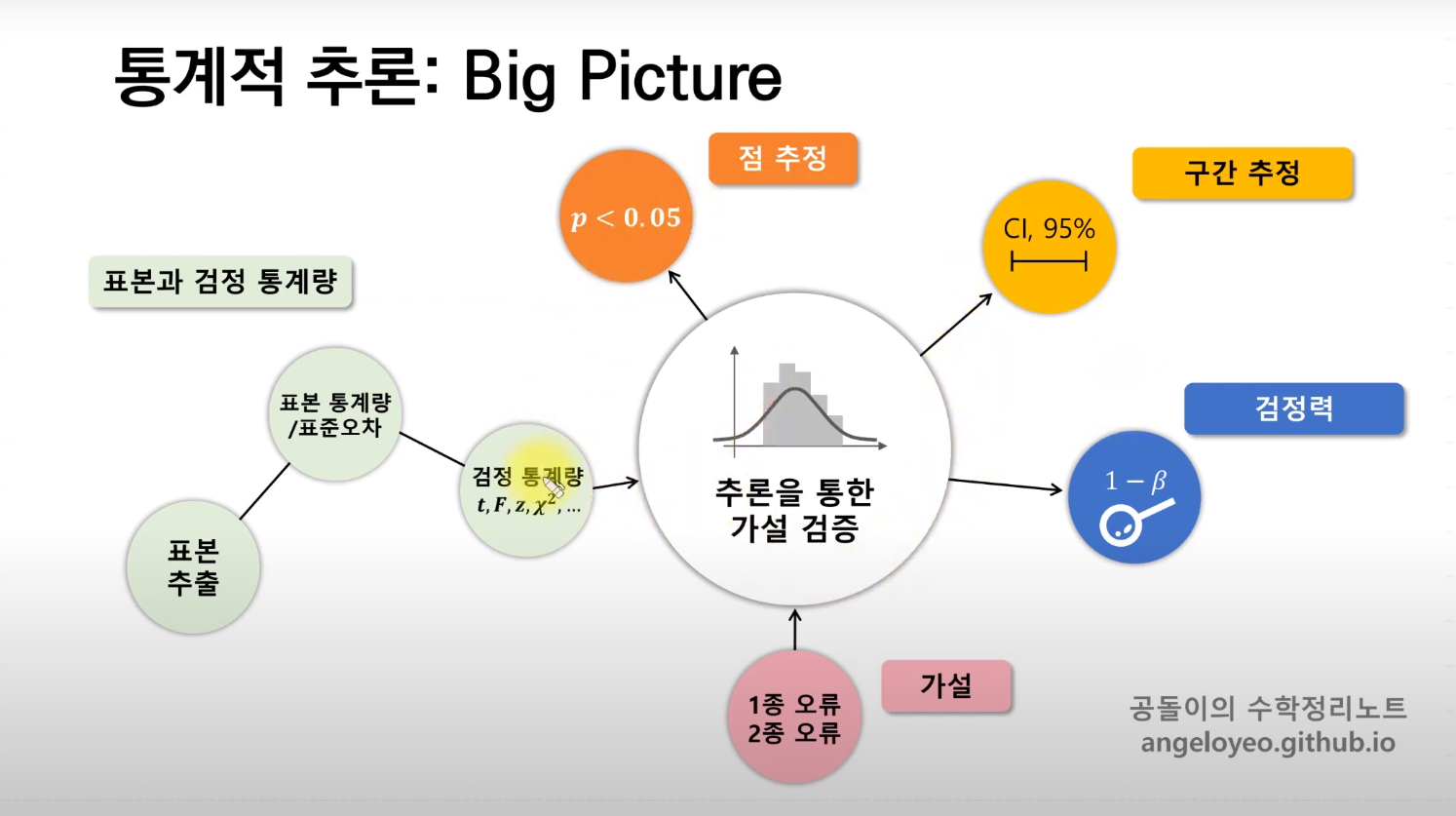
모집단과 표본 집단
- 검정을 위한 통계학
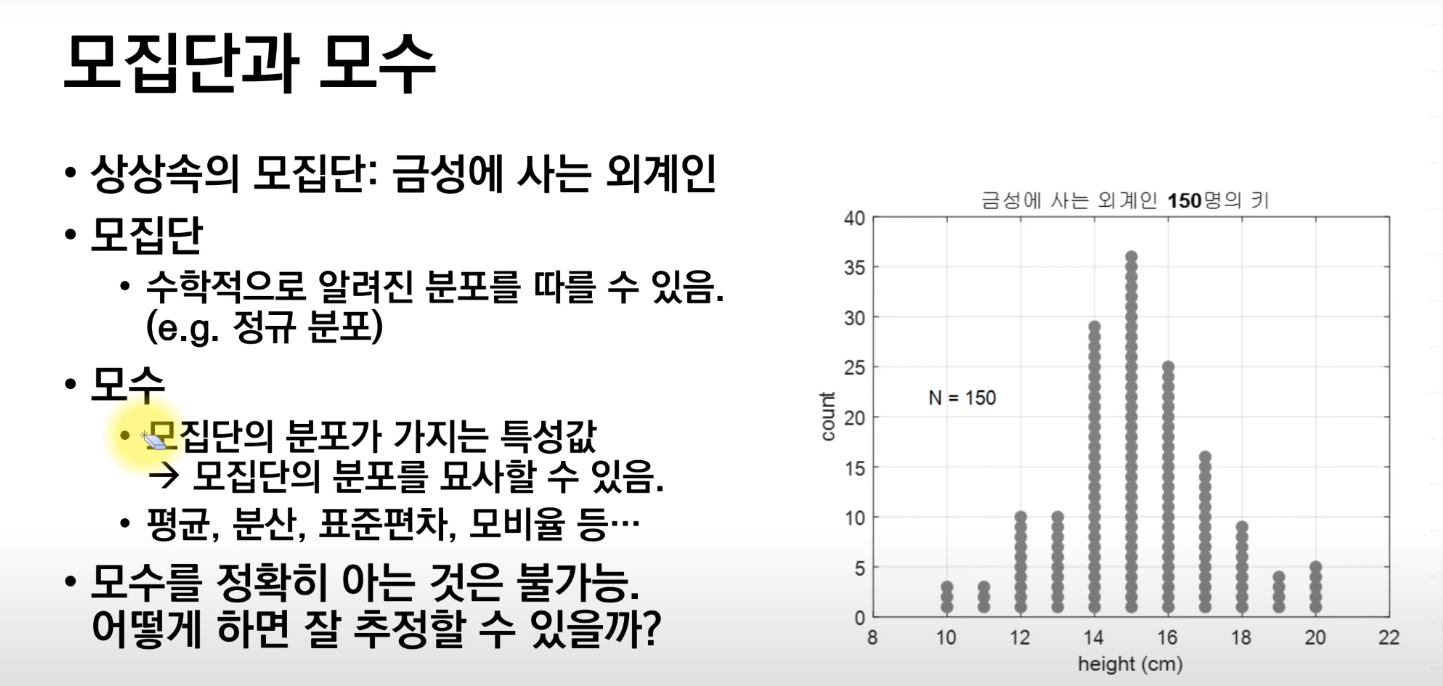
- 모수만으로도 추정이 가능, 모수를 추정하기 위함!
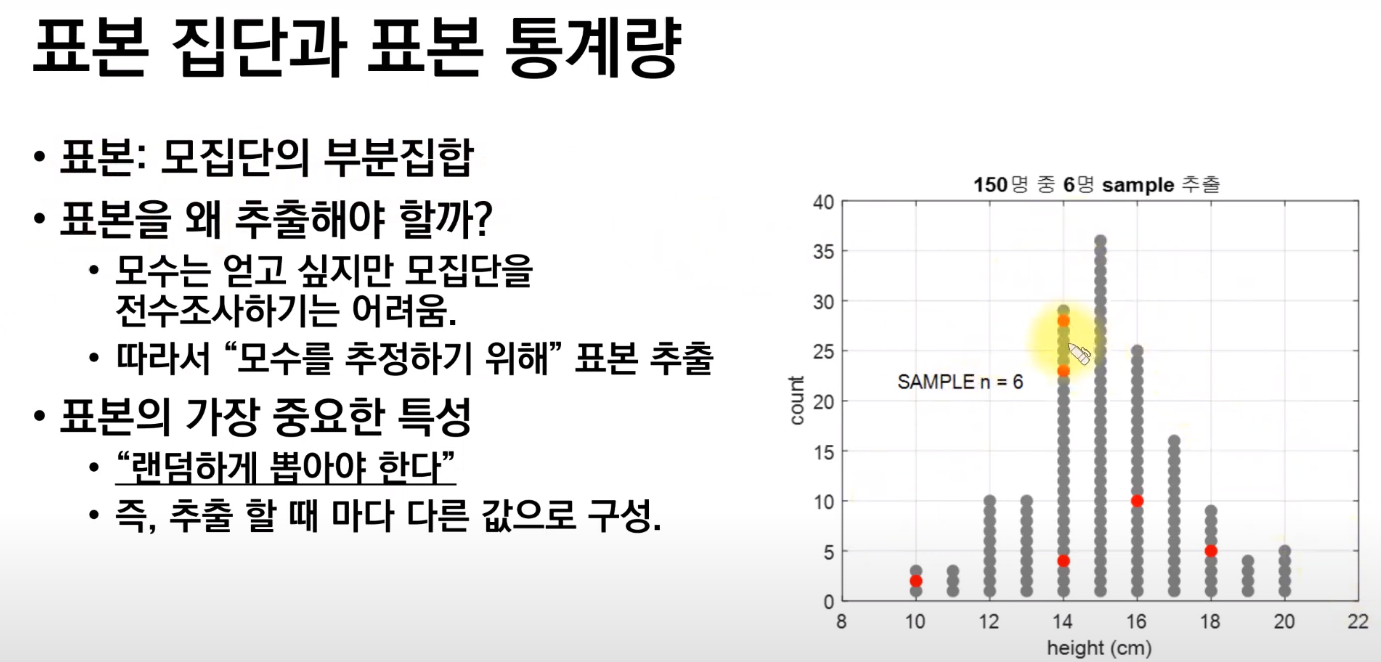
- 표본을 뽑는 이유 : 모수는 얻고 싶지만, 모집단을 통해서는 알아낼 수 없기에 random하게 뽑은 표본을 통해 추정을 한다.
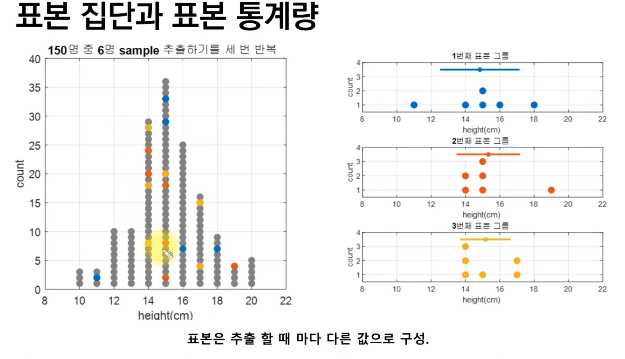
- 표본 또한 평균, 분산이 있음
=> 표본 통계량 == 모수에 대한 추정치 => 항상 오차를 수반한다! -> Standard Error


주의: 표준 오차와 표준 편차는 다른 개념이다
표본 평균 표준 오차(SEM)와 표준 편차를 혼용해서 사용하거나, 잘못 사용하는 경우가 있다.
- 특히, 논문을 보다보면 이런 실수들을 종종 찾아볼 수 있는데, 식 (8)에서 볼 수 있었듯이 SEM은 표준 편차에 비해서 항상 값이 작기 때문에 데이터를 서술할 때 더 결과가 좋아보이기 때문이다.
- 다시 한번 정리하자면 표준 편차는 모집단의 분포가 얼마나 퍼져있는가를 서술하는 개념이고, SEM은 평균의 추정치에 대한 불확실도를 수치화한것이다.
- 보통의 경우 결과를 보는 사람의 입장에서는 모집단에 관심있는 경우가 더 많으므로 데이터에 관해 기술할 때는 표준 편차(혹은 그에 준하는 추정치)를 사용해 기술해야한다.
https://www.youtube.com/watch?v=J2sv6NNu1-M&list=PL5yujGYFVt0Cr2wyzeMfBKW_Pfktcdnjr&index=9

검정 통계량
- 목적 : 통계적으로 비교 분석하기 위함
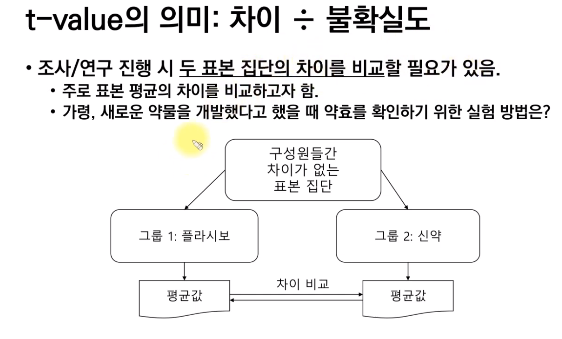
-
두 집단의 표본 평균의 차이를 비교하고자 할 때 => t - value를 검정 통계량으로 사용

t- value : 차이 / 불확실도 => 차이 x 확실성

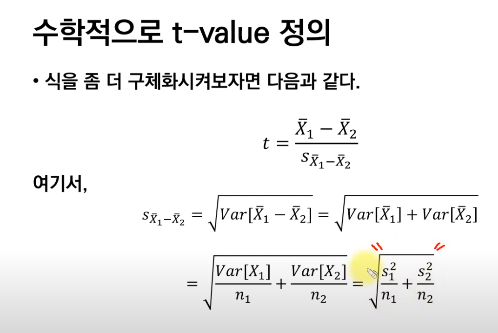
-
t - value 계산 값 > t 기준 => 차이가 난다.
-
충분히 큰 t - value : 상위, 하위 2.5%
t - test
-
두 집단의 평균이 다르다고 볼 수 있는 지 알아보는 test
-
t : 그룹 간 평균 차이가 클수록 큰 값을 가지는 수
-
그렇다면, 남자 키와 여자 키의 평균 비교 시 t 의 값은 단순히 그 평균키 값들의 차이일까? No
-
why? 표본으로부터 얻는 평균값은 항상 달라지며, 불확실성이 있고, 오차가 있음
-
표본들은 random하게 뽑혔고, 우리가 추출한 표본의 평균값 또한 random하게 얻어진 값임

-
확실도는 구할 수 없기에, 불확실도로 나누어준다!
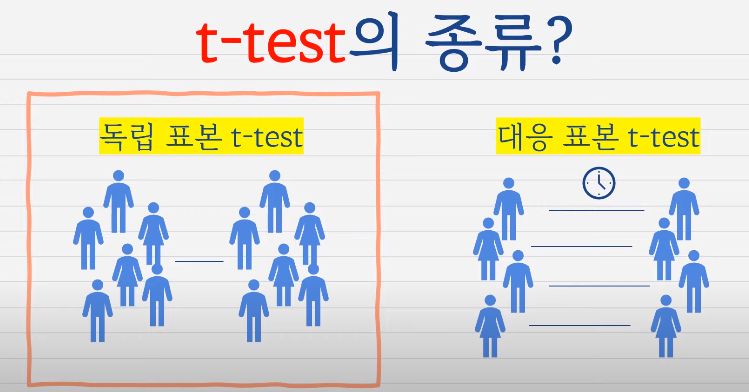
-
독립 표본 : 두 그룹의 사람들이 전혀 다른 사람들
-
대응 표본 : 두 그룹의 사람들이 같은 사람들 (before / after)
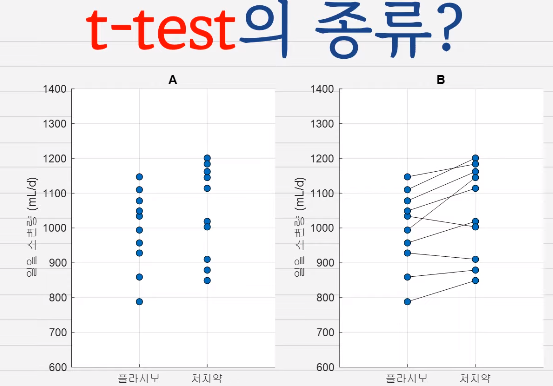
https://justdoitman.tistory.com/51
https://speedspeed.tistory.com/13
adsp
https://youtu.be/sC5kphIAMzQ?si=NEZsfdMjjoK07AI5
Q. P value 가 뭐냐? 그리고 어떻게 사용하냐?
A. P value 란 귀무가설이 맞다는 가정할때 제가 구한 통계값이 얼마나 자주 나올지를 확률로 나타낸 값입니다. 이 p value 은 귀무가설을 기각할지 말지의 여부를 결정할때 사용하며, 너무 작으면 귀무가설이 맞다는 가정이 틀렸다는 것을 알 수 있기 때문에 기각을 해 대립가설을 채택하면 됩니다.
Q. T test 가 뭐냐?
A. T test 은 두 집단의 평균이 같은지를 귀무가설로 설정해 확인하는 검정법을 말합니다.
Q. T test 의 종류에는 뭐가 있냐? 그리고 간략하게 설명해봐라.
A. T test 에는 크게 3가지가 있습니다. 단일표본 t test, 독립표본 t test, 쌍체표본 t test 가 있습니다. 단일표본 t test 은 집단이 특정 평균값 뮤와 같은지를 확인하는거고, 독립표본 t test 은 독립적인 두 집단의 값들의 평균이 같은지를 확인하는거고, 쌍체표본 t test 은 같은 표본인데 변화를 가한 우의 평균이 같은지를 확인하는 겁니다.
Q. T test 의 기본 전제가 뭐냐? 그리고 그 전제가 만족되지 않으면 어떡하냐
A. T test 은 기본적으로 모든 표본들이 정규분포를 이룬다는 가정을 합니다. 이 가정이 만족되지 않으면 t test 말고 wilcoxon test 를 실행해야 합니다.
Q. T test를 실행하는데 비교할 집단이 3개 이상이면 어떻게 할건가?
A. T test 은 두 집단을 비교합니다. 3개 이상의 집단을 비교한다면 ANOVA Analysis of Variance 를 이용해야합니다. 이 ANOVA 를 통해 구한 f value 와 p value 가 기각역보다 작으면 평균이 다른 집단이 적어도 하나가 있다는 것입니다.
Q. F test 는 뭐냐?
A. F test 은 두 집단의 분산이 다른지를 확인하는 검정입니다. 귀무가설로 '두 집단의 분산이 같다' 로 설정하고 대립가설은 '두 집단의 분산이 다르다' 로 설정을 해 수식을 통해 f value 를 구하고 f 분포표에서의 기각역에 해당되는 p value 와 비교해 귀무가설을 기각할지 말지를 결정합니다.
P value
귀무가설이 맞다고 가정할때 내가 현재 구한 통계값이 얼마나 자주 나올지 확률로 구한 것
T test
T test 정의는 '두 집단의 평균이 같은지를 확인하는 검정' 이다. 이를 하는 방법은 알맞은 t test 를 선택해 t value 를 구하고 이에 따르는 p value 를 구해 귀무가설을 기각할지의 여부를 선택하면 된다. 이때 귀무가설은 '두 집단의 평균이 같다' 이고 대립가설은 '두 집단의 평균은 다르다' 이다.
이때 t test 은 표본들이 기본적으로 정규분포를 이룬다고 할때 사용할 수 있다. 만약 정규분포를 이루지 않으면 Wilcoxon test 를 이용해야 한다.
T test 은 크게 3가지 종류가 있다.
1. 단일표본 t test, 1 sample t test
2. 독립표본 t test, unpaired t test
3. 쌍체표본 t test, paired t test
-
단일표본 t test, 1 sample t test
1 sample t test 은 '집단의 평균이 알려진 숫자 뮤와 같다' 을 실험하는 검정이다.
예시로는 '남학생 평균 키가 172이다' 의 가설을 확인하기 위해 남학생 키 1000 개를 수집해 이를 실험하는 것이다. 한개의 집단과 한개의 값을 비교. -
독립표본 t test, unpaired t test
unpaired t test 은 '두 집단의 평균이 같다' 를 실험하는 검정이다.
예시로는 'A 학교 남학생 평균 키와 B 학교 남학생 평균 키가 같다' 의 가설을 확인하기 위해 두 집단의 키 1000개를 수집해 실험하는 것이다. 두 개의 집단을 비교.
이때 독립표본 t test 은 두 집단이 서로 독립인지 아닌지를 확인해야한다. 이를 위해서 아래에 서술할 f test 를 사용하면 되는데, 이를 사용해 둘의 분산이 같게(등분산) 나타나면 독립이라 하고 진행하면 된다. 다르게(p value가 기각역보다 작게) 나오면 등분산을 만족하지 않은 상태로 진행하면 된다. 둘의 값이 다르기 때문에 이는 꼭 필요한 과정이다. -
쌍체표본 t test, paired t test
paired t test 은 '하나의 집단이 변화를 가한 후 평균이 같다' 를 확인하는 검정이다.
예시로는 'A 학교 남학생 평균 키는 약물 X 를 먹은 후에도 같다' 의 가설을 확인하기 위해 먹기 전의 키 1000개와 먹고 나서 키 1000개를 비교하는 실험이다. 약물 X 가 효과가 있는지를 확인하기 위해 하는 실험이다.
이때 paired t test 이고 같은 사람, 즉 독립적이지 않은 표본들을 가지고 하는 것이기 때문에 대응을 꼭 맞춰야 한다. 약물을 먹기 전과 후가 다른 사람이면 이 약물의 효과를 알 수 없는 것이다. 대응을 안 맞추고 진행하면 unpaired t test 나 다름없다.
ANOVA
이때 T test 은 기본적으로 2개의 집단만을 비교할 수 있다. 3개 이상의 집단에서 하나라도 평균이 다른 집단이 있는지 확인하기 위해서는 ANOVA 를 사용해야한다.
ANOVA 은 Analysis of Variance 로, F value 를 이용해 집단의 평균이 다른지를 검정하는 것이다.
ANOVA 은 크게 2가지가 있으며 one way ANOVA, two way ANOVA 이다. one way ANOVA 은 독립변수가 1개일때, two way ANOVA 은 독립변수가 2개일때 사용한다.
F test
f test 은 위에서 잠깐 서술했지만 '두 집단의 분산이 같다'를 실험하는 검정이다. 귀무가설은 '두 집단의 분산이 같다' 이며 대립가설은 '두 집단의 분산이 다르다' 이고 p value 를 통해 결정하면 된다.
