Optimizer
💡 딥러닝 분야의 학습 과정에서 반드시 사용되는 Optimizer에 대해 정리하는 시간입니다.Optimizer 종류
- Batch Gradient Descent
- Stochastic Gradient Descent
- Momentum
- Nesterov Accelerated Gradient (NAG)
- Adagrad
- RMSprop
- Adam
- Adabelief
Optimizer란?
우리가 알고 있는 딥러닝 모델의 모습은 다음과 같습니다.
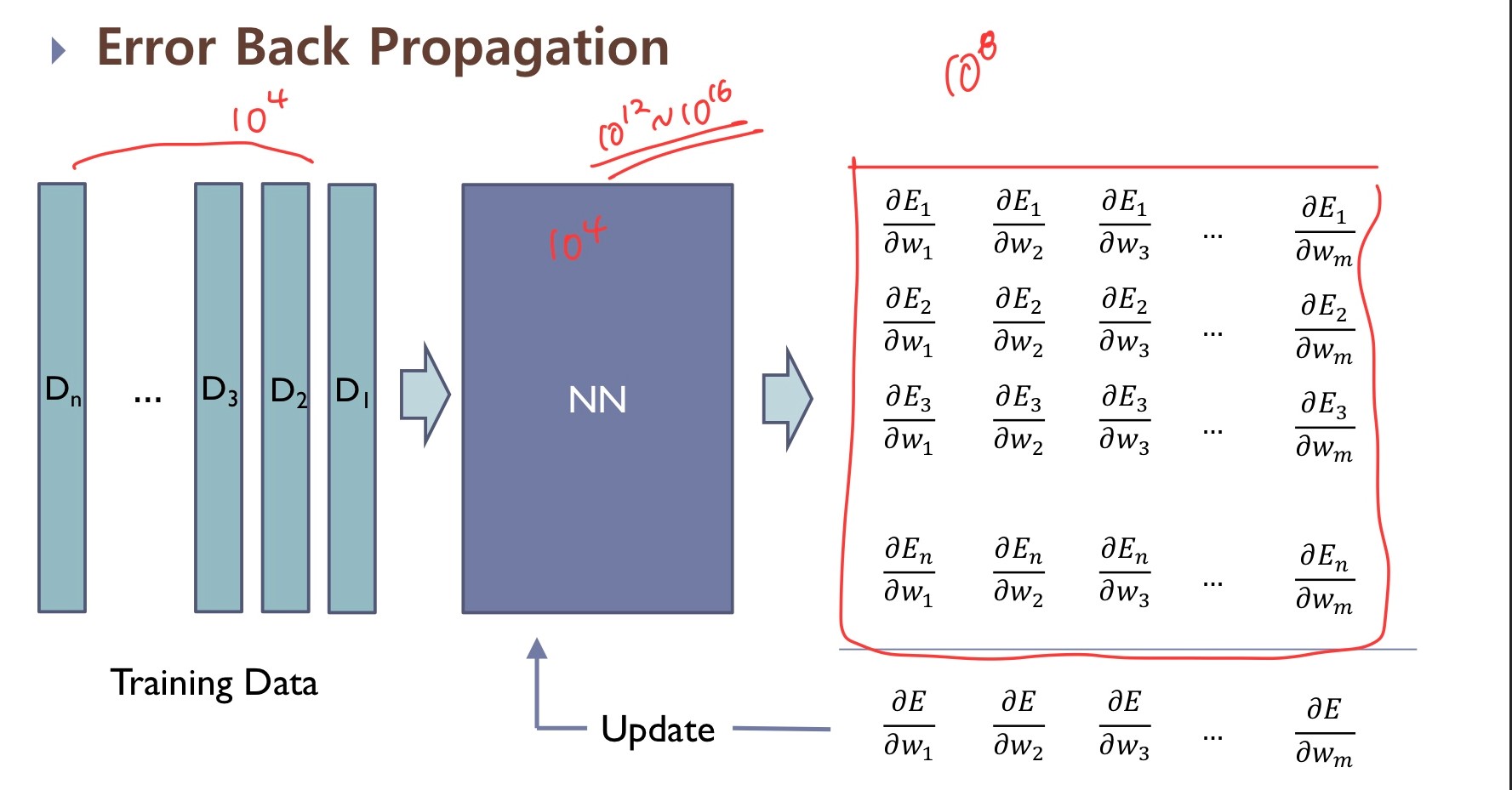
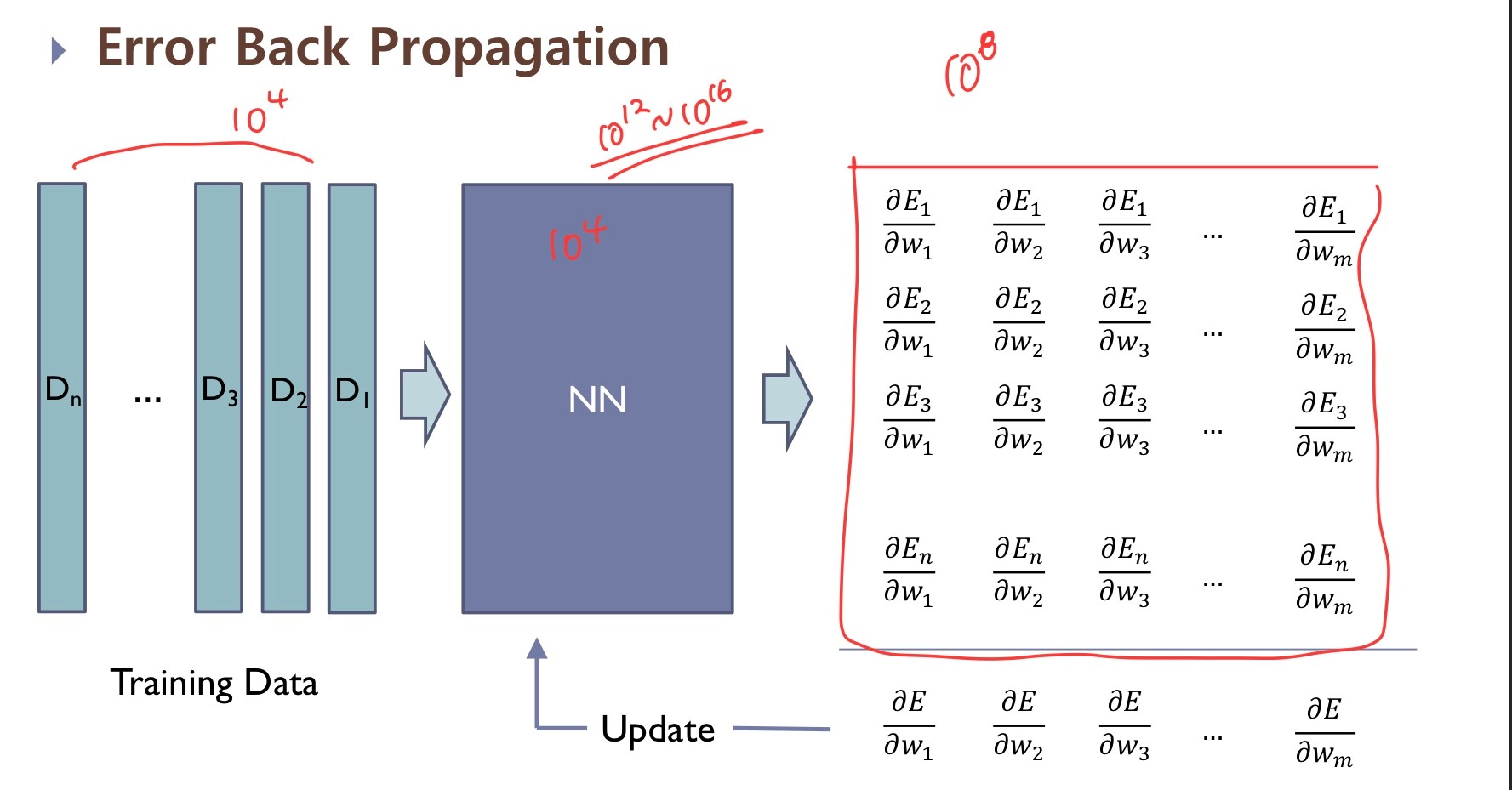
- 먼저 우리가 만든 모델에 Training Data가 들어가면 Output 값이 나옵니다.
- 우리는 그 Output값이 목표로 하는 타겟값과 가까워지도록 Error Function ( = loss function)을 설정하고 Error 값이 줄어드는 방향으로 학습시키기 위해 각 Weight와 갖는 Gradient값을 계산합니다.
- 이를 활용해 weight들을 다시 설정합니다.
- 1~3 과정을 반복(Epoch)하며 최적의 Weight를 갖는 모델을 찾아냅니다.
→ 여기서 2~4 과정을 Optimization 과정, 즉 최적화 과정이라 합니다.
< Gradient Descent (기존 Gradient Descent Method를 의미) >
Gradient Descent는 가장 기본이 되는 Optimizer 알고리즘으로 우리가 흔히 알고 있는 경사하강법입니다. GD (Gradient Descent)는 경사를 따라 내려가면서 Weight를 업데이트해, Minimum 값을 찾는 방법입니다.
- Grdient Descent 방법의 알고리즘은 다음과 같습니다.
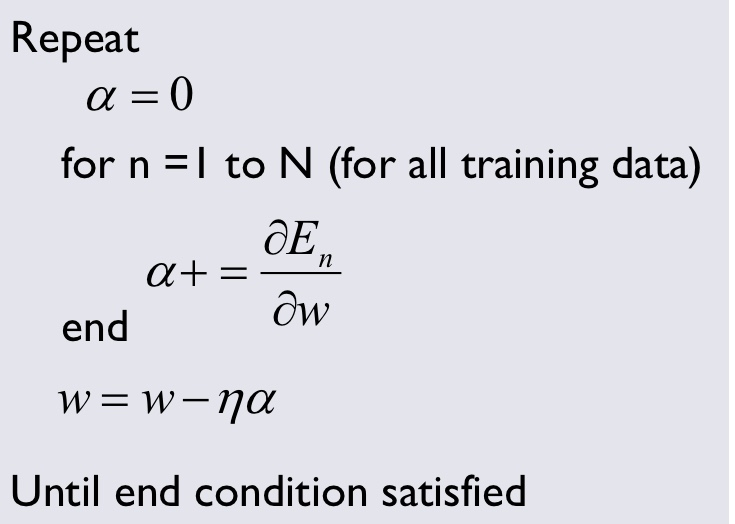
- 단점
- 모든 자료의 기울기를 다 검토하기 때문에 데이터셋의 크기가 클수록 계산량이 너무 커집니다.
- 여기서 Local minimum & Global Minimum이라는 개념이 등장하는데, 전체에서 최소가 되는 부분인 Global Minimum을 찾는 것이 Optimization의 목표인데, 이 경우 local minimum을 찾았을때 업데이트 과정이 끝난다는 단점을 가집니다. → local minimum에서 기울기 값이 0이 되니 당연하겠죠?!
<Stochastic Gradient Descent (SGD)>
-
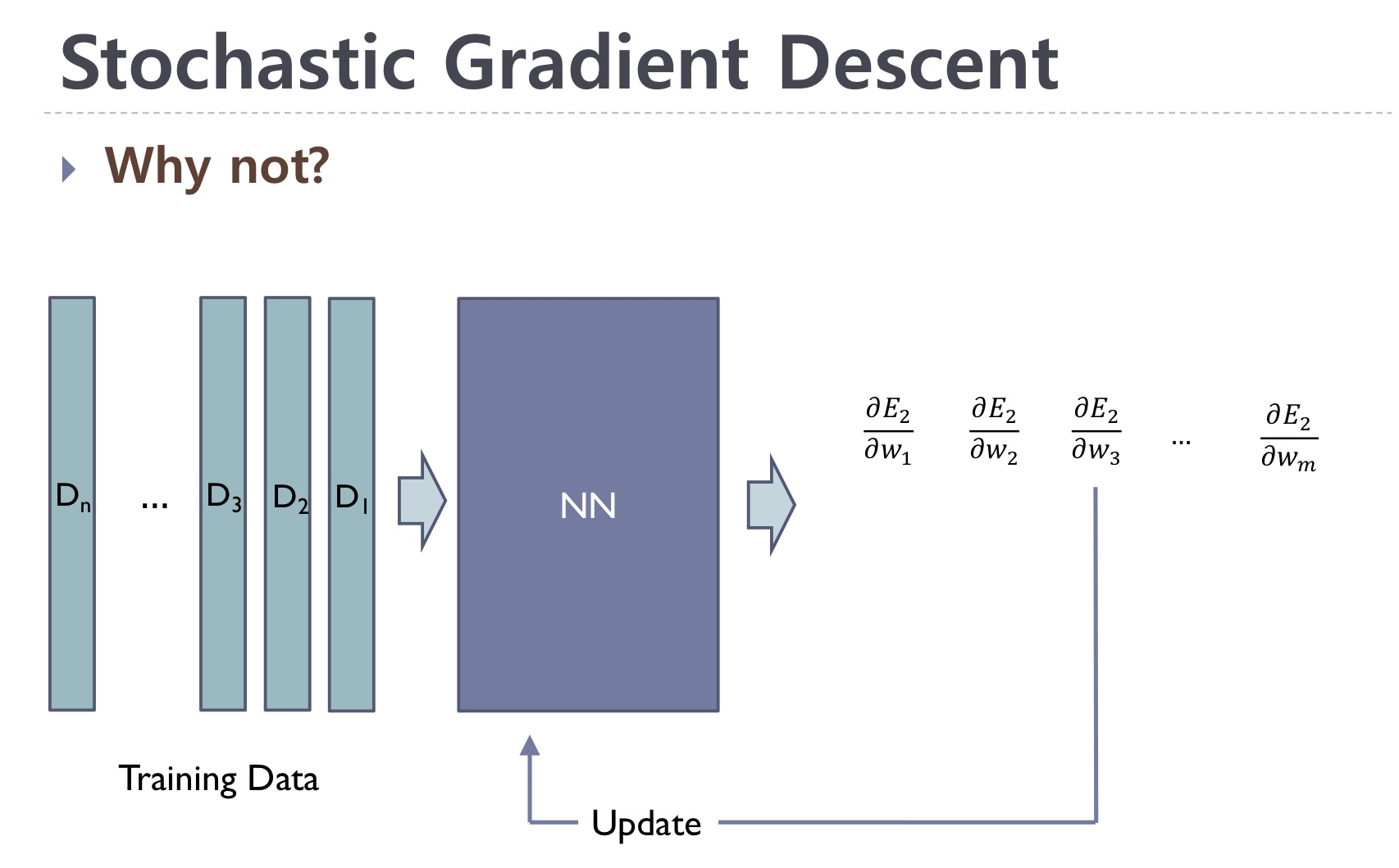
좌측의 그림은 우리가 앞에서 봤던 Gradient Descent의 과정입니다. 모든 Gradient값, 즉 기울기값을 모두 구해 합쳐 업데이트 과정을 진행하죠.
-
우측의 그림은 이제 살펴볼 Stochastic Gradient Descent (SGD)인데, 에 대해서만 Gradient를 구하고 업데이트 과정을 진행하고 있습니다. 즉, 데이터의 개수를 n개로 보았을때, 하나의 데이터당 gradient를 구해 업데이트 과정을 진행. 모든 데이터를 활용했을때는 n번의 업데이트 과정을 진행하는 것이죠.
즉, GD가 모든 기울기 값을 모두 구해 업데이트를 1회 진행한다고 한다면, SGD 방법은 하나의 데이터에 대한 기울기 값을 구해 업데이트를 진행하고 그 과정을 반복하여 총 n회 업데이트를 진행합니다.
-
Stochastic Gradient Descent 방법의 알고리즘은 다음과 같습니다.

-
GD와의 비교
- GD와 비교했을때 SGD가 동일한 시간 내에 더 좋은 성능을 보인다고 합니다. 즉, 학습속도가 좀더 빠른 것이죠.
- 하지만 두 방법 모두 Global Minimum이 아닌 Local Minimum을 찾게 된다는 단점을 갖고 있습니다.
→ 근데 결국 gradient 값을 모두 구하고 업데이트하나, 하나씩 구해 n번 업데이트하나 큰 차이가... 있을까요..?
이를 조금이나마 개선하고자 한 시도가 Mini-Batch Gradient Descent Method입니다. (조금의 방식만 추가된 것이라 자세히는 안 다룰겁니다 ㅎ) 간단히 말해서 n개의 데이터가 있다면 이를 2개씩, 3개씩 묶어서 기울기 값을 구해 업데이트하는 겁니다. n번 업데이트보다는 n/2번 업데이트하는게 시간이 좀더 적게 걸리겠죠?
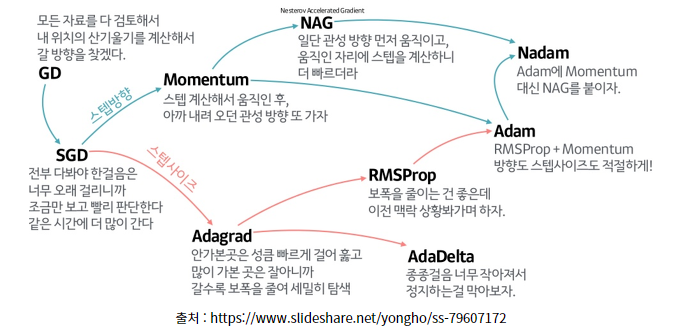
→ 앞의 방법들은 모두 Local Optimum을 구한다는 단점을 가지고 있습니다. 전체에서 가장 낮은 곳을 찾은게 아니라 어느 한 구렁텅이에 빠져서 못 나오는거에요... 이를 해결하기 위해 나온 방법이 Momentum입니다.
Momentum은 Global Optimum을 구하려면... 구렁텅이에서 빠져나오려면 어떻게 해야하지...? 라는 고민에서 시작되었습니다. Momentum이 뭘까요? 물리를 배우신 분들이라면 Momentum 모두 들어보셨을겁니다. 운동량이죠. 즉, 구렁텅이에 빠지기 전에 떨어지는 속도가 있겠죠? 이를 살려서 Local Minimum을 빠져나가보자! 라는 뜻을 가지고 있습니다.
- 그림으로 이를 비교해보면 이렇습니다.
- 그렇다면 Momentum은 어떤 단점을 가질까요? → 과도한 업데이트를 진행할 수 있습니다. Global Optimum을 찾았는데도 이게 진짜 최손가? 지금 멈추면 되니? 이럴 수 있다는 거죠.
<Nesterov Accelerated Gradient (NAG)>
Momentum 방법은 기존에 가지고 있던 Momentum, 그리고 현재 위치에서의 기울기를 고려했습니다. 근데 Momentum을 언덕을 내려가는 공으로 비유하면 눈을 감고 내려가는것과 같습니다. 이걸 좀더 똑똑하게 만들 순 없을까요? 이런 관점, 즉 언덕을 다 내려가고 다시 올라가기 전에 미리 이를 알고 속도를 줄이자! 에서 출발한 것이 NAG입니다.
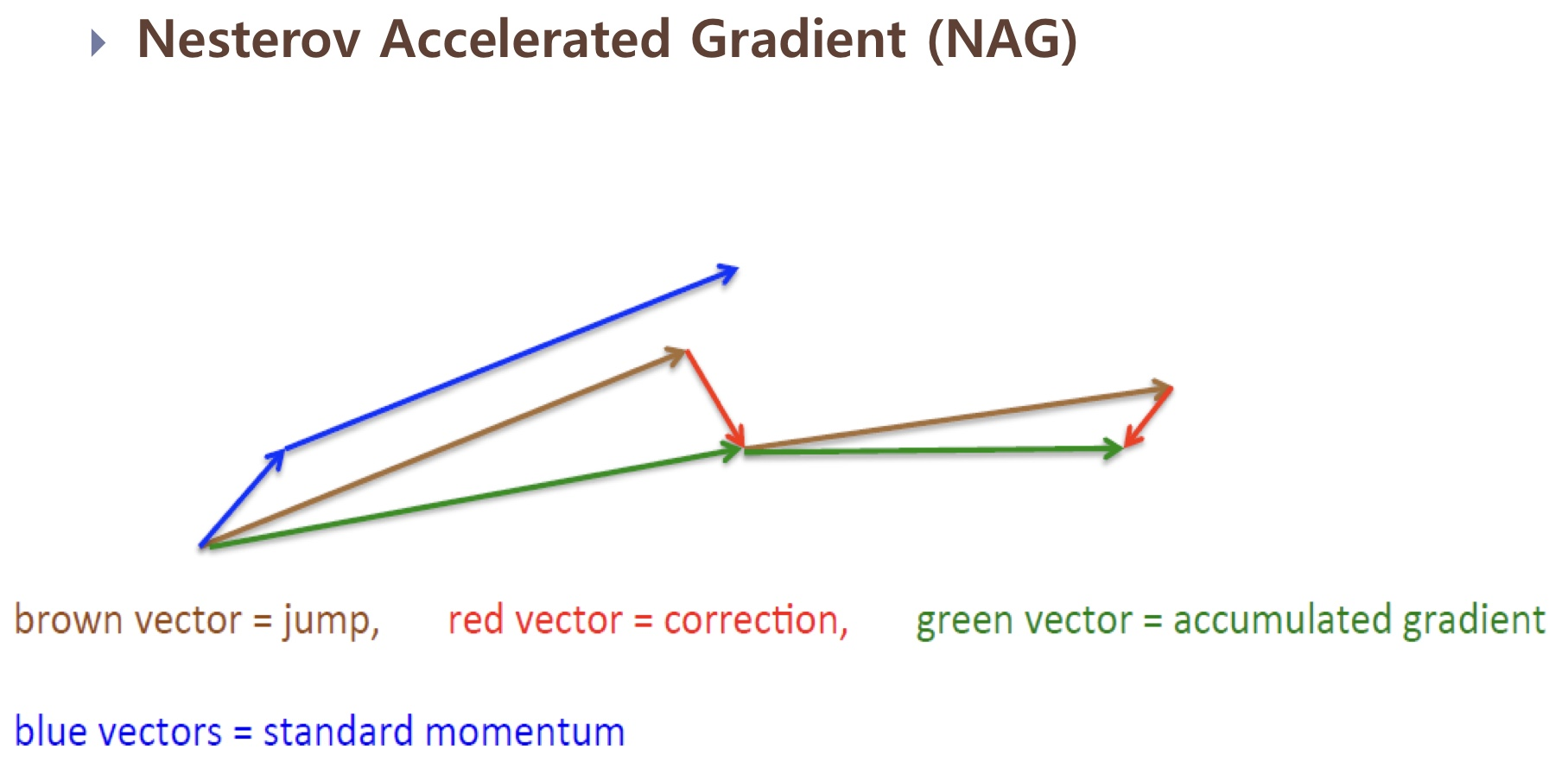
근데 그걸 어떻게... 구현할까요...? Momentum에서는 현재 위치에서 기울기를 계산했죠. NAG는 현재 위치가 아닌 미래 위치를 추정하여 거기에서 기울기를 구합니다. 즉, 1. 현재 운동량을 가졌을 때의 미래 위치를 찾는다. 2. 미래 위치에서의 기울기를 구한다. 3. 기울기를 이용해 미래 위치를 다시 계산한다.
- Momentum과 NAG를 비교하면 이렇습니다.
그런데 여기서 한 가지 의문이 생깁니다. 학습을 진행하다보면 어떤 변수는 많이 업데이트되고, 어떤 변수는 적게 업데이트되는 것을 적지 않게 볼 수 있었습니다. 우린 모든 weight에 대해 동일한 learning rate를 적용해야 할까요? 많이 업데이트된 변수는 적게, 적게 업데이트된 변수는 더 많이 업데이트할 수는 없을까요? 여기서 등장한 Optimizer가 Adagrad입니다.
Adagrad
앞에서 언급했듯이 Adagrad의 컨셉은 지금까지 비교적 훨씬 많이 업데이트된 변수는 적게, 적게 업데이트된 변순는 많이 업데이트하자! 입니다. 이를 어떻게 나타낼까요?

→ 먼저 한 변수가 지금까지 업데이트된 총량을 의 형태로 나타냈습니다. 그리고 그 변수는 루트를 씌워 분모에 위치하고 있죠. 즉, 지금까지 업데이트된 총량이 크면 분모가 커져, 업데이트하는 양은 감소합니다. 만약 총량이 작아져 분모가 작아진다면 반댈도 업데이트하는 양이 커지겠죠?
근데... 수식만 봐도 보이는 단점이 있죠? 는 시간이 지날수록 증가한다는 특징을 가집니다. 그니까 시간이 지날수록 학습률도 계속 감소하겠죠. 이런 부분을 개선하기 위해 RMSProp이 등장합니다.
RMSProp
Adagrad는 지금까지 업데이트한 전체 총량을 고려해서 업데이트를 진행했습니다. 그래서 시간이 지날수록 학습률이 계속 감소한다는 단점을 보였죠. RMSProp은 Adagrad와는 다르게 최근에 업데이트한 양을 고려합니다.
그 수식은 다음과 같습니다.

음... 수식을 보니 이렇게 표현하는게 더 좋겠네요. 지금까지 업데이트한 양과 최근에 업데이트한 양을 비교했을때 최근 업데이트한 양을 더 많이 고려하여 업데이트를 진행한다.
Adam
우리가 Optimizer에 대해서 언급할 때 많이 언급되는 Adam은 RMSProp과 Momentum의 장점을 모아 만든 Optimizer입니다.
3가지 방법을 모두 비교해보겠습니다!

- 두 방법은 공통적으로 초기 설정된 값, 값이 0으로 된다면 Weight가 초반에 0으로 정체된다는 문제점을 가집니다. 즉, 학습 초기에 값이 튀거나 불안정한 모습을 보였습니다. 이런 부분을 해결하기 위해 와 를 우측처럼 나타냈습니다. 이 부분은... 아직 완전한 이해가 되지 않아... 추가적으로 이해해보고 다시 업로드하겠습니다.
