---

이진 탐색 알고리즘 문제 중 하나인
백준 1920번 '수 찾기' 문제를 풀고 기록을 남긴다. 문제 링크

---

이진 탐색

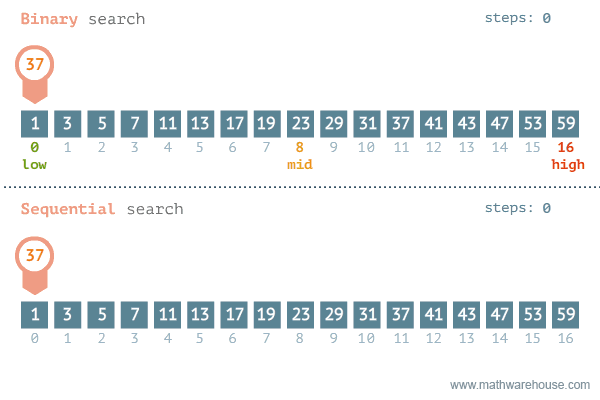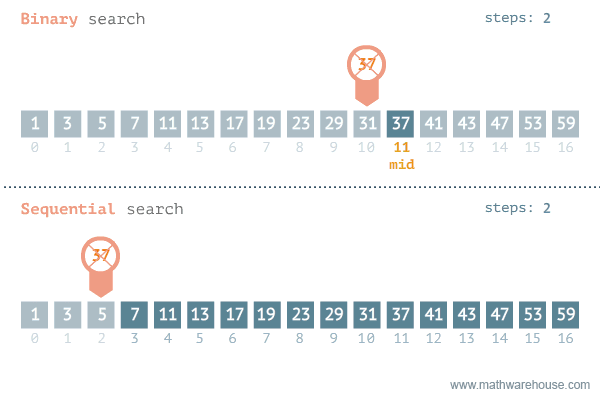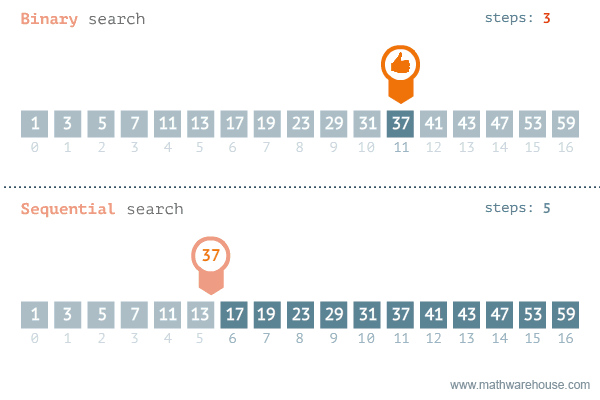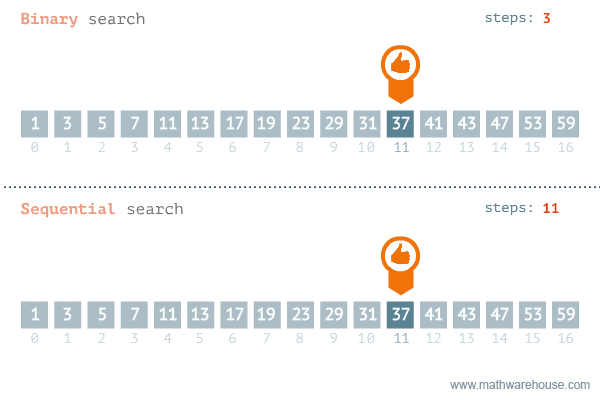
정렬된 정수의 리스트를 같은 크기의 두 부분 리스트로 나누고 필요한 부분에서만 탐색하도록 제한하여 원하는 원소를 찾는 알고리즘이다.

리스트 중간 부분에 찾는 원소가 있는지 확인하고, 없으면 위쪽에 있는지 아래쪽에 있는지 판단하여 맨 앞부터 검색하거나 중간부터 검색한다.

---

동작 방식

---

시간 복잡도

O(logN)
운이 좋다면 찾고자 하는 값이 중간값과 동일하여 탐색이 끝나지만,
최악의 경우에는 남은 데이터가 하나가 될 때 까지 반복한다.

전체 데이터 수가 N일때, 첫 번째 탐색 후 에는 N/2
두 번째 탐색에서는 N/2 1/2
세 번째 탐색에서는 N/2 1/2 * 1/2
K 번째 탐색에서는 ( 1/2 )^K × N 이 된다.

최악의 경우에는 남은 자료가 1개가 된다.

(1/2)^K x N = 1을 통해 계산하면

K = log2N 이 나온다.

---

구현 코드

def binary_search(target, data_list):
    left = 0
    right = len(data_list) - 1

    while left <= right:
        mid = (left+right) // 2
        if data_list[mid] == target:
            return mid
        elif data_list[mid] < target:
            left = mid + 1
        else:
            right = mid -1

    return -1

---

문제풀이 예시

아래는 이진 탐색을 이용해야만 시간초과 없이 풀 수 있는
백준 1920번 '수 찾기'의 정답 코드이다. 문제 링크

def binary_search(target, data_list):
    left = 0
    right = len(data_list) - 1

    while left <= right:
        mid = (left+right) // 2
        if data_list[mid] == target:
            return mid
        elif data_list[mid] < target:
            left = mid + 1
        else:
            right = mid -1

    return -1

import sys
input = sys.stdin.readline

n = int(input())
nList = list(map(int, input().split()))
nList = list(set(nList))

m = int(input())
mList = list(map(int, input().split()))

nList.sort()
for i in range(len(mList)):
    if binary_search(mList[i],nList) == -1:
        print(0)
    else:
        print(1)