DFS

DFS는 Depth-Fisrt-Search, 깊이 우선 탐색이라고 부르며, 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘입니다. DFS에서는 BFS와 마찬가지로 그래프가 사용됩니다.
이 알고리즘은 특정한 경로를 탐색하다가 특정한 상황에서 최대한 깊숙이 들어가서 노드를 방문한 후, 다시 돌아가 다른 경로로 탐색하는 알고리즘입니다.

1. DFS의 동작과정

DFS는 스택 자료구조를 이용하며 구체적인 동작 과정은 다음과 같습니다.

1. 탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다
2. 스택의 최상단 노드에 방문하지 않은 인접 노드가 있으면 그 인접 노드를 스택에 넣고 방문 처리를 합니다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼냅니다.
3. 2번의 과정을 더 이상 수행할 수 없을 때까지 반복합니다.

2. 예시

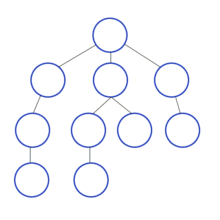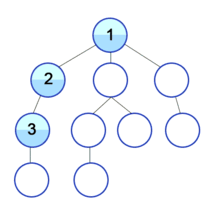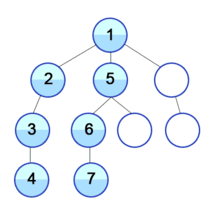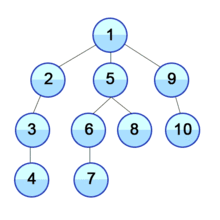
다음과 같이 스택과 그래프가 있다고 가정하겠습니다. 시작 노드를 1로 설정하고 깊이 우선 탐색을 진행하겠습니다. 이름에서 알 수 있듯이 단순하게 가장 깊숙이 위치하는 노드에 닿을 때까지 확인(탐색)하면 됩니다.

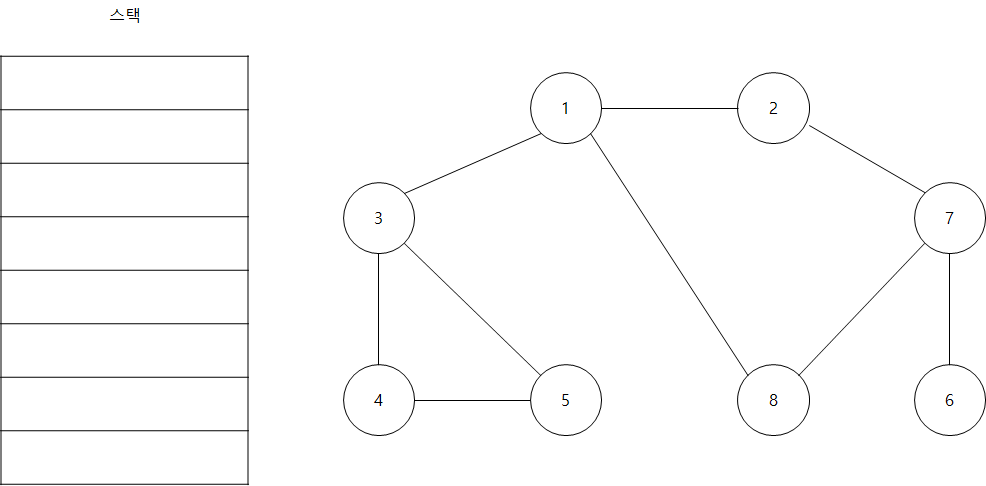
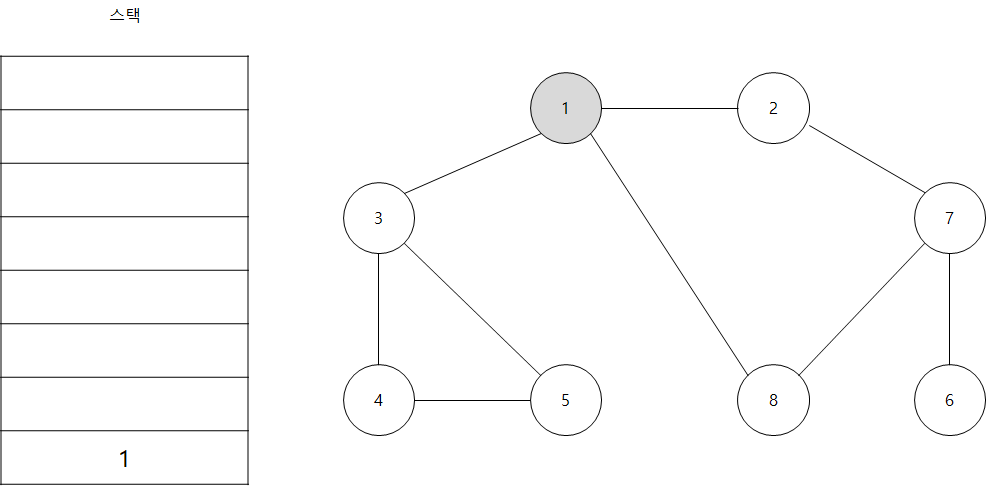
1. 시작 노드인 '1'을 스택에 삽입하고 방문 처리합니다.

처리된 노드는 회색으로, 현재 처리하는 스택의 최상단 노드는 하늘색으로 표현합니다.

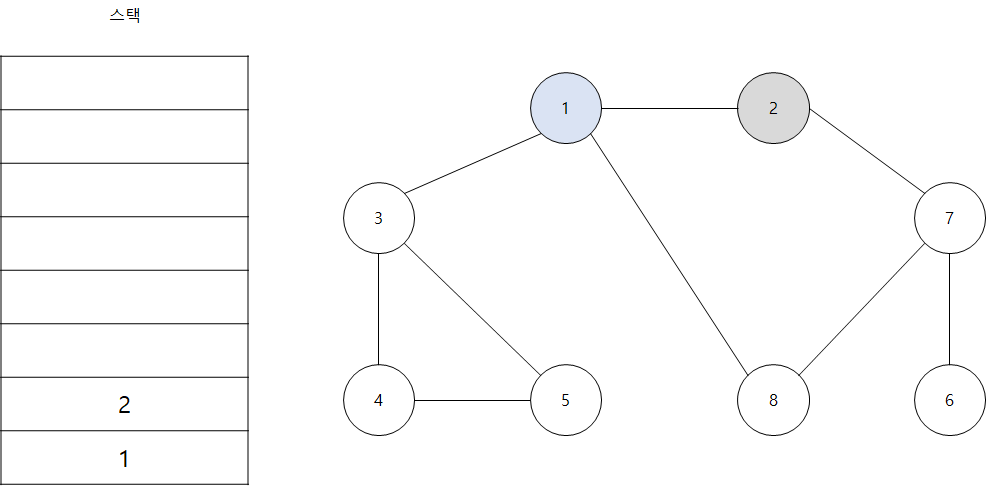
2. 스택의 최상단 노드인 '1'에 방문하지 않은 인접 노드 '2','3','8'이 있습니다. 이 중 가장 작은 노드인 '2'를 스택에 넣고 방문 처리 합니다.

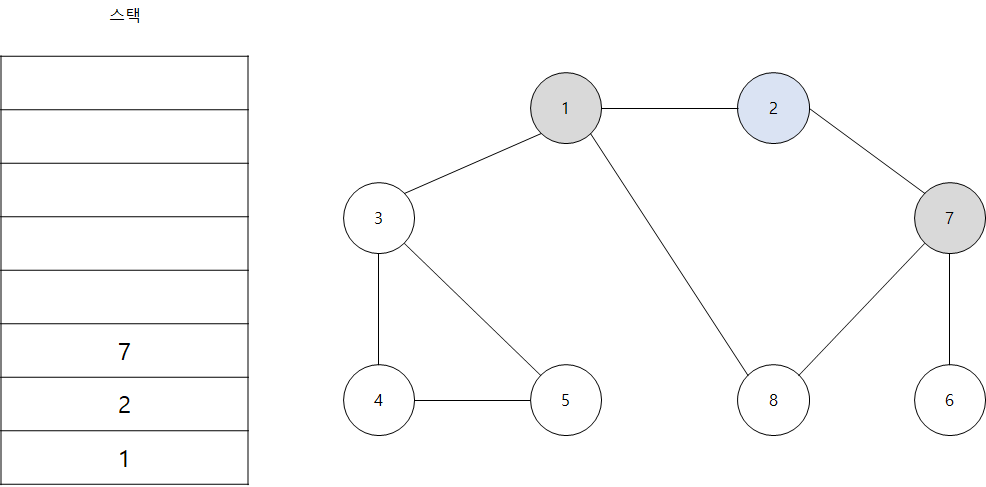
3. 스택의 최상단 노드인 '2'에 방문하지 않은 인접 노드 '7'이 있습니다. 따라서 '7'번 노드를 스택에 넣고 방문 처리를 합니다.

4. 스택의 최상단 노드인 '7'에 방문하지 않은 인접 노드 '6'과 '8'이 있습니다. 이 중에서 가장 작은 노드인 '6'을 스택에 넣고 방문 처리를 합니다.

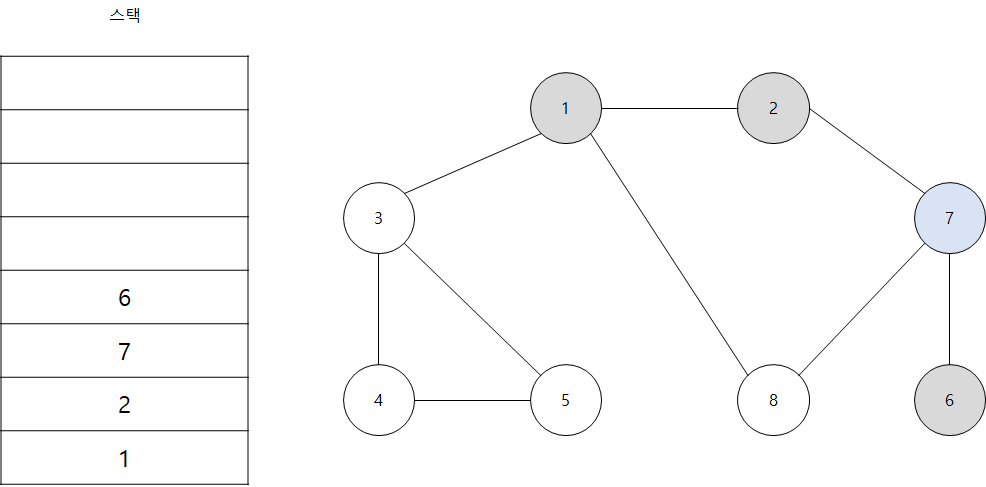
5. 스택의 최상단 노드인 '6'에 방문하지 않은 인접 노드가 없습니다. 따라서 스택에서 '6'번 노드를 꺼냅니다.

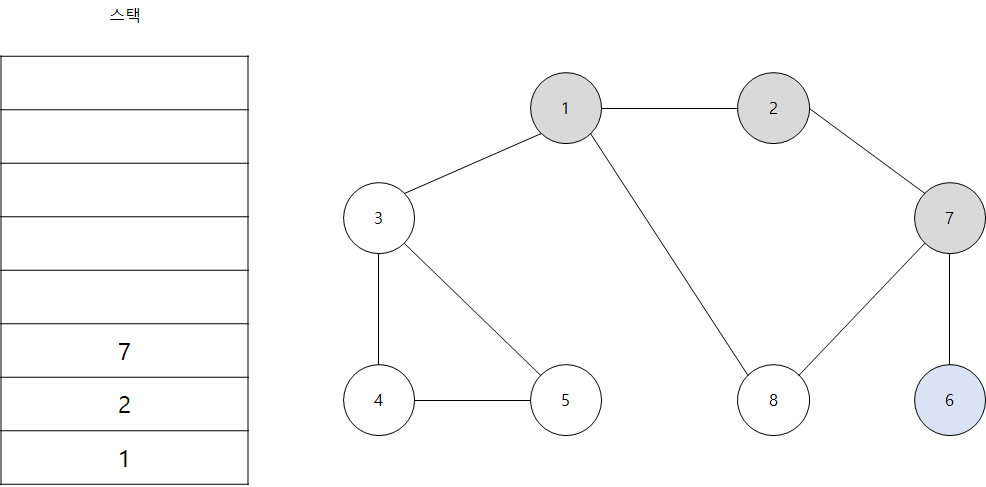
6. 스택의 최상단 노드인 '7'에 방문하지 않은 인접 노드 '8'이 있습니다. 따라서 '8'번 노드를 스택에 넣고 방문 처리를 합니다.

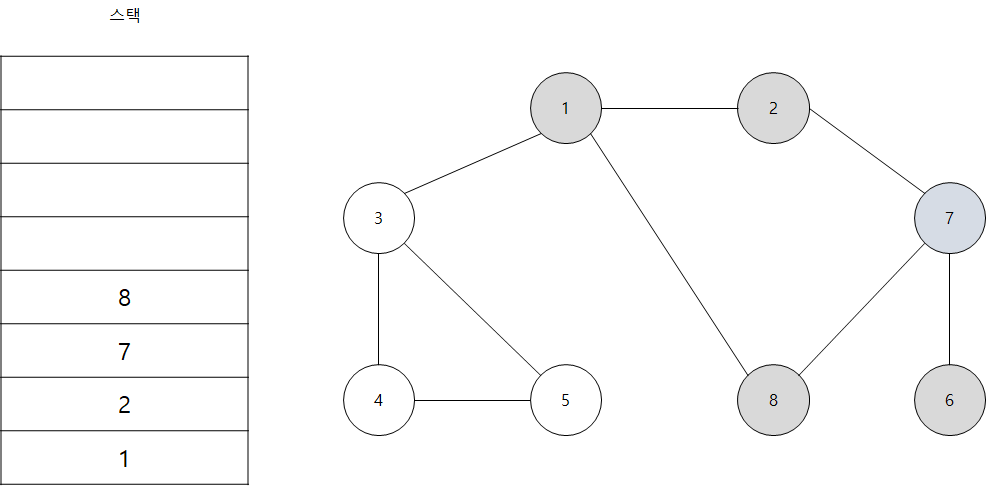
7. 스택의 최상단 노드인 '8'에 방문하지 않은 인접 노드가 없습니다. 따라서 스택에서 8번 노드를 꺼냅니다. 이렇게 8번 노드, 7번 노드, 2번 노드가 더 방문 할 인접 노드가 없으므로 모두 스택에서 꺼냅니다.

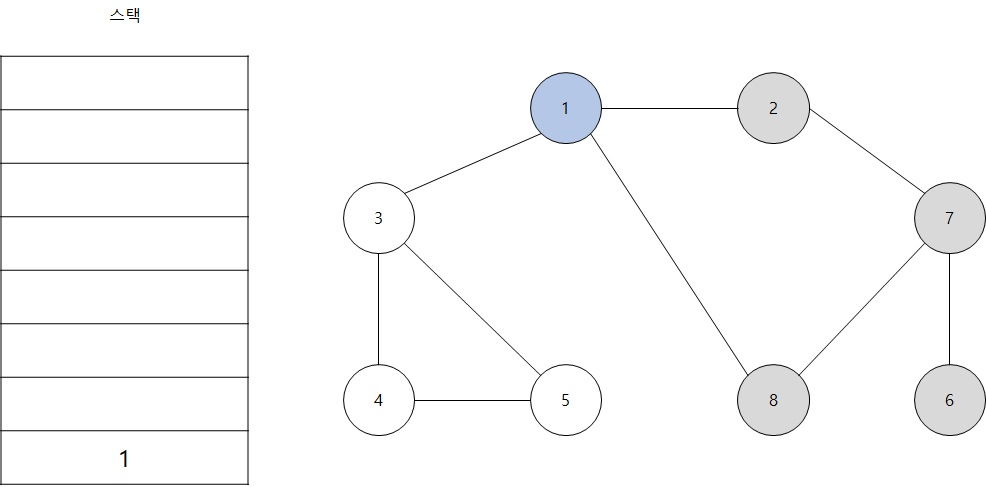
8. 스택의 최상단 노드인 '1'에 방문하지 않은 인접 노드 '3'을 스택에 넣고 방문 처리합니다.

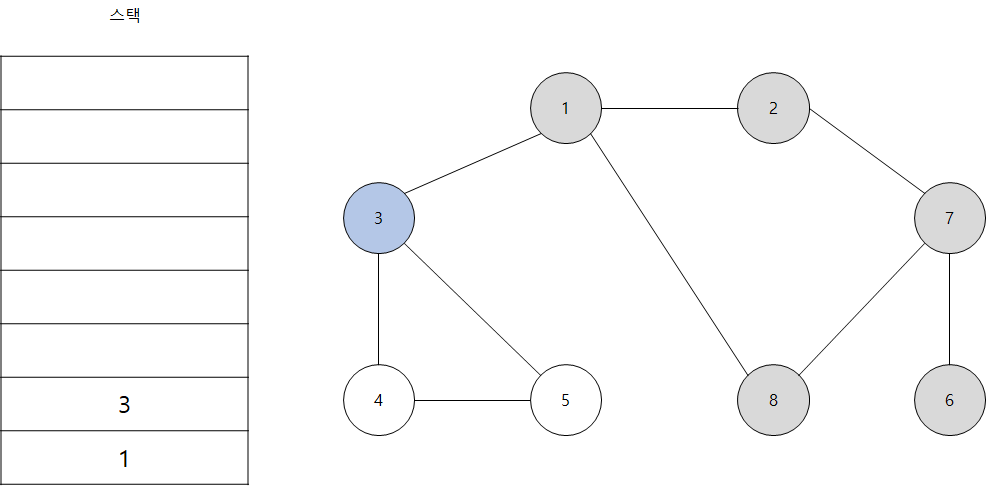
9. 스택의 최상단 노드인 '3'에 방문하지 않은 인접 노드 '4'와 '5'가 있습니다. 이 중에서 가장 작은 노드인 '4'를 스택에 넣고 방문 처리를 합니다.

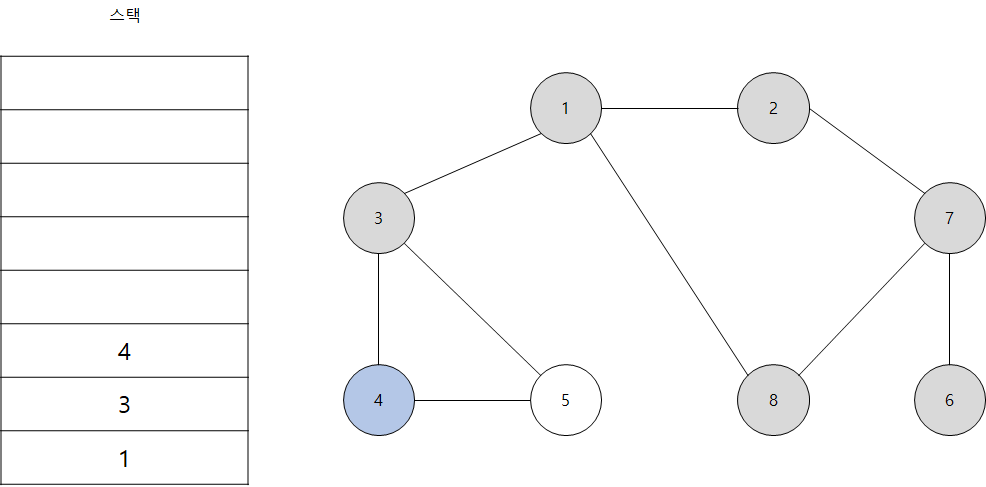
10. 스택의 최상단 노드인 '4'에 방문하지 않은 인접 노드 '5'가 있습니다. 따라서 '5'번 노드를 스택에 넣고 방문 처리를 합니다.

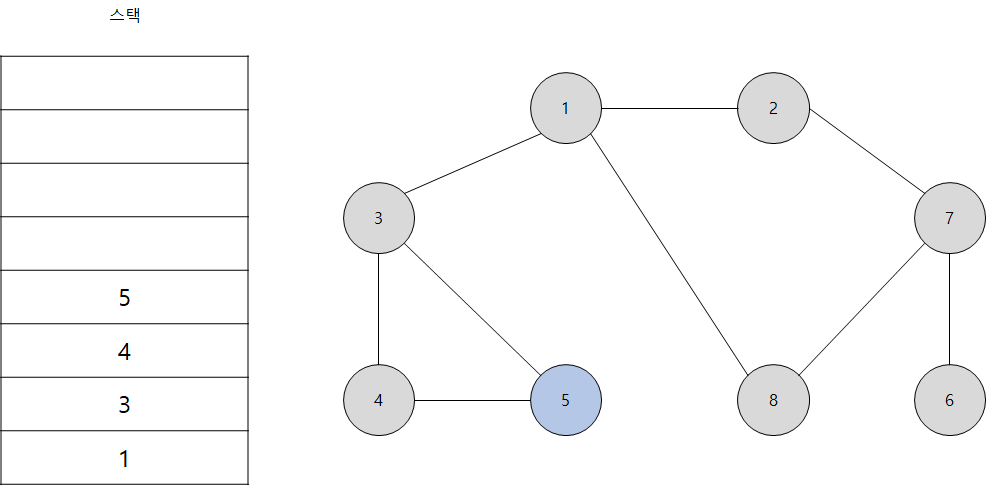
11. 이제 스택의 최상단 노드부터 방문하지 않은 인접 노드를 확인하는데 모두 방문하였으므로 스택에서 꺼내주면 됩니다.

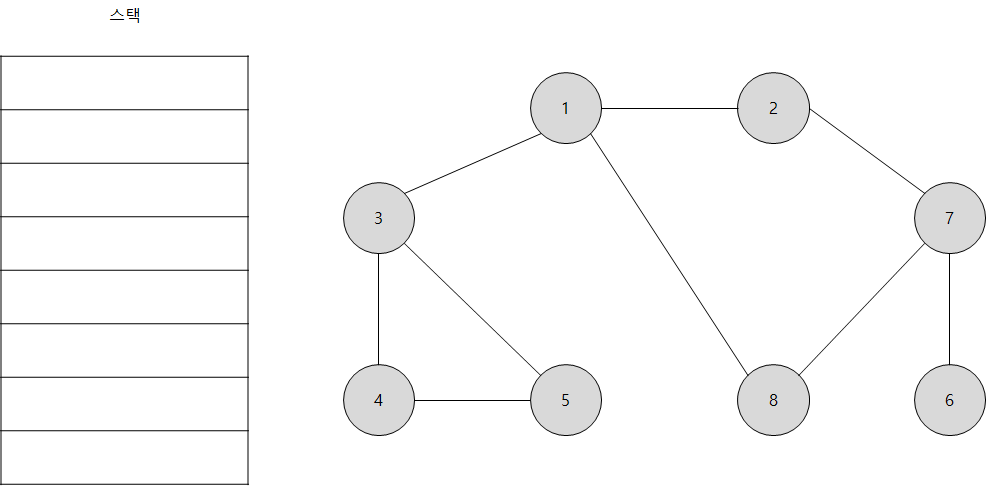
결과적으로 탐색의 순서(스택에 들어간 순서)는 1 -> 2 -> 7 -> 6 -> 8 -> 3 -> 4 -> 5 입니다.
깊이 우선 탐색 알고리즘인 DFS는 스택 자료구조에 기초합니다.
실제로는 스택을 쓰지 않고 재귀 함수로 구현할 수 있으며 탐색을 수행함에 있어서 데이터의 개수가 N개인 경우 O(N)의 시간이 소요됩니다.

3. 코드

재귀를 이용한 코드 - 1

# DFS 메서드 정의
def dfs(graph, v, visited):
    # 현재 노드를 방문 처리
    visited[v] = True
    print(v, end=" ")
    # 현재 노드와 연결된 다른 노드를 재귀적으로 방문
    for i in graph[v]:
        # 해당노드가 만약 방문하지 않았다면
        if not visited[i]:
            # 재귀적으로 메서드 호출
            dfs(graph, i, visited)

# 각 노드가 연결된 정보를 리스트 자료형으로 표현(2차원 리스트)
graph = [
    [],
    [2,3,8],
    [1,7],
    [1,4,5],
    [3,5],
    [3,4],
    [7],
    [2,6,8],
    [1,7]
]

# 각 노드가 방문된 정보를 리스트 자료형으로 표현
visited = [False] * 9

# 정의된 DFS 함소 호출
# 2차원 리스트, 시작 노드, 방문 처리 리스트
dfs(graph, 1, visited)

결과는 1 2 7 6 8 3 4 5 가 출력됩니다.

재귀를 이용한 코드 - 2(깔끔하게)

def recursive_dfs(v, discovered=[]):
    discovered.append(v)
    for w in graph[v]:
        # 방문한적이 없다면
        if w not in discovered:
            # 연결된 노드 재귀 호출
            discovered = recursive_dfs(w, discovered)

    return discovered

스택을 이용한 구현

def iterative_dfs(start_v):
    # 결과 변수
    discovered = []
    # 리스트 선언(스택)
    stack = [start_v]
    # 스택이 비어있지 않는 동안에
    while stack:
        v = stack.pop()
        # 방문한적이 없다면
        if v not in discovered:
            discovered.append(v)
            for w in graph[v]:
                stack.append(w)

    return discovered

4. 정리

다양한 방식으로 구현할 수 있지만 아래의 표와 같이 구현하는 것이 가장 간결한 방식입니다.

	DFS	BFS
동작원리	스택	큐
구현방법	재귀 함수 이용	큐 자로구조 이용

참조
취업을 위한 코딩 테스트다 with 파이썬
위키백과 - 깊이 우선 탐색

틀린 부분은 댓글로 남겨주시면 수정하겠습니다..!!