구간 합 계산
구간 합 문제란 연속적으로 나열된 N개의 수가 있을 때, 특정 구간의 모든 수를 합한 값을 구하는 문제를 말합니다. 예를 들어 5개의 데이터로 구성된 수열 {10, 20, 30, 40, 50}이 있다고 가정하겠습니다. 여기에서 두 번째 수부터 네 번째 수까지의 합은 20 + 30 + 40으로 90이 될 것 입니다.
이러한 구간 합 계산 문제는 여러 개의 쿼리로 구성되는 문제 형태로 출제되는 경우가 많습니다. 다수의 구간에 대해서 합을 각각 구하도록 요구됩니다. 예를 들어 M개의 쿼리가 존재한다고 가정하면 각 쿼리는 Left와 Right로 구성되며, 이는 [Left, Right]의 구간을 의미합니다. 결과적으로 M개의 쿼리가 주어졌을 때, 모든 쿼리에 대하여 구간의 합을 출력하는 문제가 전형적인 '구간 합 계산' 문제입니다.
만약 M개의 쿼리에 대해 각각, 매번 구간 합을 계산한다면 이 알고리즘은 O(NM)의 시간복잡도를 가집니다. 왜냐하면, M개의 쿼리가 수행될 때마다 전체 리스트의 구간 합을 모두 계산하라고 요구(첫 번째 부터 N번째 수까지)할 수도 있기 때문입니다. 결과적으로 O(NM)의 시간 복잡도를 가지는데, 이는 데이터의 개수가 매우 많을 때 해당 복잡도로는 문제를 해결할 수 없습니다.
항상 우리가 알고리즘을 설계할 때 고려해야 할 점은, 여러 번 사용될 만한 정보는 미리 구해 저장해 놓을수록 유리하다는 것입니다. 확인해보면 쿼리는 M개이지만 N개의 수는 한 번 주어진 뒤에 변경되지 않습니다. 따라서 N개의 수에 대해서 어떠한 '처리'를 수행한 뒤에 나중에 M개의 쿼리가 각각 주어질 때마다 빠르게 구간 합을 도출하면 됩니다.
구간 합 계산을 위해 가장 많이 사용되는 기법이 접두사 합(Prefix Sum)입니다. 각 쿼리에 대해 구간 합을 빠르게 계산하기 위해서는 N개의 수의 위치 각각에 대하여 접두사 합을 미리 구해 놓으면 됩니다. 여기서 접두사 합이란 리스트의 맨 앞부터 특정 위치까지의 합을 구해 놓은 것을 의미합니다.
구간 합을 빠르게 계산하는 알고리즘
- N개의 수에 대하여 접두사 합(Prefix Sum)을 계산하여 배열 P에 저장합니다.
- 매 M개의 쿼리 정보[L, R]을 확인할 때, 구간 합은 P[R] - P[L-1]입니다.
예를 들어 다음과 같이 5개의 데이터가 있다고 가정하겠습니다.

이 5개의 데이터에 대해서 접두사 합을 계산하면 다음과 같습니다.
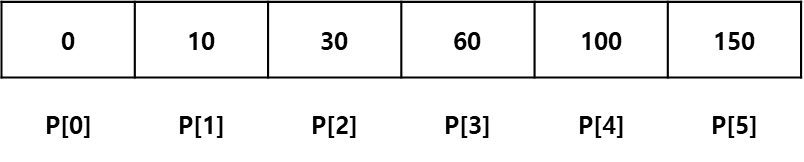
위에서 설명한 알고리즘대로 매 쿼리가 들어왔을 때, P[R] - P[L-1]을 계산하면 바로 구간 합을 구할 수 있게 됩니다. 따라서 매 쿼리당 계산 시간은 O(1)이 됩니다. 결과적으로 N개의 데이터와 M개의 쿼리가 있을 때, 전체 구간 합을 모두 계산하는 작업은 O(N + M)의 시간복잡도를 가집니다.
구하는 과정
만약 다음과 같이 쿼리 3개가 있다고 가정했을 때, 구간 합을 구하는 과정은 아래와 같습니다.
1. 첫 번째 쿼리는 첫 번째 수부터 세 번째 수까지의 구간 합을 물어보는 [1,3]이라고 하겠습니다. 이 경우, P[3] - P[0] = 60이 답이 됩니다.
2. 두 번째 쿼리는 두 번째 수부터 다섯 번째 수까지의 구간 합을 물어보는 [2,5]라고 하겠습니다. 이 경우, P[5] - P[1] = 140이 답이 됩니다.
3. 세 번째 쿼리는 세 번째 수부터 네 번째 수까지의 구간 합을 물어보는 [3,4]라고 하겠습니다. 이 경우, P[4] - P[2] = 70이 답이됩니다.
소스코드
# 데이터의 개수 N과 전체 데이터 선언
n = 5
data = [10, 20, 30, 40, 50]
# 접두사 합(Prefix Sum) 배열 계산
sum_value = 0
prefix_sum = [0]
for i in data:
sum_value += i
prefix_sum.append(sum_value)
# 구간 합 계산(세 번째부터 네 번째 수까지)
left = 3
right = 4
print(prefix_sum[right] - prefix_sum[left - 1])