📌PINN에 대해 이해하기
📕 딥러닝 단점
딥러닝
- 데이터기반접근의 이점이있다.
- 데이터가 꽤 많으면 적당한 모델에 적당한 성능가능
- 더 ~ 좋은성능? 은 데이터만으로 한계가있다.
블랙박스단점
1. interpretability X = 해석 불가
2. generalizability X = 일반화 불가
- 내삽은되는데 외삽은..?
위를 극복하기위해서는?
- 데이터 품질개선
- 알고리즘 개선
- 주제 : Physics 를 적용하자!
📕 딥러닝과 Physics의 조합
왜 데이터기반의 블랙박스 방법이 실패할까?
- 아마 추론값은 물리적 정합성이 떨어질것이다.
- 그럴듯하게 보이는건, 사용데이터가 시뮬레이션결과값이기때문
딥러닝과 Pysics를 결합하면?
- 데이터와 상관없이 우리가 정확히 하는 물리적법칙은 꼭 맞추게끔 학습한다면 물리법칙관련 딥러닝에서는 성능이 우수하지않을까?
만약 데이터가 일렬로 네개의 점이 주어져있다면?
- 데이터만을가지고 회귀를 한다면 네점을 잇는 직선이 회귀선이 될 수 있다.
- 하지만 알고봤더니 네개의 점은 어떠한 함수식에서 샘플링된 값이 었던것
- 그래서 예측한 회귀선은 실제 함수식과 달랐다.
- 만약 기존 함수식을 안다면?
- 데이터 뿐만 아니라 함수식까지 맞추도록 학습한다면 정확한 회귀선을 구할 수 있었을 것
📕 딥러닝으로 미분방정식 풀이
가정 : 주어지는 데이터가없음
ANN은 Universal approximators 이다.
- 어떠한 함수도 근사할수있다!
정리필요한내용들
상미분방정식(ODE)
선형방정식
비선형방정식
편미분방정식(PDE)나중에볼 논문
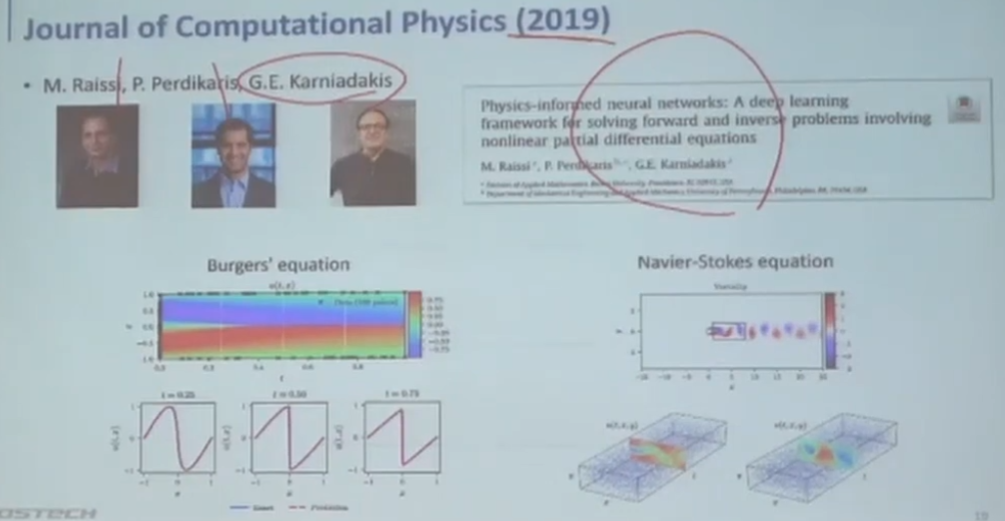
ANN을 가지고 PDE가 있을때 Regulaization을 통해 Physics를 집어넣겠다.
📖 모델설명

만약 ANN의 입력이 x,t이고 출력이 u일떄
ANN은 어느정도 함수를 근사할 수 있다했으니, 해당 입력값에 대한 어느정도의 함수를 근사했을것.
편미분방정식을 알고있다면, 출력u에 대해 편미분방정식을 구해 비교하여 해당 Loss를 줄이는 방향으로 ANN의 가중치를 업데이트한다.
- BC : 경계조건
- IC : 초기조건
📖 모델특징
- 데이터가 필요없다.
- loss function에 multiple term 이 들어간다.
- adam과 quasi-newton L-BFGS optimizers가 사용된다.
- 메시가 없다. (대신 4번이필요)
- Deep collocation method를 사용한다.
- 빨간색 원 : collocation point
- 좌측 파란색 X : initial condition
- 위/아래 파란색 X : Boundary condition
- monte carlo sampling method

실습내용보면,
- 쌩으로 코딩할건지
- 라이브러리를 사용할건지
두가지로 나와있다.
PINN논문 저자중 한명이 교수가 됐는데 그 사람이 PINN을 편리하게 사용하기 위한 라이브러리를 만들었음.
📕 Physics + data
📕 한계점과 발전가능성
📖 한계점
discontinue 한 상황에 수렴이되지 않는다.
- CAE 에서 발생했던 문제점과 동일하다.
- 제안하는 해결점도 CAE에서와 동일
1. Weak form PDE- Domain decomposition
- 용어가 어렵네...
- 뭐라는거지?
📖 발전가능성
기존 CAE 해석은 공간을 그리드로 분할하고
그리드간의 차분? 연산을 통해 해석을 수행함 즉 LOCAL이다.
하지만 PINN에서 사용하는 모델은 ANN 으로 1차원벡터로 만들어서 입력으로 넣기때문에 GLOBAL하다.
이러한 문제점을 해결하기 위해 CNN같은 계열이 들어와야하나,
CNN은 랜덤한 위치가 아닌 격자형태로 이루어진 배열을 입력으로 받으므로 PINN의 데이터를 사용할수없다.
따라서 Graph NN 을 사용한 연구가 진행되고있다.
--> PIGNN
📚 Reference
해당 내용들은 전~부 아래 링크의 내용을 가져왔습니다.
설명 너무잘하셔서 이해 쏙쏙됩니다 관심있으시면 한번 보세요