부스트 캠프 AI Tech 3일차

오늘 새로 알게된 내용

- 신경망 모델

• 기본적으로 비선형 모델
• 선형 모델과 비선형 함수로 이루어진 모델
• 동작 방식과 비선형 학습 패턴에 대한 이해가 필요
  
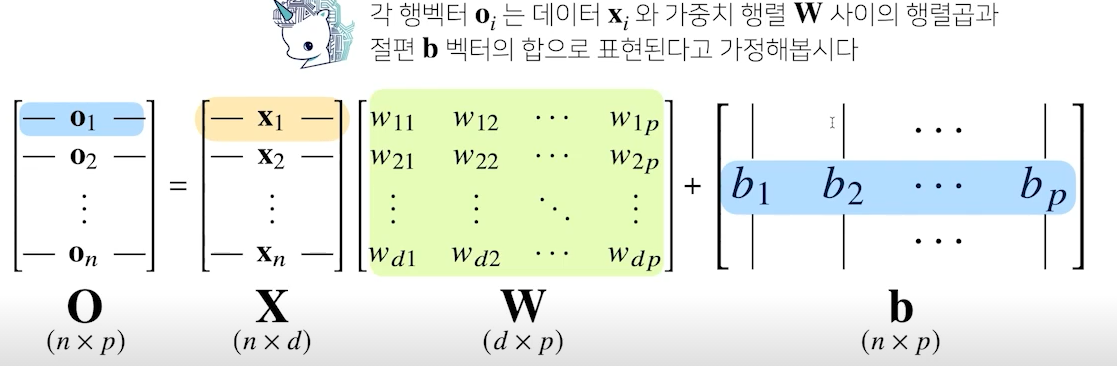
• X : 전체 데이터가 모여있는 행렬, 각 행데이터는 각 데이터 포인트
• W : 가중치 행렬 W, 다른 데이터 공간으로 변환해주는 역할
• b : y절편 벡터들의 행렬 $b1, bp$ 까지 모든 행에 대해서 동일한 값 적용
• O : 출력 데이터 행렬, 입력 데이터의 입력 데이터 형태와 가중치 데이터 형태에 따라 출력 데이터의 형태가 달라짐
  - d개의 입력 변수를 p개의 선형 모델을 만들어서 p개의 잠재 변수 생성
  
  

- softmax

• 소프트맥스 함수는 모델의 출력을 확률로 해석할 수 있게 변환해 주는 연산
• 분류 문제를 풀 때 소프트맥스 함수를 결합하여 예측
  
• 소프트맥스(softmax)함수는 모델의 출력을 확률로 해석할 수 있게 변환해주는 연산
• 분류 문제를 풀 때 선형모델과 소프트맥스 함수를 결합하여 예측
• activation function 중 하나로, 이진분류 이상의 결과를 해석할 떄 사용
  
  

- 신경망

• 신경망은 선형 모델과 활성화 함수를 합성한 함수
  
  

- Multi-layer perceptron

MLP는 신경망이 여러 층으로 합성된 함수

• H는 Z에 활성화 함수를 적용한 값
• 이 층을 여러 개 쌓은 형태(MLP)
• Z를 출력하는 선형회귀식에서 weight와 bias는 층 개수만큼 행렬의 형태로 생성됨
• 입력부터 출력까지 순차적으로 신경망을 계산하는 것을 순전파(forward propagration)이라 한다

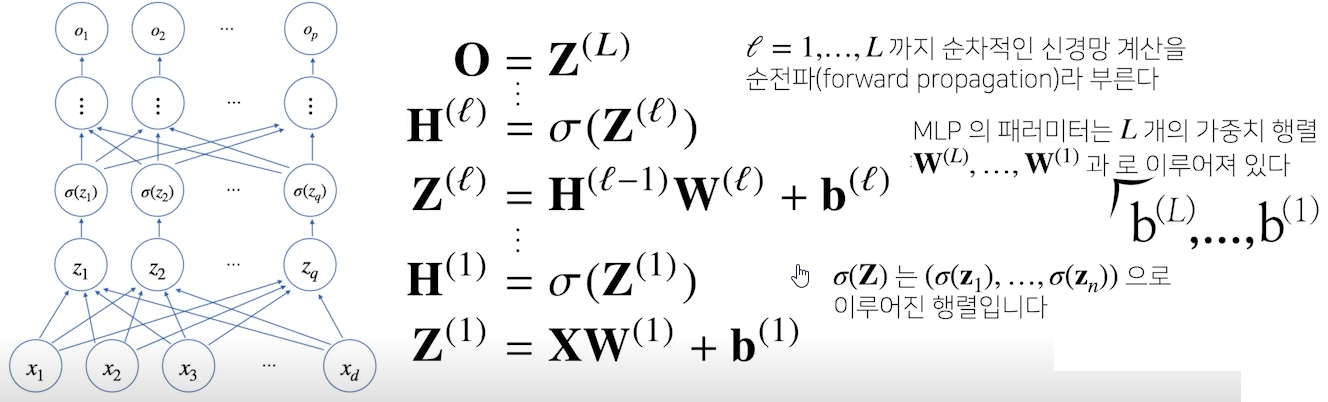
층을 여러개 쌓는 이유

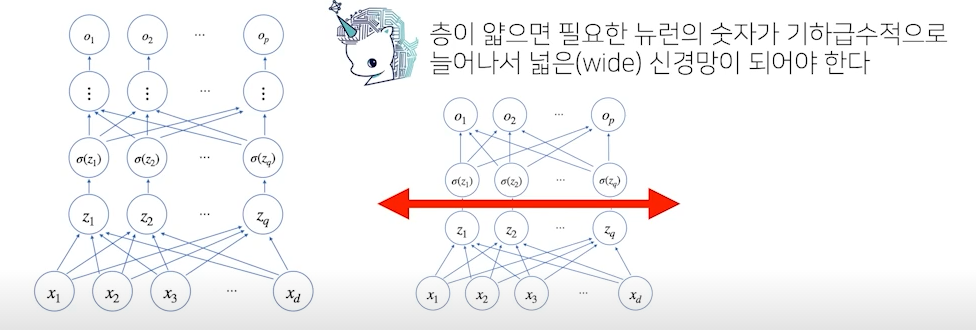
• 이론적으론 2층 신경망으로도 임의의 연속함수를 근사 가능
• 단 층이 깊을 수록 목적 함수를 근사하는데 필요한 뉴런(노드)의 개수가 훨씬 빨리 줄어들어 좀 더 효율적으로 학습이 가능
  - 적은 뉴런의 개수로 조금 더 빠르게 목적함수로 근사 가능
  - 층이 깊어질수록 적은 파라미터로도 복잡한 함수를 표현 가능
• 복잡한 패턴의 데이터일 경우 조금 더 깊은 신경망을 통해 목적 함수로 근사 가능
• 단, 층이 깊다고 복잡한 함수로 근사를 할 수 있지만, 최적화가 어려워질 수 있음(학습)
  

고민한 내용 및 결과

회고

작심삼일이 중요하다