🔎 이진 탐색 트리란?
- 이진 검색 트리는 연결된 노드(노드에 저장된 데이터)들을 가지고 있는 트리 구조입니다.
- 각 노드에는 최대 두 개의 자식 노드가 있으며, 왼쪽 자식 노드는 현재 노드보다 작은 값을 가지고 있고, 오른쪽 자식 노드는 현재 노드보다 큰 값을 가지고 있습니다.
이진 탐색 트리의 특징
- 왼쪽 자식은 현재 노드보다 작은 값을 가지고 있으며,
오른쪽 자식은 현재 노드보다 큰 값을 가집니다. - 중복된 값은 허용되지 않습니다.
- 각 노드의 왼쪽 서브트리에 있는 모든 값은 현재 노드보다 작고,
오른쪽 서브트리에 있는 모든 값은 현재 노드보다 큽니다.
- 모든 리프 노드는 None으로 표시됩니다.
그냥 왼쪽 왕작다 오른쪽 왕크다로 생각해요.

21이 루트 노드이고, 다음으로 28을 트리에 삽입할 때 21보다 큰 값이므로 오른쪽으로 간다.
그 다음 값인 14는 21보다 작으므로 왼쪽으로 간다.
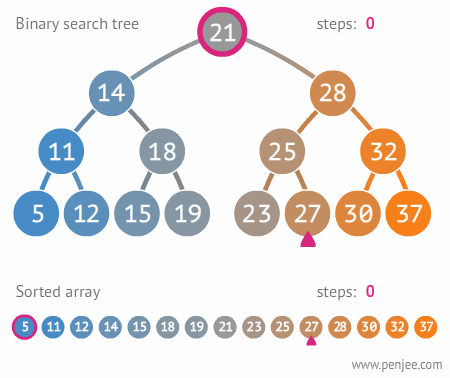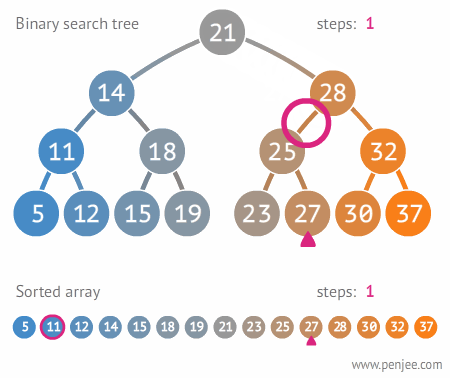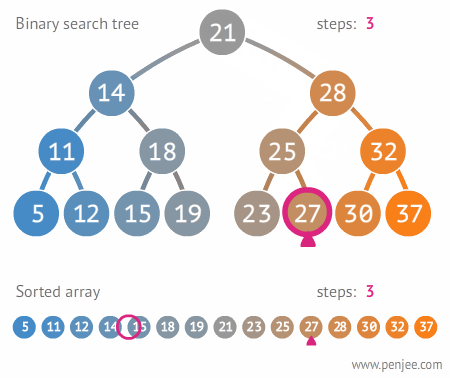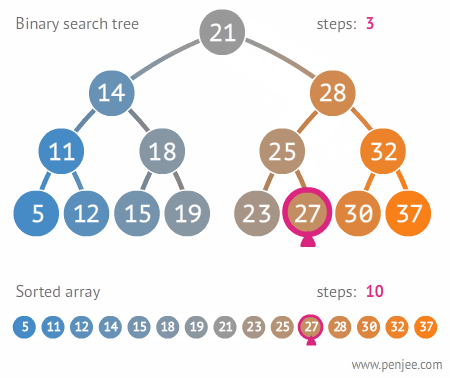
이진 탐색 트리 구현
class Node:
def __init__(self,data):
self.data = data
self.left = None
self.right = None
class BinarySearchTree:
def __init__(self):
self.root = None- 각 노드를 나타내는 클래스를 정의합니다
- 각 노드의 데이터와 왼쪽, 오른쪽 자식 노드를 저장하는 Node클래스를 정의한 것입니다.
- BinarySearchTree 클래스는 이진 탐색 트리를 나타내고, root 변수를 통해 트리의 루트 노드를 가리킵니다.
삽입(Insert)
def insert(self,data):
if self.root is None:
self.root = Node(data)
else:
self._insert_recursive(self.root,data)
def _insert_recursive(self, root, data):
if data < root.data:
if root.left is None:
root.left = Node(data)
else:
self._insert_recursive(root.left,data)
elif data> root.data:
if root.right is None:
root.right = Node(data)
else:
self._insert_recursive(root.right,data)- insert(self, data)
- 이 메서드는 새로운 데이터(data)를 BST에 삽입하는 역할을 합니다.
- 먼저, 트리가 비어있으면(root가 None인 경우) 새로운 노드를 생성하여 루트로 설정합니다.
- 비어 있지 않으면
_insert_recursive메서드를 호출하여 재귀적으로 삽입을 수행합니다.
- _insert_recursive(self,root,data)
- 이 메서드는 실제로 데이터를 삽입하는 재귀적인 방식을 구현합니다
- root는 현재 서브트리의 루트 노드를 가리키며, data는 삽입할 값입니다.
- 삽입할 데이터(data)가 현재 노드의 데이터보다 작으면
왼쪽서브트리로 이동합니다.
왼쪽 자식이 None인 경우에는 새로운 노드를 생성하여 연결합니다.
그렇지 않은 경우에는 왼쪽 자식 노드에 대해 재귀적으로 _insert_recursive 를 호출합니다. - 데이터가 현재 노드의 데이터보다 크면
오른쪽서브트리로 이동합니다
오른쪽 자식이 None인 경우에는 새로운 노드를 생성하여 연결합니다.
그렇지 않은 경우에는 오른쪽 자식 노드에 대해 재귀적으로 _insert_recursive를 호출합니다. - 데이터가 이미 트리에 존재하는 경우에는 아무 작업도 수행하지 않습니다.
삭제(Delete)
def delete(self,value):
self.root = self._delete_recursive(self.root,value)
def _delete_recursive(self,root,value):
if root is None:
return root
if value < root.data:
root.left = self._delete_recursive(root.left,value)
elif value > root.data:
root.right = self._delete_recursive(root.right,value)
else:
if root.left is None:
return root.right
elif root.right is None:
return root.left
root.data = self._get_min_value(root.right)
root.right = self._delete_recursive(root.right,root.data)
return root
def _get_min_value(self,root):
while root.left is not None:
root = root.left
return root.data
- delete(self, value)
- 이 메서드는 BST에서 주어진 값을 삭제합니다.
- 먼저 self.root를 업데이트하기 위해 _delete_recursive 메서드를 호출합니다.
- _delete_recursive(self,root,value)
- 이 메서드는 실제 재귀적으로 값을 삭제하는 역할을 합니다.
- root는 현재 서브트리의 루트 노드를 가리키며 value는 삭제할 값을 나타냅니다.
- 먼저 root가 None이면 아무 작업 없이 root를 반환합니다.(삭제할 값이 트리에 없는 경우)
- 만약 삭제할 값이 현재 노드의 데이터보다 작으면
왼쪽서브트리에서 값을 삭제하도록 재귀 호출합니다.
삭제 후에는 왼쪽 자식 노드를 반환하여 현재 노드의 왼쪽 자식으로 연결합니다. - 값이 현재 노드의 데이터보다 크면
오른쪽서브트리에서 값을 삭제하도록 재귀 호출합니다.
마찬가지로 삭제 후에는 오른쪽 자식 노들르 반환하여 현재 노드의 오른쪽 자식으로 연결합니다. - 삭제할 값을 찾은 경우에는 다음과 같이 처리합니다.
현재 노드의 왼쪽 자식이 None이면,오른쪽 자식을 반환하여 현재 노드의 자리를 대체합니다.
현재 노드의 오른쪽 자식이 None이면,왼쪽 자식을 반환하여 마찬가지로 현재 노드의 자리를 대체합니다. - 양쪽 자식이 모두 존재하는 경우에는
오른쪽서브트리에서 가장 작은 값을 찾아 현재 노드의 데이터를 그 값으로 대체하고, 오른쪽 서브트리에서 그 값을 삭제합니다.
- _get_min_value(self,root)
- 이 메서드는 주어진 서브트리에서 가장 작은 값을 찾아 반환합니다.
while root.left is not None은 현재 노드의 왼쪽 자식이 None이 아닌 동안 계속 반복하여 왼쪽 자식으로 이동합니다.- BST에서 가장 작은 값은 왼쪽 자식 노드의 가장 왼쪽에 위치한 값입니다.
- 따라서 왼쪽 자식 노드로 계속 이동하며 가장 작은 값을 찾아 반환합니다.
- 최종적으로 가장 작은 값을 가진 노드의 data를 반환합니다.
검색(Search)
def search(self,value):
return self._search_recursive(self.root, value)
def _search_recursive(self, root, value):
if root is None or root.data == value:
return root
if value < root.data:
return self._search_recursive(root.left,value)
return self._search_recursive(root.right,value)-
search 메서드는 BST에서 주어진 값(value)를 찾기 위해 _serach_recursive 메서드를 호출합니다.
-
여기서 매개변수 value는 BST에서 찾고자 하는 값입니다
-
search_recursive는 실제 재귀적으로 BST를 탐색하여 주어진 값(value)을 찾습니다.
-
root는 현재 서브 트리의 루트 노드입니다. 초기에는 BST의 전체 루트(self.root)로 시작하며, 재귀 호출 시 해당 서브트리의 루트로 갱신됩니다. value는 위와 동일하게 찾고자 하는 값입니다.
-
root가 None인 경우 BST가 비어 있거나 해당 값을 가진 노드를 찾지 못한 경우 -> 이 경우 None을 반환합니다
orroot.data == value 인 경우 해당 노드의 데이터가 찾는 값과 일치하는 경우 -> 해당 노드를 반환합니다. -
value < root.data 인 경우 : 찾고자 하는 값이 현재 노드의 데이터보다 작으므로,
왼쪽 자식 노드에서 재귀적으로 탐색을 진행합니다. -
그 외의 경우 (value > root.data) : 찾고자 하는 값이 현재 노드의 데이터보다 크거나 같으므로,
오른쪽 자식 노드에서 재귀적으로 탐색을 진행합니다. -
_search_recursive 메서드는 재귀적인 방식으로 동작하여, 현재 노드의 데이터와 찾고자 하는 값(value)을 비교합니다.
-
재귀 호출을 통해 각 서브트리에서도 동일한 비교와 탐색 작업을 수행하며 BST의 특성에 따라 왼쪽 또는 오른쪽 자식 노드로 이동합니다.
전위 순회(Preorder Traversal)
def preorder_traversal(self):
result = []
self._preorder_recursive(self.root, result)
return result
def _preorder_recursive(self, root, result):
if root is not None:
result.append(root.data)
self._preorder_recursive(root.left, result)
self._preorder_recursive(root.right, result)전위 순회는 루트 노드를 먼저 방문한 후 왼쪽 서브트리를 순회하고, 그 다음에 오른쪽 서브트리를 순회하는 방식입니다.
-
preorder_traversal 메서드는 이진 트리의 전위 순회 결과를 반환합니다.
-
변수 result 는 전위 순회 결과를 저장하는 리스트입니다.
-
전위 순회를 수행한 결과인 result 리스트를 반환합니다.
-
_preorder_recursive 메서드는 재귀적으로 이진 트리를 전위 순회합니다.
-
매개변수는 위와 비슷합니다.
root: 현재 순회하고 있는 서브트리의 루트 노드입니다. 초기에는 전체 트리 의 루트(self.root)로 시작하며, 재귀 호출 시에는 순회 중인 서브트리의 루트가 됩니다.
result: 전위 순회 결과를 저장할 리스트입니다.
if root is not None : 현재 노드(root)가 None이 아닌지 확인합니다.
None인 경우에는 리프 노드나 자식이 없는 노드입니다. 재귀 호출을 계속하기 전에 이 조건을 확인하여 작업을 중지합니다.
result.append(root.data) : 현재 노드의 데이터를 result 리스트에 추가합니다.
이는 전위 순회의 특성에 따라 먼저 루트 노드를 방문하고 데이터를 처리하는 단계입니다..
self._preorder_recursive(root.left, result): 현재 노드의 왼쪽 자식 노드로 재귀 호출을 수행합니다. 이는 왼쪽 서브트리를 전위 순회하는 과정입니다. 왼쪽 자식이 None이면 해당 부분은 스킵됩니다.
- right도 마찬가지입니다.
중위 순회(Inorder Traversal)
def inorder_traversal(self):
result = []
self._inorder_recursive(self.root, result)
return result
def _inorder_recursive(self, root, result):
if root is not None:
self._inorder_recursive(root.left, result)
result.append(root.data)
self._inorder_recursive(root.right, result)중위 순회가 전위 순회와의 다른 점은
result.append(root.data) 가
왼쪽 서브트리를 모두 순회한 후 현재 노드를 방문한다는 것입니다.
후위 순회(Postorder Traversal)
def postorder_traversal(self):
result = []
self._postorder_recursive(self.root, result)
return result
def _postorder_recursive(self, root, result):
if root is not None:
self._postorder_recursive(root.left, result)
self._postorder_recursive(root.right,result)
result.append(root.data)result.append(root.data)가
왼쪽 서브트리를 후위 순회한 뒤에 오른쪽 서브트리를 후위 순회하고,
마지막으로 루트 노드를 방문하게 됩니다.
