최대 힙_ 삽입,추출

🔎 힙이란?

• 힙은 데이터에서 최대값과 최소값을 빠르게 찾기 위해 고안된 완전 이진 트리(Complete Binary Tree)입니다.

• 힙은 항상 큰 값이 상위 레벨에 있고 작은 값이 하위 레벨에 있도록 하는 자료구조입니다.
  부모 노드의 값이 자식 노드의 값보다 항상 커야 합니다.
  그러면 가장 큰 값은 모든 자식보다 커야 하기 때문에 가장 위로 갈 것입니다.
  따라서 최대의 값들을 빠르게 구할 수 있게 되는 것입니다.

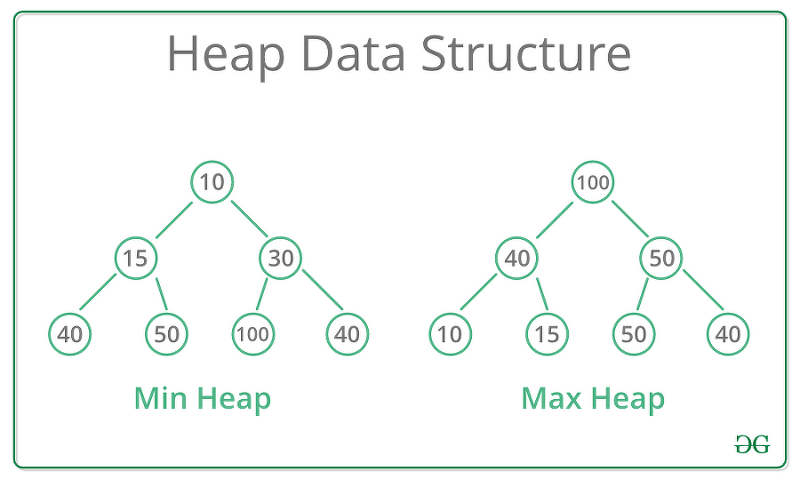
참고로, 힙은 다음과 같이 최대값을 맨 위로 올릴 수도 있고, 최소값으르 맨 위로 올릴 수도 있습니다.

최대값이 맨 위인 힙을 max 힙, 최소값이 맨 위인 힙을 Min힙이라고 합니다.

최대(Max) 힙- 삽입 알고리즘

• 힙은 항상 큰 값이 상위 레벨에 있고 작은 값이 하위 레벨에 있어야 합니다.
  따라서, 원소를 추가하거나 삭제할때도 위의 규칙이 지켜져야 합니다.

1. 원소를 맨 마지막에 넣습니다.
2. 그리고 부모 노드와 비교합니다. 만약 더 크다면 자리를 바꿉니다
3. 부모 노드보다 작거나 가장 위에 도달하지 않을 때까지 2의 과정을 반복합니다.

class BinaryMaxHeap:
    def __init__(self):
        self.items = [None]
        # 계산 편의를 위해 인덱스는 1부터 사용한다.
        # None, (1), 2, 3, 4 ->

    def insert(self,k):
        self.items.append(k) # 새로운 요소를 힙의 마지막에 추가한다.
        self._percolate_up() # 새로 추가된 요소의 힙을 적절한 위치에 올려준다.

    def _percolate_up(self):
        cur = len(self.items) - 1 # 새로 추가된 요소의 인덱스를 cur로 설정한다.
        parent = cur // 2 # cur의 부모 노드 인덱스를 계산한다
                        # 부모의 값을 2로 나누고 나머지 값을 버립니다.
        while parent > 0:
            if self.items[cur] > self.items[parent]: # 부모보다 나의 값이 더 클 경우
                self.items[cur], self.items[parent] = self.items[parent],self.items[cur]
                # 부모와 나의 값의 자리를 바꾼다.

            cur = parent # 나의 위치를 부모로 바꿔줍니다.
            parent = cur // 2 # 부모의 값을 2로 나누고 나머지 값을 버립니다.

            # parent가 0보다 클때까지 반복

insert 메서드는 힙에 새로운 요소 'k'를 추가하는 역할을 한다.
self.items.append(k) 를 통해 새로운 요소를 힙의 맨 끝에 추가한다.
추가한 후에는 _percolate_up 메서드를 호출하여 새로 추가된 요소를 적절한 위치로 올려준다.

_percolate_up 메서드는 새로 추가된 요소를 힙의 적절한 위치로 올려주는 메서드이다.
cur 변수에는 새로 추가된 요소의 인덱스를 저장한다.
parent 변수에는 cur의 부모 노드 인덱스를 계산하여 저장한다.
* parent = cur // 2
부모의 값을 2로 나누고 나머지 값을 버린다.

while parent > 0: 루프를 통해 부모 노드가 존재하고,
부모보다 큰 경우에는 위치를 교환하는 작업을 반복한다.

self.items[cur] > self.items[parent] 조건을 통해
새로 추가된 요소가 부모보다 크면 두 요소의 위치를 바꾼다.

이후 cur을 parent로 업데이트하고, parent를 새로운 cur의 부모 인덱스로 업데이트하여 ( cur // 2 ) 다음 루프를 준비한다.

insert 메서드를 호출하면 새로운 요소가 힙에 추가되고,
_percolate_up 메서드를 통해 힙의 특성을 유지하면서 요소가 올바른 위치로 이동된다.

최대(Max) 힙- 추출 알고리즘

• 최대 힙에서 원소를 추출하는 방법은 최대값, 루트 노드를 삭제하는 것입니다.
  스택(Stack)과 같이 맨 위에 있는 원소만 제거할 수 있고, 다른 위치의 노드는 삭제할 수는 없습니다.
  또한 맥스 힙에 원소를 추가했던 것과 마찬가지로 원소를 삭제할 때도 힙의 규칙이 지켜져야 합니다.

1. 루트 노드와 맨 끝에 있는 원소를 교체한다.
2. 맨 뒤에 있는 원소(원래의 루트 노드)를 삭제한다.
3. 변경된 노드와 자식 노드들을 비교합니다. 두 자식 중 더 큰 자식과 비교해서 자신보다 자식이 더 크다면 자리를 바꿉니다.
4. 자식 노드 둘 보다 부모 노드가 크거나 가장 바닥에 도달하지 않을 때까지 3의 과정을 반복합니다.
5. 2에서 제거한 원래의 루트 노드를 반환합니다.

    def extract(self):
        if len(self.items) - 1 < 1 :
            return None

        root = self.items[1] # self.item[1] 은 최대 힙의 루트에 있는 요소로, 이를 root 변수에 저장한다.
        self.items[1] = self.items[-1] # 힙의 마지막 요소(self.items[-1])를 루트로 옮긴다. 
		#힙의 삭제 작업 중 루트를 제거하고 힙의 성질을 유지하기 위한 과정이다.
        self.items.pop() # 힙에서 루트(최대값)을 제거한다.
        self._percolate_down(1) # 루트에서부터 최대 힙의 성질을 유지하도록 요소를 아래로 내린다.
        return root # 힙의 구조를 만들고 루트를 반환

    def _percolate_down(self,cur):
        biggest = cur
        left = 2 * cur
        right = 2 * cur + 1

        # 왼쪽 자식이 힙 배열의 범위 내에 있고, 왼쪽 자식이 현재 가장 큰 값보다 크면 biggest를 왼쪽 자식으로 업데이트한다.
        if left <= len(self.items) - 1 and self.items[left] > self.items[biggest]:
            biggest = left

        # 오른쪽 자식이 힙 배열의 범위 내에 있고, 오른쪽 자식이 현재 가장 큰 값보다 크면 biggest를 오른쪽 자식으로 업데이트한다.
        if right <= len(self.items) - 1 and self.items[right] > self.items[biggest]:
            biggest = right

        if biggest != cur:
            # 현재 노드와 biggest 노드의 값을 교환한다. (최대 힙의 성질을 만족하기 위해)
            self.items[cur], self.items[biggest] = self.items[biggest], self.items[cur]
            # biggest 노드에서부터 다시 _percolate_down을 호출하여 하위 서브트리에 대해 최대 힙의 성질을 유지한다.
            self._percolate_down(biggest)

🤕