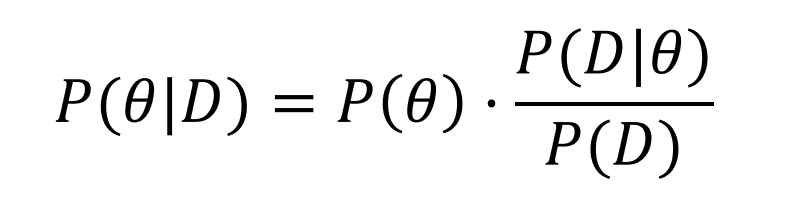Intro
1주 차 회고 ①에 이어 AI 기초 수학 강의를 들으며 중요한 부분 및 부족한 부분을 기록하고자 한다.
AI Math
1. 벡터
- 벡터 원소 개수가 벡터의 차원임 (열벡터, 행벡터 모두)
- 벡터는 공간에서 한 점을 나타내며, 원점으로부터 상대적 위치를 표현
- 벡터에 스칼라를 곱해주면 방향은 그대로, 길이만 변함
- 벡터가 같은 모양을 가지면 성분곱(element-wise)을 계산할 수 있음
- 노름(norm)은 원점에서부터 거리를 뜻함
L1 노름은 각 성분의 절대값을 모두 더함
L2 노름은 유클리드 거리를 계산
노름의 종류에 따라 기하학적 성질이 달라짐 (L1 norm: Lasso 회귀, L2 norm: Ridge 회귀)
- 두 벡터 사이의 거리는 뺄셈으로 구함
내적
- cosθ 는 두 벡터는 어느 차원에 있어도 가능하지만, L2 norm을 이용해서만 가능
- cosθ = 두 벡터의 내적/두 벡터의 거리 곱
- Proj(x) = ||x||cosθ
- <x, y> = ||y||Proj(x) = ||x||·||y|| cosθ
내적은 두 벡터의 유사도를 측정할 때 사용
cos값은 각도가 0일수록 크다(내적 값이 크다) -> 두 벡터 사이의 거리가 가깝다 -> 유사하다
2. 행렬
- 벡터가 공간에서 한 점을 의미한다면, 행렬은 여러 점들을 나타냄
- Numpy의 inner 함수는 두 행렬의 행벡터를 내적해서 구함
- 행렬곱은 한 행렬의 행벡터와 다른 행렬의 열벡터의 내적이므로 XYT로 구해야 함 or X@Y
- 행렬곱을 통해 벡터를 다른 차원의 공간으로 보낼 수 있음 (선형변환)
- Numpy의 np.linalg.inv(X) 이용해서 역행렬 계산 가능
- 역행렬은 행과 열의 개수가 같아야 하며, det(A)가 0이 아니어야 함
유사역행렬
- 행과 열의 개수가 다른 경우 유사역행렬 또는 무어펜로즈 역행렬 A+ 을 사용한다.
- 행의 개수가 더 많으면 A+= (ATA)-1 AT
열의 개수가 더 많으면 A+= AT (AAT)-1- Numpy의 np.linalg.pinv(X) 이용
- 변수 개수가 식의 개수보다 많은 연립방정식의 해를 찾거나 선형 회귀식을 찾는데 사용
3&4. 경사하강법
- 미분은 sympy의 sympy.diff를 이용해 계산 가능
- 미분값을 더해주면 함수 값이 증가하고, 빼면 함수 값 감소
- 미분값을 더하는 것을 경사상승법(gradient ascent)이라 하며, 함수 극대값의 위치를 구할 때 사용(목적함수 최대화)
- 미분값을 더하는 것을 경사하강법(gradient descent)이라 하며, 함수 극소값의 위치를 구할 때 사용(목적함수 최소화)
- 극값에 도달하면 미분값이 0이므로 경사 상승/하강법 모두 움직임이 멈추게 된다.
- 변수가 벡터라면 편미분을 사용
- 각 변수 별로 편미분을 계산한 벡터를 그레디언트 벡터라고 함
선형회귀 경사하강법
- 선형회귀 목적식은 target과 predict 사이의 L2-norm이며, 이를 최소화하는 coefficient를 구하기 위해 그레디언트 벡터를 계산해야 한다.
import numpy as np X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]]) y = np.dot(X, np.array([1, 2])) + 3 # [3 5 6 8] + 3 = [6 8 9 11] ''' dot, @: 행렬곱(=내적) 베타 = [1, 2, 3]이며 3의 경우 y절편(intercept)으로 dot 연산에 직접 들어가지 않는다 ''' X = np.array([np.append(x, [1]) for x in X]) # [[1, 1, 1], [1, 2, 1], [2, 2, 1], [2, 3, 1]] ''' y절편(intercept) 항 추가를 위해 1을 append ''' beta_gd = [-10, -15, 7] # initial coefficient for _ in range(5000): error = y - X @ beta_gd grad = - X.T @ error beta_gd = beta_gd - 0.01 * grad print(beta_gd) # [0.99999742 2.00000036 3.0000034 ] ''' 우리가 구하고자 하는 target coefficient는 [1, 2, 3]이다. => X 데이터를 가장 잘 설명할 수 있는 선형 회귀식의 coefficient를 [1, 2, 3]으로 지정하고, 초기 coefficient는 아무 값이나 지정한다. 그 후 선형회귀 목적식에서 베타의 gradient를 이용해 경사하강법 진행 '''확률적 경사하강법
- 모든 데이터를 사용하지 않고 데이터를 한 개(SGD) 또는 일부(mini-batch SGD)만 사용해 업데이트
- mini batch를 확률적으로 선택하므로 목적식 모양이 계속 바뀌게 된다.
- minimum으로 향하는 그래디언트 방향이 유사
- non-convex 함수에서 local minimum에서 탈출할 수 있음
5. 딥러닝 학습방법
O(output) = X(input) · W(weight) + b(bias)
- 가중치 행렬 W는 데이터 행렬 X를 다른 공간으로 보내는 역할
- b행렬은 각 행이 모두 같은 행렬
softmax
- 모델의 출력을 확률로 변환(특정 클래스에 속할 확률) -> softmax(Wx+b)
- 학습에는 softmax, 추론의 경우는 원-핫 벡터 이용
activation function
- 신경망은 선형모델과 활성함수(activation function)를 합성한 함수
- 활성함수는 비선형 함수로서 선형 모델로 나오는 각각 원소에 취해지는 함수
- softmax는 모든 값을 고려해서 출력을 하는 반면, 활성함수는 다른 주소의 출력 값은 신경 쓰지 않고 해당 주소 출력 값만 고려해서 계산
인풋 값으로 벡터가 아닌 실수- 선형 모델로 나온 출력물을 비선형 모델로 변환시키며, 이 변환된 벡터를 잠재 벡터 or 히든 벡터라 함
- 활성함수를 사용하지 않으면 선형 모형과 차이가 없음
6. 확률론
확률분포 & 확률변수
- 확률분포는 데이터의 초상화
- 데이터만 가지고 확률분포(D)를 아는 것은 불가능하며, 기계학습 모형을 이용해 추론
확률변수는 데이터 공간 상에서 관측 가능한 데이터이며, 함수에 해당한다. (x, y) ~ D- 데이터 공간 상에서 데이터를 추출할 때 확률변수를 사용, 확률변수로 추출한 데이터의 분포를 확률분포라 한다.
- 확률변수가 이산확률변수인지, 연속확률변수인지는 데이터 공간에 의해 결정되는 것이 아니라 확률분포 D에 의해 결정된다.
Ex) -0.5 ~ 0.5 사이 실수들 중 정수를 골라라 : 데이터 공간은 연속형이나 D는 이산형- 모든 확률변수가 이산 또는 연속확률변수인 것은 아니다.
결합분포
- 결합분포 P(x, y) : 동일한 표본공간에서 정의되는 두 개 이상의 확률변수의 분포
- 원래 데이터의 확률분포 D가 이산형(연속) 분포라 해서 결합분포도 이산형(연속)은 아니다.
- P(x)는 x에 대한 주변확률분포로 y에 대한 정보를 주진 않는다.
조건부확률분포
- 특정 클래스가 주어진 조건에서 데이터의 확률분포를 보여줌
e.g. Y가 1인 조건이 주어졌을 때의 조건부확률분포- 조건부확률 P(y|x)는 입력변수 x에 대해 정답이 y일 확률을 의미
- softmax 함수는 특징벡터가 주어졌을 때 정답 y를 계산한다.
- 회귀 문제에선 조건부기대값 E[y|x]을 추정
기대값은 여러 통계랑을 계산할 수 있는 데이터를 대표하는 통계량몬테카를로 샘플링
- 몬테카를로 샘플링은 확률변수가 모두 독립 + 동일한 확률분포(i.i.d)임이 보장되어야 함
e.g. 주사위 던지기는 모든 경우가 독립적이며 나올 확률도 1/6으로 i.i.d이다
7. 통계학
- 데이터가 특정 확률분포를 따른다고 선험적으로 가정한 후, 그 분포를 결정하는 모수(파라미터)를 추정하는 방법을 모수적 방법론이라 함
- 특정 확률분포를 가정하지 않고 데이터에 따라 모델 구조 및 모수 개수가 유연하게 바뀌면 비모수 방법론이라 함 (모수를 사용하지 않는 것이 아닌 개수가 유연하게 바뀜)
확률분포 가정하는 방법
- 데이터를 생성하는 원리를 먼저 고려하고 확률분포 가정
- 모수 추정 후에 반드시 각 분포에 맞는지 검정
- 확률분포 가정 후 모수를 추정할 수 있음
- 정규분포의 경우 표본평균, 표본분산을 구하여 모수 추정
- 통계량(표본평균, 표본분산)의 확률분포를 표집분포(sampling distribution)이라 하며, sample distribution(표본분포)과 다르다. 표집분포에서 sample size N이 커질수록 정규분포를 따르며, 이를 중심극한정리라 칭함
- 표본평균·분산은 모집단에서 N개의 표본을 뽑을 때마다 같을 수도, 다를 수도 있다 (확률변수)
- 모집단의 분포가 정규분포를 따르지 않으면 표본분포는 정규분포를 따르지 않는다. 하지만 표집분포는 정규분포를 따른다.
최대가능도 추정법(MLE)
- 이론적으로 가장 가능성이 높은 모수를 추정하는 방법
- 모수 추정은 실현된 표본값 X는 알고 있지만 모수 θ를 모름
- 확률함수에서 모수를 변수로 보는 경우 이 함수를 가능도함수라고 한다.
- 확률함수 P(x; θ) = 가능도함수 L(θ;x)
- x는 확률분포가 가질 수 있는 실수값으로, 스칼라 값일수도 있고 벡터 값일수도 있음
- 확률밀도함수는 적분하면 전체 면적이 항상 1이지만, 가능도함수는 1이 된다는 보장이 없음
로그가능도함수
- 데이터 집합 X가 독립적으로 추출되었을 경우 로그가능도를 최적화
- 모수 θ가 주어졌을 때 확률분포함수의 곱을 이용해 가능도를 계산하고, 이를 최대가 되게 하는 θ를 구함
- 식에 로그를 취해 곱셈을 덧셈으로 바꿔 연산량을 줄임
확률분포의 거리
- 데이터 공간에 두 개의 확률분포 P(x), Q(x)가 있을 경우 두 확률분포 사이의 거리를 계산
- 분류 문제에서 정답레이블을과 모델 예측 확률분포 사이의 최대가능도 추정법은 쿨백-라이블러 발산을 최소화하는 것과 동일
8. 베이즈 통계학
베이즈 정리 공식
D: 새로 관찰하는 데이터
θ: 가설, 모수
P(θ|D) 사후확률 : 데이터를 관찰했을 때 가설, 파라미터가 성립할 확률
P(θ) 사전확률 : 데이터가 주어지지 않은 상황에서 사전에 주어진 확률
P(D|θ) 가능도 : 현재 가설에서 데이터가 관찰될 확률
P(D) Evidence : 데이터 자체 분포베이즈 정리 특징
- 베이즈 정리를 통해 새로운 데이터가 들어왔을 때 앞서 계산한 사후확률을 사전확률로 사용하여 갱신된 사후확률 계산 가능
- 조건부 확률은 인과관계를 추론할 때 함부로 사용해서는 안 됨
- 유입되는 데이터 분포가 바뀌면 조건부확률 기반 예측모형을 이용할 시 정확도가 떨어질 수 있음
인과관계 기반의 예측모형을 만들어야 함 (여러 시나리오가 발생해도 정확도가 크게 변하지 않음)
10. RNN
- 시퀀스 데이터: 소리, 문자열, 주가 등 순차적으로 들어오는 데이터
시퀀스 데이터는 독립동등분포(i.i.d)의 가정을 잘 위배하기 때문에 순서를 바꾸거나 과거 정보에 손실이 발생하면 데이터의 확률분포도 바뀌게 됨- 시퀀스 데이터를 다루기 위해선 길이가 가변적인 데이터를 다룰 수 있는 모델 필요
- W(2), WH(1), W(2)과 같은 가중치 행렬은 시점 t에 영향을 받지 않고 불변
RNN의 역전파(BPTT, Backpropagation Through Time)
- 잠재변수 H에는 다음 시점의 잠재변수의 그래디언트 벡터와 해당 시점의 출력 벡터의 그래디언트 두 개를 전달받는다.
- 그래디언트를 모두 곱해주기 때문에 그 값이 매우 커지거나 매우 작아질 수 있다.
따라서 모든 t시점에 BPTT를 적용하면 학습이 불안정해지기 쉽다. (Gradient Vanish, 기울기 소실)
-> truncated BPTT 사용
truncated BPTT: 특정 시점에서 역전파를 끊음- 또는 LSTM, GRU 사용
회고
강의 학습
기초 강의라 다 알 것이라는 안일한 생각으로 강의를 들었고, 모르는 것이 너무 많은 내 자신을 발견할 수 있었다. 학부생 강의에서 들었던 내용은 맞지만 제대로 이해하고 기억하고 있는 것이 거의 없을 정도였다. 모르는 내용을 최대한 이해하려 했지만, 아직도 제대로 이해하고 넘어간 것인지에 대해선 잘 모르겠다. 어떻게 공부해야 하는가에 대해 감을 잡아가고 있고, 이를 바탕으로 남은 강의도 나만의 학습 방식으로 잘 이해해보려 한다.
피어세션
모르는 사람들과 매일 한 시간 이상 학습 내용 공유, 질의응답, 계획 수립 등 이야기를 나누는 시간을 갖게 됐다. 처음에는 크게 달갑지 않은 활동이었다. 내성적인 성격에 말도 많지 않아 팀에 안 좋은 영향을 가져다 주면 어떡하지라는 고민이 많았지만, 짧은 5일이라는 시간동안 내 생각은 바뀌었다. 배울 것이 많은 팀원들과 토의하며 얻는 것이 많았고, 앞으로도 끊임없이 같이 성장할 계획이다.
마스터 클래스, 오피스 아워, 멘토링
마스터님께서 직접 1시간 동안 실시간으로 특강을 해 주셨고, 지금 내 상황에 있어 너무 유익한 정보들을 많이 들을 수 있었다. 다른 캠퍼분들도 나와 같이 취업과 대학원 진학 두 개에 대해 깊게 고민하고 계셨고, 관련된 질문들과 마스터님의 대답을 통해 내가 몰랐던 부분들도 알게 돼서 너무 뜻깊었다. 그 외 오피스 아워, 멘토링 시간에서도 조교님들의 수준 높은 강의와 조언들, 앞으로 우리 캠퍼들이 나아가야 할 방향을 정해주시며 조금씩 부캠에 적응할 수 있게 됐다.