정렬 알고리즘

파이썬 정렬 알고리즘들을 정리하고자 한다.

1. 버블 정렬

1) 배열의 두 번째 수부터 왼쪽 수와 비교를 진행한다. 두 수 비교 후 더 작은 값을 왼쪽으로 이동시킨다.
2) 1회 반복하면 가장 큰 수가 가장 오른쪽으로 이동한다.
3) (총 배열의 길이 -1) 횟수만큼 반복하면 모든 수가 정렬된다.

따라서 시간복잡도는 O(n-1 + n-2 + ··· + 1 ) = O(N^2)

---

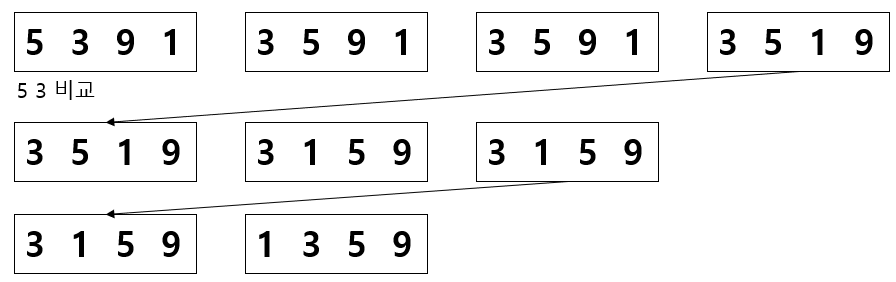
2. 선택 정렬

1) 전체 배열에서 가장 작은 값을 맨 앞의 값과 바꾼다.
2) 그 다음 가장 작은 값과 2번째 인덱스에 존재하는 값을 바꿔준다.
3) 해당 과정을 반복한다.

따라서 시간복잡도는 O(n-1 + n-2 + ··· + 1 ) = O(N^2)

---

3. 삽입 정렬

1) 두 번째 값부터 시작하여 앞의 값과 비교해 앞의 값 왼쪽에 위치할 것인지, 오른쪽에 위치할 것인지 판단한다.
2) 모든 값에 대해 해당 과정을 반복한다.

따라서 시간복잡도는 O(n-1 + n-2 + ··· + 1 ) = O(N^2)

---

4. 퀵 정렬

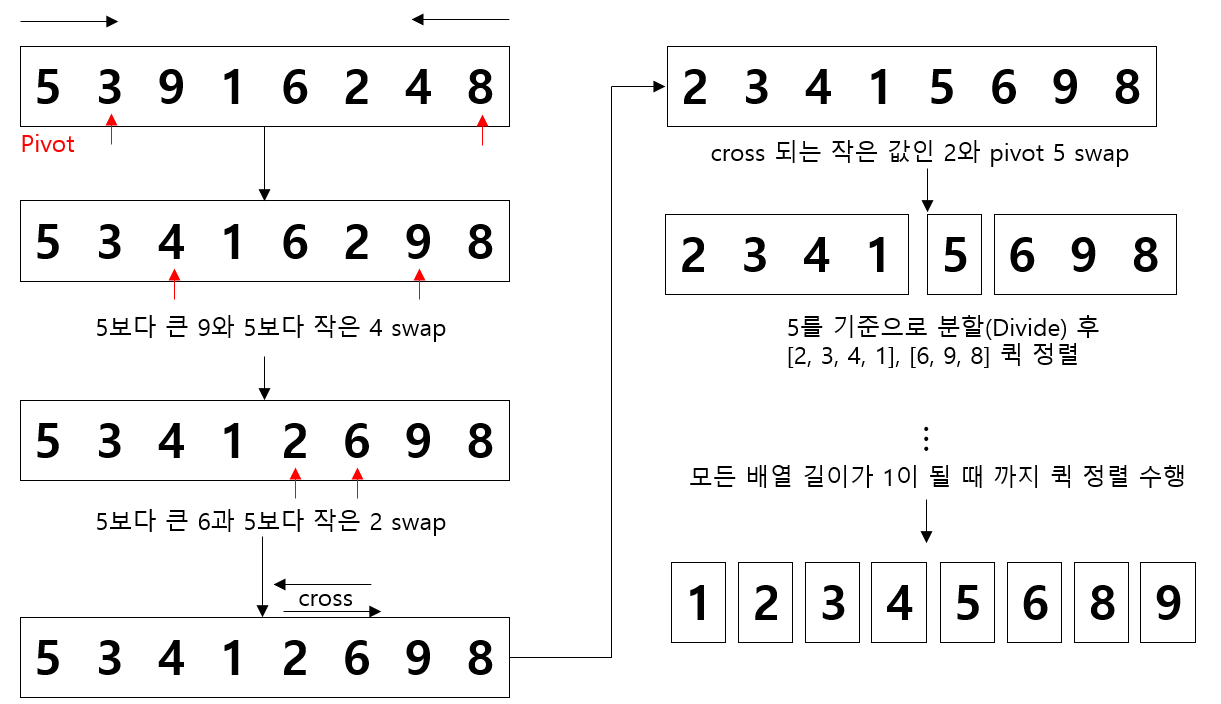
1) pivot 값을 지정한다. 보통 배열의 맨 앞 값으로 지정
2) pivot을 제외한 배열에서 맨 앞과 맨 뒤에서부터 pivot과 크기를 비교한다.
3) left search에선 pivot보다 작은 값을, right search에선 pivot보다 큰 값이 존재해야 한다.
4) left search 중 pivot보다 큰 값이 탐색되면 right search 중 탐색된 pivot보다 작은 값과 swap한다.
5) 이 때 left search와 right search가 cross되면, cross되는 값 중 작은 값과 pivot을 교체한다.
6) pivot 교체 후 배열을 pivot보다 큰 원소 배열과 작은 원소 배열로 분할한다.
7) 해당 과정을 반복하며 모든 배열의 크기가 1 이하가 되면 종료시킨다.

---

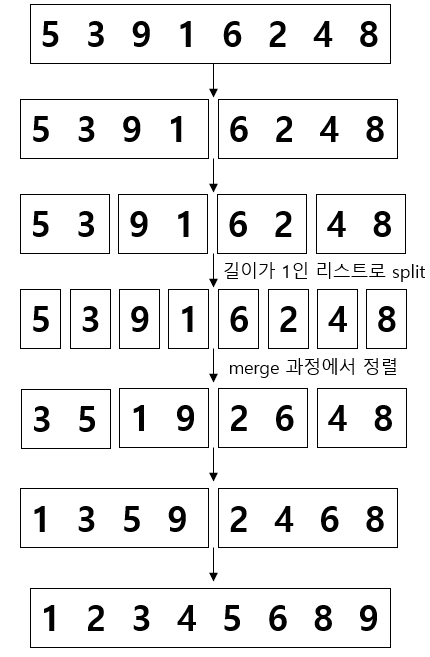
5. 병합 정렬

1. 배열을 길이가 1인 배열로 모두 쪼갠다.
2. 합치는 과정에서 정렬한다.

병합정렬의 경우 처음에 코드가 잘 이해가 되지 않았었다.

Code

def merge_sort(arr):
    if len(arr) < 2:
        return arr

    mid = len(arr) // 2
    low_arr = merge_sort(arr[:mid])
    high_arr = merge_sort(arr[mid:])

    merged_arr = []
    l = h = 0
    while l < len(low_arr) and h < len(high_arr):
        if low_arr[l] < high_arr[h]:
            merged_arr.append(low_arr[l])
            l += 1
        else:
            merged_arr.append(high_arr[h])
            h += 1
    merged_arr += low_arr[l:]  # ··· ⓐ
    merged_arr += high_arr[h:]  # ··· ⓑ 
    return merged_arr

만약 low_arr = [0, 1], high_arr = [2, 3, 4, 5]라면 l=2에서 while문 조건에 의해 merged_arr = [0, 1, 2, 3]으로 루프를 탈출한다.
이 때 high_arr의 남은 [3, 4] extend를 위해 ⓐ, ⓑ와 같은 코드를 작성해야 한다.