방의 개수
처음에는 해당 문제의 테스트 케이스를 보면서 간단하게 arrows를 순회하면서 해당 정점이 방문한 정점인가를 체크하면 되는 거 아닌가? 라는 생각을 했다. 그렇지만 단순히 방문 여부만으로는 부족했다. 예를 들어 arrows가 똑같은 사각형을 두 번 그리는 것이라면? 일 때 문제가 발생한다. 그래서 여기서 하나 더 추가해줘야 할 것이 방문 여부에 다가 해당 경로로 방문한 적이 있는 가이다.
여기까지는 문제가 없었는데 계속 제출해도 실패했다. 그 원인을 보니 정점이 아닌 곳에서도 방이 생길 수 있다는 것이었다. (이 부분은 검색을 통해 파악함.) 그래서 이 부분을 해결하기 위해 크기를 늘리는 것!
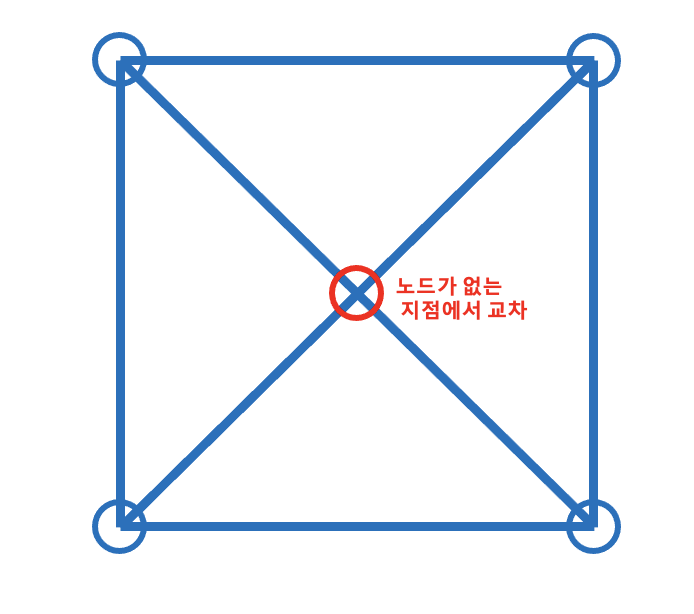
즉 크기가 두 배가 되면 노드가 없는 지점에서 교차하는 부분이 노드가 되기 때문이다!
def solution(arrows):
answer = 0
x,y = 0,0
edge = {}
dirx = [0,1,1,1,0,-1,-1,-1]
diry = [1,1,0,-1,-1,-1,0,1]
edge[(0,0)] = set()
for ar in arrows:
for _ in range(2): # 크기를 늘리는 부분
nextx,nexty = x + dirx[ar], y + diry[ar]
if (nextx,nexty) in edge and (x,y) not in edge[(nextx,nexty)] :
answer += 1
edge[(x,y)].add((nextx,nexty))
edge[(nextx,nexty)].add((x,y))
elif (nextx,nexty) not in edge:
edge[(nextx,nexty)] = set([(x,y)])
edge[(x,y)].add((nextx,nexty))
x,y = nextx,nexty
return answer아이템 줍기
아이템 줍기 문제도 비슷한 아이디어가 사용된다.
https://jyeonnyang2.tistory.com/247 이 분 글을 참고해서 보면
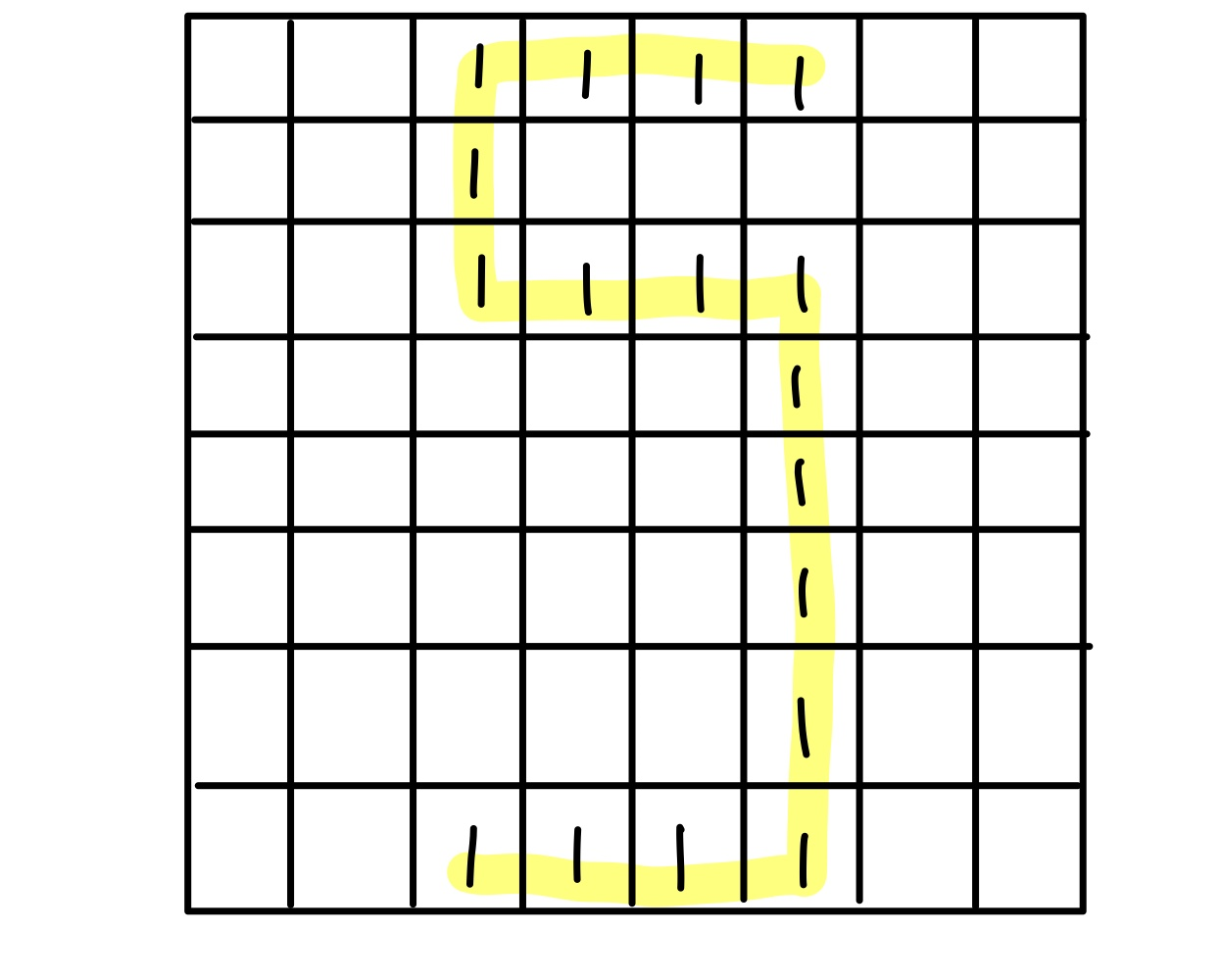
왼쪽 경로가 원래대로 의도한 경로인데, 실제로는 오른쪽처럼 구해진다는 것이다. 왜냐하면 사각형을 채우고 나서 컴퓨터는 start - end 까지 최단 경로를 bfs로 구하면 오른쪽으로 구하는게 당연하다. 하지만 우리가 원하는 것은 그것이 아니기 때문에..
그래서 이 문제도 마찬가지로 경로를 2배씩 늘려주면 해당 문제를 해결할 수 있다.

from collections import deque
def solution(rectangle, characterX, characterY, itemX, itemY):
answer = 0
field = [[-1] * 102 for i in range(102)]
for r in rectangle:
# 모든 좌표값 2배
x1, y1, x2, y2 = map(lambda x: x*2, r)
for i in range(x1, x2+1):
for j in range(y1, y2+1):
if x1 < i < x2 and y1 < j < y2:
field[i][j] = 0
# 다른 직사각형의 내부가 아니면서 현재 직사각형의 테두리일 때 1로 채움
elif field[i][j] != 0:
field[i][j] = 1
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
q = deque()
q.append([characterX * 2, characterY * 2])
visited = [[1] * 102 for i in range(102)] # 아직 방문하지 않은 곳은 1로 표시
visited[characterX * 2][characterY * 2] = 0 # 시작 지점은 0으로 초기화
while q:
x, y = q.popleft()
# 도착한 곳이 아이템이 있는 장소라면 현재의 최단거리(나누기 2)를 answer로 하고 while문을 빠져나옴
if x == itemX * 2 and y == itemY * 2:
answer = visited[x][y] // 2
break
# 아니라면 상하좌우를 탐색
for k in range(4):
nx = x + dx[k]
ny = y + dy[k]
# 현재 좌표가 테두리이고 아직 방문하지 않은 곳이라면 q에 추가 후 visited를 최단거리로 갱신
if field[nx][ny] == 1 and visited[nx][ny] == 1:
q.append([nx, ny])
visited[nx][ny] = visited[x][y] + 1
return answer두 문제 모두 쉬운 그래프 문제였으나 2배로 늘리는 아이디어가 잘 떠오르지 않았다.
