알고리즘 11일차 - 그래프, 최단 경로 알고리즘, 다익스트라

놀고 싶은데, 왜 다들 공부하는거야·2021년 4월 28일

다익스트라 알고리즘

알고리즘

목록 보기

11/11

~~피곤하다.. 그래도 해야한다~~

그래프에 관한 알고리즘이 워낙에 많고 시험에도 자주 나오니 대략적으로 정리하면 다음과 같다.

그래프의 순회
1. DFS
2. BFS
그래프의 최단 경로
1. 다익스트라
2. 벨만포드
3. 플루이드 와샬
최소 비용 그래프 연결(MST)
1. 프림
2. 크루스칼
우선 순위에 따른 그래프 탐색
1. 위상 정렬
네트워크 유량

오늘 우리가 배울 것은 그래프의 최단 경로의 다익스트라 알고리즘이다.

0. 개요

그래프의 최단 경로 문제는 간선의 가중치가 주어질 때, 시작 노드에서 임의의 노드까지의 최단 경로를 구하는 알고리즘이다. 임의의 경로는 시작 노드를 제외한 모든 노드가 될 수 있다. 즉, BFS 역시 최단 경로 문제를 해결할 수 있지만, 이는 간선의 가중치가 모두 같을 때만 가능하다.

만약, 간선의 가중치가 서로 다른 값을 가진다면 이 때에는 BFS를 사용할 수 없다. 따라서 우리는 새로운 알고리즘이 필요한데, 이것이 바로 다익스트라, 벨만 포드, 플루이드 와샬 알고리즘이다.

그 중에서도 다익스트라는 특정한 노드에서 시작하여 그래프의 모든 노드로 가는 최단 경로를 구하는 알고리즘으로, 간선의 가중치가 양수일 때만 가능하다.

그렇다면 음수일 때는 어떠한가?? 벨만 포드 알고리즘은 특정한 노드에서 시작하여 그래프의 모든 노드로 가는 최단 경로를 구하는 알고리즘으로, 간선의 가중치가 음수, 양수일 때 모두 가능하다.

여기서 더 발전하여, 특정한 노드에서 시작하는 가정이 아닌, 모든 노드에서 모든 노드까지의 최단 거리를 모두 구하고 싶다면 어떻게 해야할까?? 이 때에는 플루이드 와샬 알고리즘을 사용하면 된다.

따라서 우리는 최단 경로 문제의 가장 기본적인 내용인 다익스트라를 제일 처음에 배우는 것이다.

1. 다익스트라 알고리즘 (Dijkstra)

위에서도 언급하였 듯이 다익스트라 알고리즘은 특정 노드에서 시작하여 그래프의 모든 노드로 가는 최단 거리를 구하는 알고리즘이다.

다익스트라 알고리즘의 원리는 다음과 같다.

시작 노드에서부터, 현재 내가 알고있는 모든 간선을 살펴보고 최단 거리를 갱신한다. 이후, 현재 내가 알고있는 거리 중에 최단 거리를 뽑고 해당 노드를 방문한다. 이렇게 모든 간선을 한 번 이상 방문하여, 현재 내가 알고있는 특정 노드까지의 거리가 최소가 되도록 바꾸는 것이다.

간단하게 보면, greedy와 dp가 적용된 알고리즘이다. 앞에서 greedy와 dp를 배우지 않았는데, 정리하면 greedy는 내가 알고있는 것 중에 최적(여기서는 내가 알고있는 거리 중에 최단 거리)을 선택하는 것이고, dp는 이전에 알고있던 값을 이용하여 값을 갱신한다는 것 (여기서는 특정 노든 A에서 B를 거쳐 C로 간다면 A B까지 가는 거리를 미리 계산해놓고, B C까지의 최단 거리를 새로 갱신한다)는 것이다.

정리하면, 내가 알고있는 것을 이용하여 현재로서는 최선의 최단 거리를 뽑아내지만, 가장 최단 거리로 이동하여 거리를 갱신하다보면, 최선의 최단 거리가 변할 수 있다는 것이다.

예제를 보면서 확인해보자

다익스트라 알고리즘을 위해서는 두 개의 배열이 필요하다.

check 배열 : i번째 노드를 방문했는지 확인하는 배열
dist 배열 : 시작 노드에서부터 i번째 노드까지의 거리를 저장하는 배열

다음의 배열을 참고하여, 예제를 만들어보겠다.

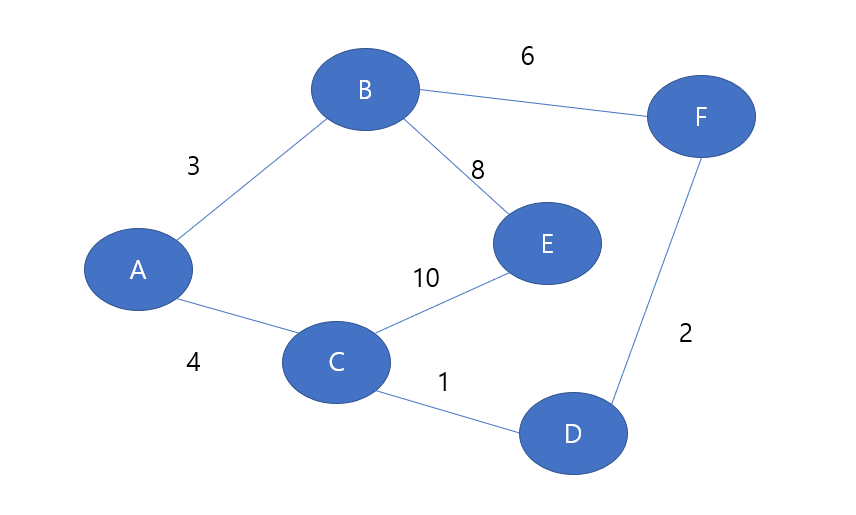
다음의 그래프와 배열이 있다고 하자, dist 배열은 처음에는 INF 값, 즉 엄청 큰 값을 저장해놓는다. 이는 위에서 나오는 다익스트라의 원리 중 하나인 최단 거리를 새로 갱신한다는 특성을 이용하려는 것인데, 다익스트라는 내가 이전까지 알고있던 최단 거리보다 더 짧은 최단 거리가 계산된다면 이 값으로 최단 거리를 새로 갱신한다. 따라서, 맨 처음부터 INF(절대 안나오는 값 또는 엄청 큰 값)으로 dist배열을 초기화해놓으면 처음부터 최단 거리를 새로 갱신할 수 있기 때문이다.

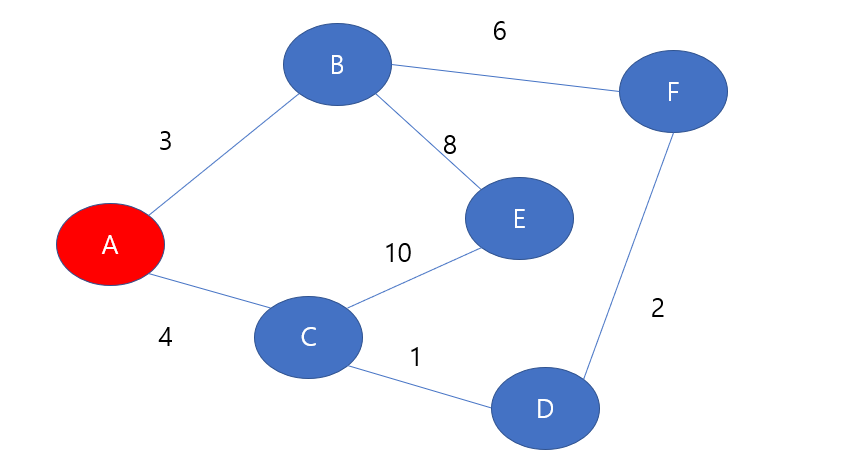
시작 노드를 A로 두자, A에서부터 시작하였으므로 dist배열의 A번째는 0으로 갱신해준다. check배열 또한 true로 바꾸어준다.

이제 앞에서 정리한 다익스트라의 원리를 다시보도록 하자,

시작 노드에서부터, 현재 내가 알고있는 모든 간선을 살펴보고 최단 거리를 갱신한다. 이후, 현재 내가 알고있는 거리 중에 최단 거리를 뽑고 해당 노드를 방문한다.

시작 노드인 A에서부터 현재 내가 알고있는 간선을 찾는다. 내가 알고있는 간선은 A-B와 A-C이다. 이 두 간선을 모두 방문하여 B와 C노드의 최단 거리를 갱신한다.

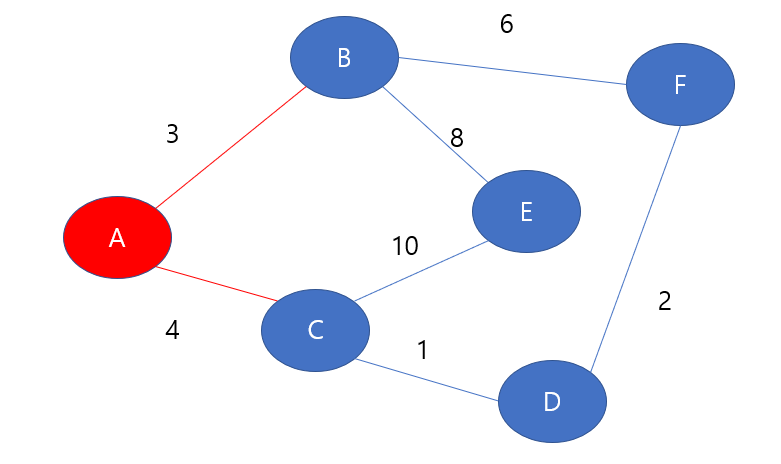
바로 다음과 같이 정리가 된다. dist배열의 B , C 노드의 최단 거리가 3 ,4 로 갱신된다. 다음으로 이들의 간선 가중치는 3, 4이므로 내가 현재 알고있는 최단 거리 중에 가장 최선의 최단 거리는 바로 3이기 때문에 A-B 간선을 선택하여 B노드를 방문한다.

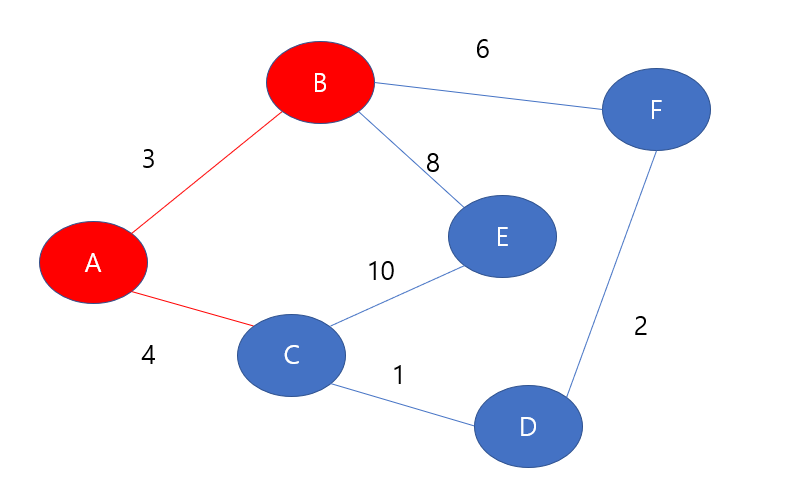
다음과 같이 B노드를 방문해준다. check배열은 B노드를 방문하였기 때문에 TRUE로 갱신해준다. 이제 위에서 정리한 원리 단계를 반복해주면 된다. 현재 내가 알고 있는 간선은 무엇이 있는가??

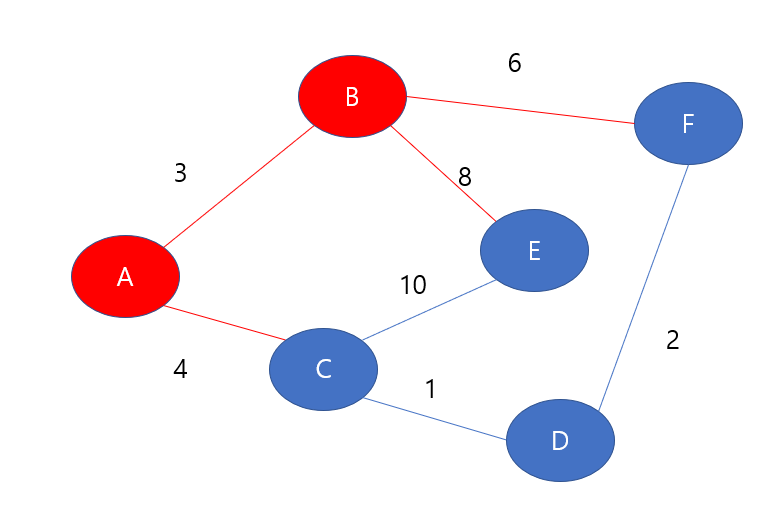
A-C, B-E, B-F 이렇게 3개의 간선이 존재하게 된다. 왜냐하면 나는 A와 B노드를 방문하였고, 이들과 연결된 간선은 A-B, A-C, B-E, B-F이기 때문이다. A-B는 이미 선택하였으므로 제외하면 나머지 3개이다.

따라서, 현재 내가 알고있는 간선들을 이용하여 이웃한 노드들의 최단 거리를 갱신한다. 주의해야할 것은 현재 내가 알고있는 간선들을 이용하여 최단거리를 갱신하는 것은 최선의 최단 거리가 아닐 수 있다는 것이다. 왜냐하면 '현재 내가 알고있는' 것일 뿐이기 때문이다.

E노드와 F노드의 최단 거리를 갱신해주는데, 주의해야할 것은 다익스트라는 시작 노드에서부터 임의의 노드까지의 최단 거리를 갱신하는 알고리즘이다. 따라서, B-E, B-F간선의 값이 각각 8, 6이라도, 시작 노드인 A-B 까지의 거리도 더해주어야 최단 거리가 된다.

즉, 시작 노드인 A에서 B까지의 최단거리 + B-E 간선의 가중치 = 시작 노드에서부터 E까지의 현재 최단 거리
시작 노드인 A에서 B까지의 최단거리 + B-F 간선의 가중치 = 시작 노드에서부터 F까지의 현재 최단거리

인 것이다.

따라서 dist배열의 E노드는 3+8 = 11
dist배열의 F노드는 3 + 6 = 9

가 된다.

이제 우리가 알고있는 최단 거리 중에 가장 짧은 것은 무엇인가?? 바로 dist 4값을 가지고 아직 방문하지도 않은 C노드이다.

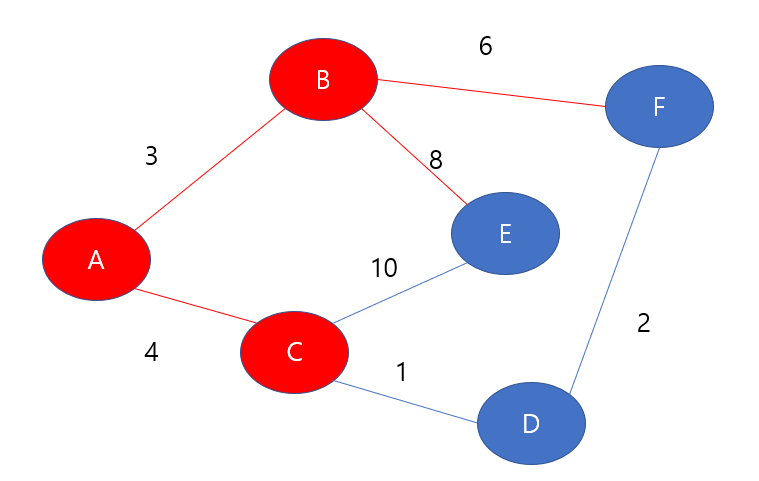
C노드를 방문하였으므로 check해주도록 하자, check 배열의 C노드를 true로 바꾸어주도록 하자.
이 다음, C노드와 연결된 간선을 통해 내가 현재까지 알고있던 최단 거리를 갱신해준다. 즉, 현재 알고있던 사실을 확장해나가는 것이다.

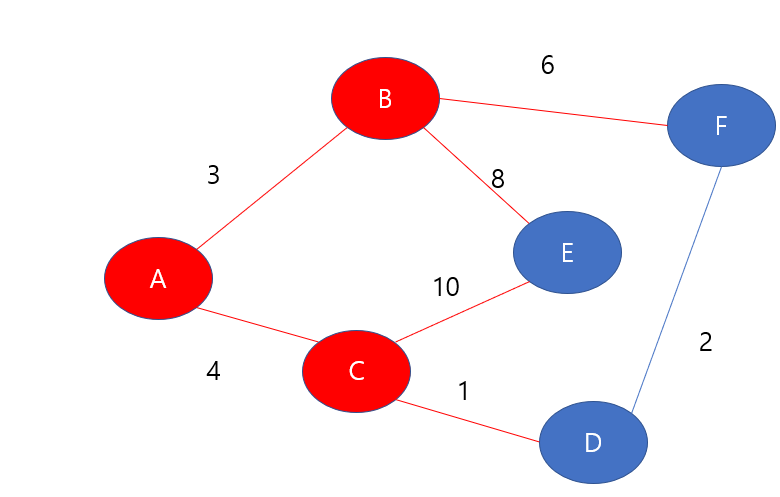
C노드와 연결된 간선인 C-E의 가중치는 10이고 C-D의 가중치는 1이다. D노드는 이전에 INF값이었으므로, 최단 거리가 갱신이 된다.

현재까지의 D노드 최단 거리 = C노드의 최단 거리 + C-D 간선의 가중치

5 가 되므로 위의 사진에서 dist배열의 D노드가 5로 갱신된 것을 확인할 수 있다.

그럼 다음 간선인 C-E 간선을 보도록 하자 E노드의 최단 거리가 현재까지는 11이었다.
새롭게 알게된 E노드의 거리 = C노드의 최단거리 + C-E간선의 가중치 = 14 가 된다.

그럼 현재까지의 E노드의 최단 거리보다 크다는 것을 알 수 있으므로, 우리는 E노드의 최단 거리를 갱신할 필요가 없다는 사실을 알게된다. 따라서 갱신해주지 않는다.

여기서 우리가 생각해볼 점이 하나 있다.
현재까지의 D노드 최단 거리 = C노드의 최단 거리 + C-D 간선의 가중치 에서 C노드의 최단 거리가 과연 보장이 되냐는 것이다.

즉, 시작 노드에서 C노드까지의 최단 거리가 현재 내가 알고있는 정보를 이용하여 갱신한 최단거리인데, 이게 과연 전체의 최단 간선을 고려하여 계산한 C노드의 최단 거리와 일치하냐는 것이다.

정답은 최단 거리가 맞다. 왜냐하면 우리가 방문하는 노드들은 우리가 알고있는 최단 거리 중에 가장 적은 최단 거리 값을 뽑아내어 노드를 방문해주었기 때문이다. 방문한 노드, 즉, check된 노드들은 시작 노드에서부터 가장 적은 최단 거리를 가지는 값들이다. 즉, 방문하지않고 최단 거리를 갱신만해준 노드들은 현재까지의 거리가 최선의 최단 거리라는 것이 보장되지 않는다. 그러나, 방문한 노드들은 시작 노드에서부터 가장 짧은 최단 거리로 이동한 것이기 때문에, 방문한 노드들의 거리는 최단 거리라는 것이 보장된다.

따라서 D노드의 최단 거리를 C노드까지의 최단 거리를 이용하여 갱신할 수 있는 것이다.

이제 방문하지도 않았고, 우리가 알고있는 최단 거리 중에서 가장 짧은 거리를 갖는 노드를 찾아 방문해주도록 하자. D노드가 가장 작은 최단 거리 값을 가지고 있고, 아직 방문하지도 않았으므로 D노드를 선택해준다.

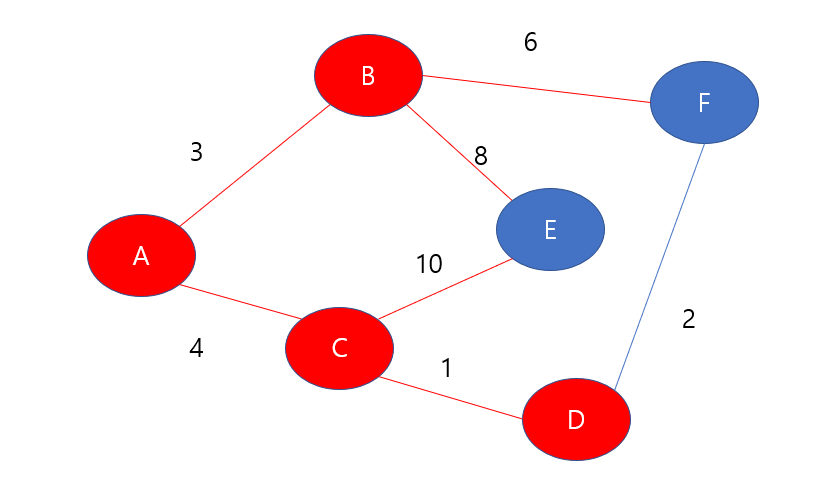
D노드를 방문하였기 때문에 check배열을 갱신해준다.
그럼, D노드가 새롭게 알게된 사실이므로, D노드와 연결된 간선들을 이용하여 최단 거리를 갱신해보도록하자

D노드와 연결된 간선은 D-F이다. 해당 간선의 가중치가 2이므로 D까지의 최단 거리를 이용하여 F까지의 최단 거리를 계산해보자

D까지의 최단거리 (5) + D-F간선의 가중치(2) = 7이다.
기존의 F노드의 최단 거리는 9이므로, D를 경유하여 F노드로 가는 것이 더 좋은 최단 거리임을 알 수있다. 따라서 갱신해주도록 하자

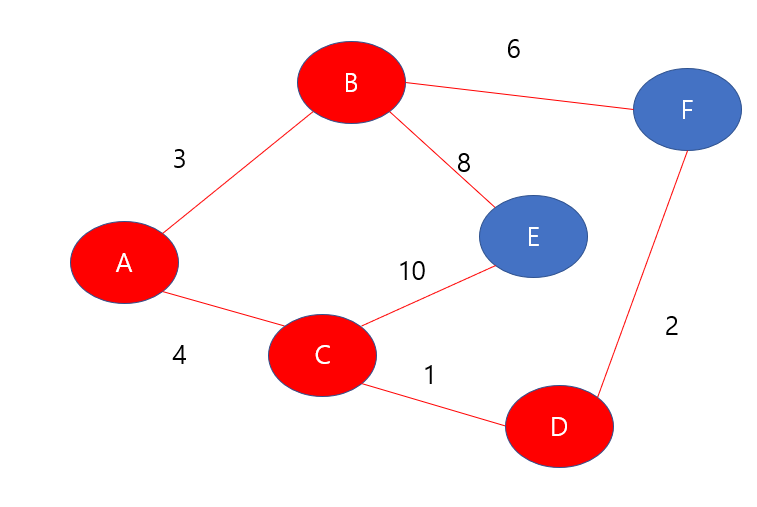
다음으로 가장 적은 거리를 가진 노드를 선택해보도록 하자, 방문하지않은 노드는 E와 F인데, E는 11, F는 7이다. F의 값이 더 작으므로 F를 방문하도록 한다.

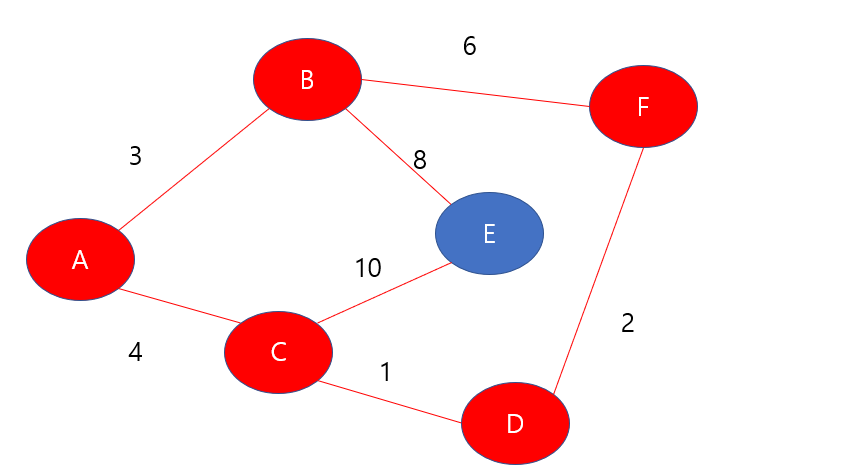
F노드를 방문하였으므로 check해주도록 하자, 그 다음 F노드와 연결된 간선을 확인하여 최단 거리를 갱신주도록 하자, F와 연결된 간선은 이미 고려되었기 때문에 굳이 확인해줄 필요가 없다.

따라서, 마지막 노드인 E노드를 방문하여 다익스트라 알고리즘을 완료하면 된다.

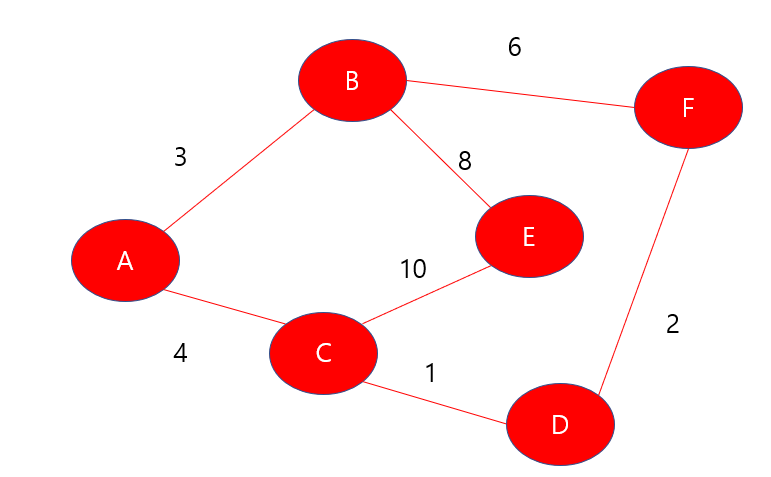
이것이 우리가 최종적으로 얻은 최단 거리인 것이다.

다시 원리 부분을 되새겨보자,

시작 노드에서부터, 현재 내가 알고있는 모든 간선을 살펴보고 최단 거리를 갱신한다. 이후, 현재 내가 알고있는 거리 중에 최단 거리를 뽑고 해당 노드를 방문한다. 이렇게 모든 간선을 한 번 이상 방문하여, 현재 내가 알고있는 특정 노드까지의 거리가 최소가 되도록 바꾸는 것이다.

정리하자면, 다익스트라는 시작 노드에서 임의의 노드까지의 최단 거리를 구하는 알고리즘으로 현재 노드에서 알 수 있는 최단 거리를 모두 갱신한 다음, 방문하지않은 노드 중 가장 적은 최단 거리로 갈 수 있는 노드를 방문하도록 한다는 것이다.

시작 노드에서부터 최단 거리로 노드를 방문하다보면, 방문한 노드는 최단 거리가 된다. 이 노드의 최단 거리가 밝혀졌으니 이를 이용하여 다음 노드를 탐색하여 최단 거리를 계산하면 되는 것이다.

2. 다익스트라의 구현(stl)

그런데, 문제가 있다.
우리는 방문하지않은 노드 중에 최단 거리를 가지는 노드를 뽑아내었는데, 이걸 어떻게할 것이냐는 것이다.

만약, 아주 원시적으로 하자면 브루트 포스로 탐색이 가능하다. 즉, 모든 dist배열들을 순회하는 것이다. 그렇다면, 간선 수만큼 순회를 하기 때문에 O(간선*dist 배열의 크기) 가 된다.

여기서 노드의 개수를 V라고 하고, 간선의 개수를 E라고 하자, 위의 시간 복잡도는 O(E*V) 가 되는 것인데, 간선 E는 최소의 값이 V-1이다. 따라서, O(V(V-1))이 되고, O(v^2)이 된다.

이것이 문제가 무엇이냐면, 시작 노드에서 모든 노드의 최단 거리를 구하는 최단 거리 알고리즘의 브루트 포스는 사실 O(V^2)만큼 순회하면 쉽게 구할 수 있다. 즉, V개의 노드에서 한 개를 목적지로 설정하고 시작 노드를 포함한 나머지 V-1개의 노드를 모두 순회하여 간선들을 따라 최단 거리를 갱신해주면 된다.

그러면 다익스트라 알고리즘이 의미가 없어지는 것이다. 그래서 우리는 방문하지 않는 노드 중에 최단 거리를 가지는 노드를 뽑기위해서 최소힙을 이용할 것이다.

최소힙을 이용하면 O(logn) 시간 안에 최단 거리를 가지는 노드를 찾아낼 수 있다. 따라서 모든 간선을 순회하는 동안 최소힙에서 최단 거리를 가지는 노드를 뽑아내므로 시간 복잡도는 O(ElogV) 가 된다.

그러기 위해서 우리가 최소힙을 구현해야하는데, 이는 여간 복잡한 일이 아니다.

그러나, 우리의 희망 stl이 있으니!! 이것을 이용하면 된다.

#include <queue>
priority_queue<int, vector<int> , greater<int>> pq;

이전에 최소힙, 최대힙을 할 때 배웠던 priority_queue이다. 위는 최소힙을 구현한 것이다.

#include <queue>
priority_queue<int> pq;

만약 priority_queue에 어떠한 설정값을 넣어주지 않으면 이는 최대힙이다. 즉, 가장 큰 값이 맨 앞으로 온다.

최소힙을 만들어주기 위해서는 greater<자료형> 을 3번째 인자에 넣어주어야한다. 왜 최소힙인데 greater냐?? greater는 더 큰 값이 앞으로 오는 거 아니냐? 라고 할 수 있다.

이는 priority_queue 내부를 찾아보면 된다. ~~이거 내부 들여다보는 변태가 어딨냐~~
priority_queue 내부 구현에 기본 컨테이너로 vector가 사용된다. 따라서 최소힙을 만들 때 두 번째 인자로 vector<> 를 넣어주는 것이다.

vector로 구현된 힙은 맨 앞, 즉 인덱스 0 번째에 root(가장 작거나, 큰 값)을 넣어주지 않고, 맨 마지막 칸에 root값을 넣는다. 왜냐하면 vector는 동적으로 사이즈가 변화하는 배열로 맨 앞에 값을 넣어주어 계속 바꾸어주기 보다는 맨 뒤에 값을 변경하는 것이 더 속도가 빠르기 때문이다.

따라서, priority_queue의 root값이 맨 뒤에 있으므로 최소힙을 만들기 위해서는 greater을 써야하는 것이다.

priority_queue<자료형, 컨테이너, 비교함수> pq;

priority_queue의 설정값을 정리하면 다음과 값다. 최대힙이면 첫번째 인자인 자료형만 써주면 된다.

~~어차피 최소힙 짜는 것보다 훨씬 쉬우니까 외우도록 하자~~

그럼 구현의 과정을 나열해보도록 하겠다.

1. dist는 INF(문제에서 절대 나올 수 없는 큰 값)값, check는 false로 초기화, 최소힙 준비
2. 시작 노드에서부터 출발하기 때문에 시작 노드의  dist값은 0, 최소힙에 (0, 시작노드)를 넣는다.
3. 최소힙에서 현재 알고있는 최단 거리 중에 가장 작은 값을 가지는 것을 꺼낸다. 만약 해당 노드를 이미 방문했다면 무시하고, 다시 3번 과정을 반복한다.
4. 해당 노드를 방문하기 때문에 check배열에 true를 넣어주고, 연결된 간선을 모두 순회하여 이웃한 노드의 최단 거리를 갱신한다.
5. 갱신된 최단 거리를 최소힙에 넣어준다. (최단 거리, 노드)로 넣는다.
6. 다시 3번으로 돌아간다. 만약, 3번 과정에서 더 이상 최소힙에서 꺼낼 원소가 없다면 종료한다.

그럼 이제 구현을 해보자

#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
#include <cstring>
using namespace std;

priority_queue<pair<int,int> , vector<pair<int,int>> , greater<pair<int,int>>> pq;
vector<pair<int,int>> arr[10];
bool check[10];
int dist[10];
int main(){
    //from , dist, to
    arr[1].push_back(make_pair(3,2));
    arr[1].push_back(make_pair(4,3));
    arr[2].push_back(make_pair(3,1));
    arr[2].push_back(make_pair(8,5));
    arr[2].push_back(make_pair(6,6));
    arr[3].push_back(make_pair(4,1));
    arr[3].push_back(make_pair(1,4));
    arr[3].push_back(make_pair(10,5));
    arr[4].push_back(make_pair(1,3));
    arr[4].push_back(make_pair(2,6));
    arr[5].push_back(make_pair(8,2));
    arr[5].push_back(make_pair(10,3));
    arr[6].push_back(make_pair(6,2));
    arr[6].push_back(make_pair(2,4));
    
    //초기화
    int n = 6;
    memset(dist, 127, sizeof(dist));
    memset(check,false,sizeof(check));
    //시작 노드
    int start = 1;
    dist[start] = 0;
    pq.push(make_pair(0,start));
    while(!pq.empty()){
        pair<int,int> cur = pq.top();
        pq.pop();
        int curNode = cur.second;
        int curDist = cur.first;
        if(check[curNode]) continue;
        check[curNode] = true;
        for(int i = 0; i < arr[curNode].size(); i++){
            int nextNode = arr[curNode][i].second;
            int nextDist = arr[curNode][i].first;
            if(dist[nextNode] > dist[curNode] + nextDist){
                dist[nextNode] = dist[curNode] + nextDist;
                pq.push(make_pair(dist[nextNode], nextNode));
            }
        }
    }
    for(int i = 1; i <= n; i++){
        cout << start << "노드에서 " << i << "번째 노드까지의 최단 거리는 " << dist[i] << " 입니다." << '\n';
    }
}

결과

1노드에서 1번째 노드까지의 최단 거리는 0 입니다.
1노드에서 2번째 노드까지의 최단 거리는 3 입니다.
1노드에서 3번째 노드까지의 최단 거리는 4 입니다.
1노드에서 4번째 노드까지의 최단 거리는 5 입니다.
1노드에서 5번째 노드까지의 최단 거리는 11 입니다.
1노드에서 6번째 노드까지의 최단 거리는 7 입니다.

위의 예제 A, B ,C ,D ,E ,F를 1 ,2 ,3 ,4 ,5 ,6으로 바꾸어 계산한 것이다.

구현 부분을 상세히보면 다음과 같다.

priority_queue<pair<int,int> , vector<pair<int,int>> , greater<pair<int,int>>> pq;
vector<pair<int,int>> arr[10];
bool check[10];
int dist[10];

먼저 필요한 자료구조들을 선언한다. 여기서 arr는 인접리스트이다. arr와 check,dist 모두 node의 개수에 비례하므로 이에 유의하여 사이즈를 선언하면 된다.

    //from , dist, to
    arr[1].push_back(make_pair(3,2));
    arr[1].push_back(make_pair(4,3));
    arr[2].push_back(make_pair(3,1));
    arr[2].push_back(make_pair(8,5));
    arr[2].push_back(make_pair(6,6));
    arr[3].push_back(make_pair(4,1));
    arr[3].push_back(make_pair(1,4));
    arr[3].push_back(make_pair(10,5));
    arr[4].push_back(make_pair(1,3));
    arr[4].push_back(make_pair(2,6));
    arr[5].push_back(make_pair(8,2));
    arr[5].push_back(make_pair(10,3));
    arr[6].push_back(make_pair(6,2));
    arr[6].push_back(make_pair(2,4));

값들을 설정해주는데, arr는 인접리스트이므로 여기에 값을 넣어준다. 그런데 이전에 했던 것처럼 pair에는 (to, dist) 순서가 아니다. 즉, 간선을 저장하는 방식이 다음과 같다.

arr[시작].push_back(make_pair(최단 거리, 목적지));

이다.

왜 이런 순서로 저장하냐면 최소힙인 pq때문인데, 최소힙을 구현하기위해 사용한 greater비교 함수는 자신이 가진 자료형의 맨 처음 값을 먼저 비교하고, 같은 경우 다음 값을 비교한다. 따라서 우리가 원하는 것은 가장 작은 최단 거리이므로 (최단 거리, 목적지) 순서로 저장하는 것이다.

int n = 6;
memset(dist, 127, sizeof(dist));
memset(check,false,sizeof(check));

초기화 부분이다. memset을 사용하면 쉽게 초기화되는데, 가운데에 있는 값으로 배열의 size만큼 초기화해준다. 가운데 크기를 127로 써주면 int의 가장 큰 값까지 초기화되므로 이를 이용해주면 된다.

    int start = 1;
    dist[start] = 0;
    pq.push(make_pair(0,start));
    while(!pq.empty()){
        pair<int,int> cur = pq.top();
        pq.pop();
        int curNode = cur.second;
        int curDist = cur.first;
        if(check[curNode]) continue;
        check[curNode] = true;
        for(int i = 0; i < arr[curNode].size(); i++){
            int nextNode = arr[curNode][i].second;
            int nextDist = arr[curNode][i].first;
            if(dist[nextNode] > dist[curNode] + nextDist){
                dist[nextNode] = dist[curNode] + nextDist;
                pq.push(make_pair(dist[nextNode], nextNode));
            }
        }
    }

다익스트라 부분인데, BFS랑 별반 다를바가 없어보인다. 시작 노드에서 dist를 1로 초기화하고 최소힙인 pq에 넣어준다. 그 다음 pq가 비어있지 않을 때까지 반복해주고, pq에서 현재 최단 거리 중에 가장 작은 값을 가진 pair를 가져온다.

해당 pair로 curNode와 curDist를 가져오고 check배열에서 curNode가 이미 순회하였다면, 방문해주지 않고, 방문하지 않았다면 check배열에 true로 바꾸어준다.

이 다음은 BFS에서 연결 리스트 그래프의 순회와 같다. 연결된 간선들을 모두 순회하여 현재 목적지 노드(nextNode)의 dist 값보다, 새로 구한 값이 더 작다면 이를 갱신해주도록 한다.

주의!!

BFS할 때 처럼 pq, 즉 최소힙에 넣기 전에 check를 먼저해주면 안된다.
BFS는 큐에 넣어줄 때 check해야 다음 노드가 또 방문하지 않는다. 이는 시간복잡도를 위해 해주어야하는 연산이다. 즉, N개의 노드가 있고, N개의 노드 모두 서로 연결되어 각각이 N-1개의 간선으로 이루어져있다면, 이는 중복해서 노드를 큐에 넣는 경우 O(N^2) 시간이 걸리기 때문이다.

그러나, 다익스트라는 어차피 시간 복잡도가 O(VlogN)이기 때문에 어차피 간선의 개수가 많아지면 값이 더 커질 수 밖에 없다. 그렇기 때문에 큐에 넣기전에 check를 할 필요가 없다.

이런 이유도 있지만, 더 큰 이유가 있다. 다음의 경우를 보도록 하자

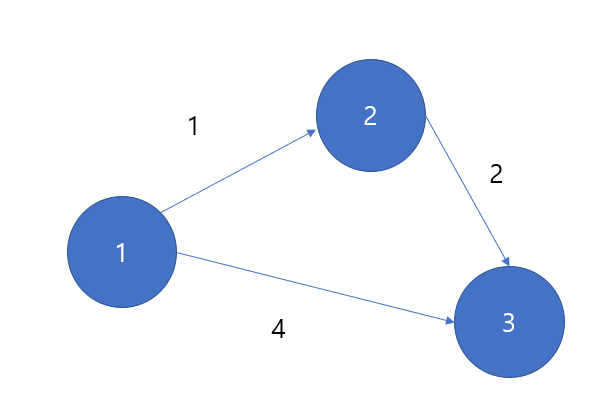
다음의 그래프가 있다고 하자, 우리는 1번 노드를 시작으로 2,3번 노드의 최단거리를 구하려고한다.

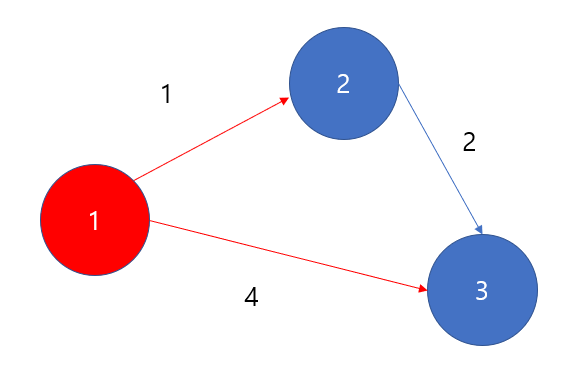
1번 노드를 방문하였의니 check해주고 (최단 거리, 목적지) 로 최소힙에 넣어주도록하자
(1,2)와 (4,3)을 넣을 수 있을 것이다.

pq(최소힙) : (1,2) ,(4,3)

이 될 것이고, dist[2] = 1, dist[3] =4로 갱신된다.
pq에서 다음 노드를 빼내주면 (1,2)가 나올 것이고, 2번 노드를 방문해준다.

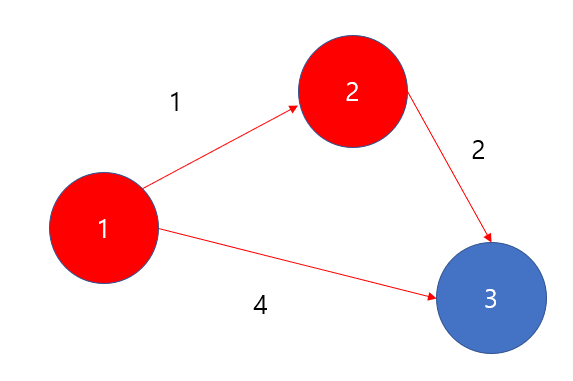
다음과 같이 2번 노드를 방문하고, 2번 노드와 연결된 간선으로 3번 노드의 최단 거리를 계산해주면, (3,3) 이 될 것이고, 이는 dist[3] =4보다 작으므로 pq에 넣어줄 수 있다.

pq(최소힙) : (3,3) , (4,3)

이 된다.

바로 여기가 중요한 것이다. pq(최소힙)안에 있는 값들을 잘보면 같은 노드지만 다른 최단 거리를 가지고 있는 것을 볼 수 있다. 이는 이전에 계산했던 해당 노드의 최단 거리가, 실제 최단 거리가 아님을 의미하는 것이다.

따라서, 탐색을 진행하면서 더 많은 경로를 알게되고 더 짧은 최단 거리가 나오게되면서 업데이트해주어야 하는 것이다. 이를 위해 check를 pq(최소힙)에 넣어줄 때 하는 것이 아니라, 실제로 pq(최소힙)에서 꺼내줄 때 check를 해주는 것이다.

check를 해주었다는 것은 pq에서 해당 노드가 처음으로 나왔다는 것을 의미하고, 이에 따라 해당 노드와 연결된 간선을 확인하겠다는 것이다. 또한 check되었다는 것은 이제 해당 노드의 최단 거리는 더 이상 업데이트되지 않는다는 것을 의미한다.

왜냐하면 check된 노드에 대해서 또 다른 경로로 최단 경로가 존재한다면, 우리는 이전에 이미 해당 경로를 방문했을 것이다. 왜냐하면 우리는 가장 작은 최단 경로를 먼저 방문해왔기 때문이다. 그런데, check된 노드에 대해서 또 다른 최단 경로가 존재한다는 것은 모순이기 때문이다.

더 간단한 그림의 예를 보면 다음과 같다.

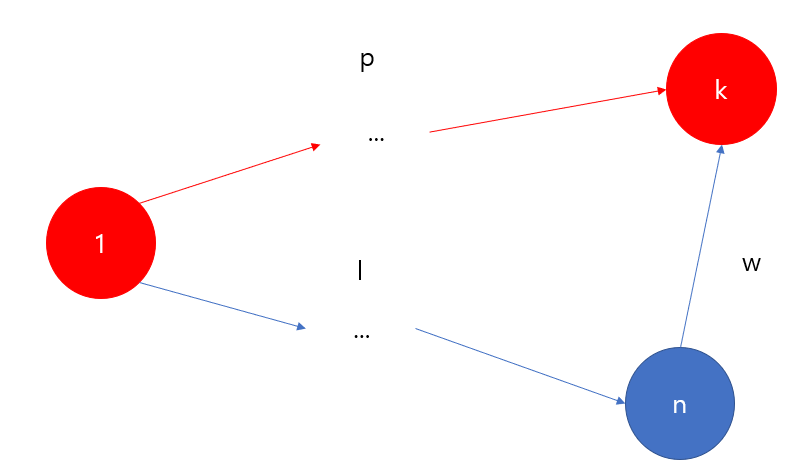
1번 시작 노드에서 k로 가는 경로가 빨간색으로 표시되어있다고 하자, 우리는 1~k까지가는 최단 거리를 p라고 정의하자

1~k까지갔고, k를 check했지만 1~n->k 로 가는 것이 사실 최단 거리라고 하자
그럼 두 가지 경우가 있다.

1. p보다 l이 더 작고, l+w이 더 작다.
  이는 말이 안된다. p보다 l이 더 작았다면 l을 따라갔을 것이다. 왜냐하면 우리는 현재 자신이 알고있는 거리 중 최단 거리로만 이동했기 때문이다.
1. p보다 l이 더 크고, l+w이 더 작다.
  이 역시도 말이 안된다. 그렇다면 우리가 이미 p로 가기 전에 l+w로 이동했을 것이기 때문이다.

이것이 가능한 이유는 다익스트라는 각 노드의 간선의 최소값을 선택하는 것이 아닌, 최단 거리를 선택하는 것이기 때문이다. 즉, 이전까지의 현재 노드를 오는데 까지 필요한 거리를 합산해서 연결된 가중치와 계산하기 때문이다.

그렇기 때문에 pq(최소힙)에서 빼낼 때가 해당 노드의 최단 거리가 되며, check를 해줄 수 있는 이유인 것이고, check가 곧 해당 노드의 최단 거리를 찾았다는 의미가 된다.

3. 다익스트라 (쌩구현)

그냥 stl로만 구현하면 재미가 없다.
그래프, 최소힙부터 모두 다 구현해보자

#include <iostream>
#define MAX_NODE_SIZE 100
#define MAX_EDGE_SIZE 100
#define MAX_HEAP_SIZE 100
#define INF 1e9
using namespace std;

typedef struct Node{
    int end;
    int weight;
    Node *next;
    Node(){
        next = 0;
    }
    Node(int end, int weight) : end(end), weight(weight){}
    bool operator<(const Node &second){
        return weight <= second.weight;
    }
    void push_back(int weight, int dest);
};

Node pool[MAX_EDGE_SIZE*2+10];
int pi = 0;
Node graph[MAX_NODE_SIZE+10];

Node *aloc(int e, int t){
    pool[pi].end =e;
    pool[pi].weight = t;
    pool[pi].next = 0;
    return &pool[pi++];
}

void Node::push_back(int weight, int dest){
    Node* newNode = aloc(dest, weight);
    newNode->next = next;
    next = newNode;
}

bool check[MAX_NODE_SIZE+ 10];
int dist[MAX_NODE_SIZE + 10];
int n , m ,x;

Node heap[MAX_HEAP_SIZE+10];
int hi = 1;

void upHeapify(int index){
    int parent = index/2;
    while(parent > 0){
        if(heap[parent] < heap[index]) return;
        Node temp = heap[index];
        heap[index] = heap[parent];
        heap[parent] = temp;
        index = parent;
        parent = index/2;
    }
}

void downHeapify(int index){
    int left = index*2;
    while(left <= hi-1){
        if(left + 1 <= hi-1){
            if(heap[left+1] < heap[left]) left++;
        }
        if(heap[index] < heap[left]) return;
        Node temp = heap[left];
        heap[left] = heap[index];
        heap[index] = temp;
        index = left;
        left = index*2;
    }
}

void addHeap(int end, int weight){
    heap[hi].end = end;
    heap[hi].weight = weight;
    upHeapify(hi);
    hi++;
}

Node popHeap(){
    Node temp = heap[1];
    heap[1] = heap[hi-1];
    hi--;
    downHeapify(1);
    return temp;
}

void init(int n){
    for(int i = 0; i <= n; i++){
        dist[i] = INF;
        check[i] = false;
        graph[i].next = 0;
    }
    hi = 1;
    pi = 0;
}

int main(){
    n = 6;
    init(n);
    graph[1].push_back(3,2);
    graph[1].push_back(4,3);
    graph[2].push_back(3,1);
    graph[2].push_back(8,5);
    graph[2].push_back(6,6);
    graph[3].push_back(4,1);
    graph[3].push_back(1,4);
    graph[3].push_back(10,5);
    graph[4].push_back(1,3);
    graph[4].push_back(2,6);
    graph[5].push_back(8,2);
    graph[5].push_back(10,3);
    graph[6].push_back(6,2);
    graph[6].push_back(2,4);
    dist[1] = 0;
    addHeap(1,0);
    while(hi != 1){
        Node now = popHeap();
        int start = now.end;
        int weight = now.weight;
        if(check[start]) continue;
        check[start] = true;
        for(Node *cur = graph[start].next; cur != 0; cur = cur->next){
            if(dist[cur->end] > dist[start] + cur->weight){
                dist[cur->end] = dist[start] + cur->weight;
                addHeap(cur->end, dist[cur->end]);
            }
        }
    }
    for(int i = 1; i <= n; i++){
        cout << 1 << "노드에서 " << i << "번째 노드까지의 최단 거리는 " << dist[i] << " 입니다." << '\n';
    }
    
}