
Heap Sort(힙 정렬)
1. 트리 구조(Tree Structure)
힙 정렬을 알아보기 전에 이진트리에 대해서 알아야한다.
1-1. 이진 트리(Binary Tree)
이진트리(Binary Tree)는 컴퓨터가 데이터를 표현할때, 데이터를 두개씩 이어붙이는 것을 말한다.
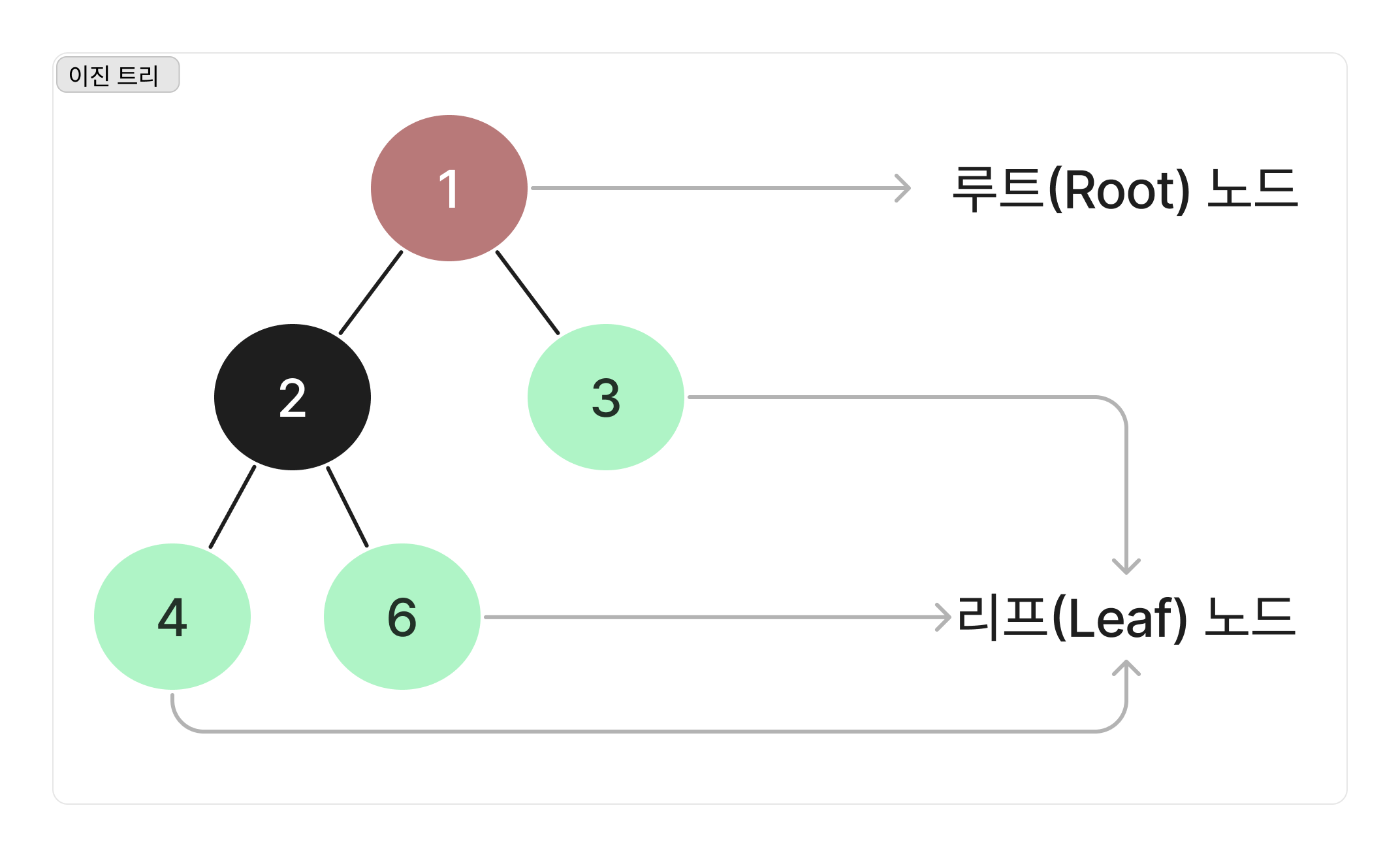
각 데이터는 노드라고 말한다.
가장 최상단에 홀로 위치하는 노드를 루트(Root) 노드,
가지의 끝 최 하단에 위치하는 노드들을 리프(Leaf) 노드라고한다.
가지를 뻗어 나가듯 데이터를 뻗어 나간다고해서 트리(Tree)라고 한다.
1-2. 완전 이진 트리(Complete Binary Tree)
완전 이진트리란, 이진 트리의 한 종류이다.
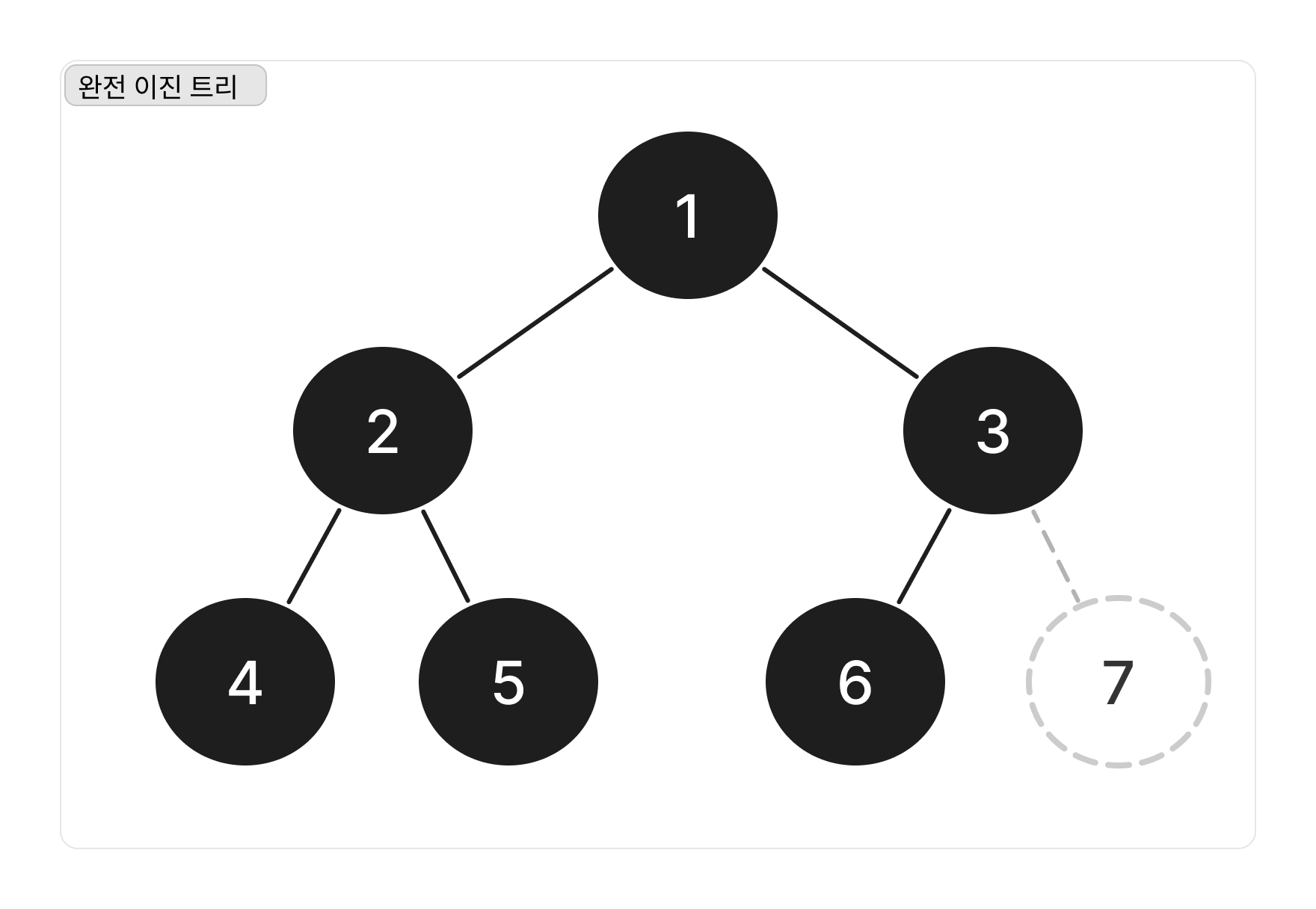
데이터가 루트(Root) 노드를 시작으로 자식 노드가 왼쪽부터 차례대로 들어가는 구조로 되어있다.
일반 이진트리의 경우 가지가 중간에 비어있을 수 있지만, 완전 이진트리의 경우에는 빽뺵히 차있다.
2. 힙(Heap)
힙(Heap)은 최댓값 혹은 최솟값을 빠르게 찾아내기 위해 완전 이진트리를 기반으로 하는 트리이다.
2-1. 최대힙과 최소힙
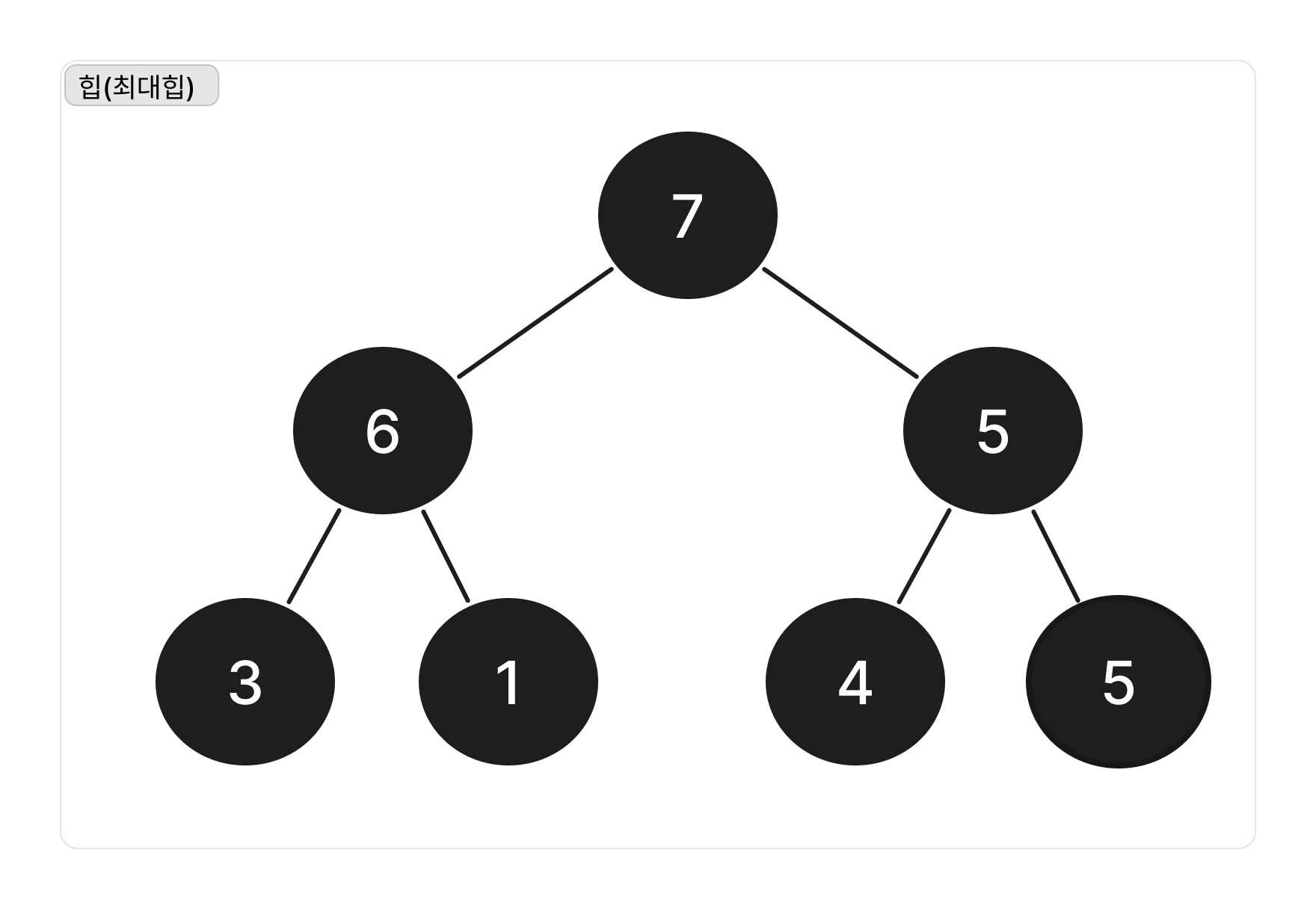
최대힙은 부모 노드가 자식 노드보다 큰 경우를 말한다.
자식 노드가 부모 노드보다 크다면 최대힙이라고 할 수 없다.
특정 노드로 인해 힙이 붕괴되는 겅우가 있다.
이때는 노드의 자식들 중 더 큰 값과 부모를 바꿔주면된다.
이를 힙 생성(Heapify) 알고리즘이라고 한다.
2-2. 힙 생성(Heapify) 알고리즘
이 알고리즘을 사용하면 힙 구조를 유지할 수 있다.
계속해서 힙을 유지할 수 있도록 자식 중에서 더 큰 값이 있다면 바꿔 줄 수 있도록 반복 수행한다.
이 힙 생성 알고리즘의 시간 복잡도는 O(log(n))을 따르게 된다.
내려갈 때마다 2로 나눠지면서 지수적으로 늘어나기 때문에
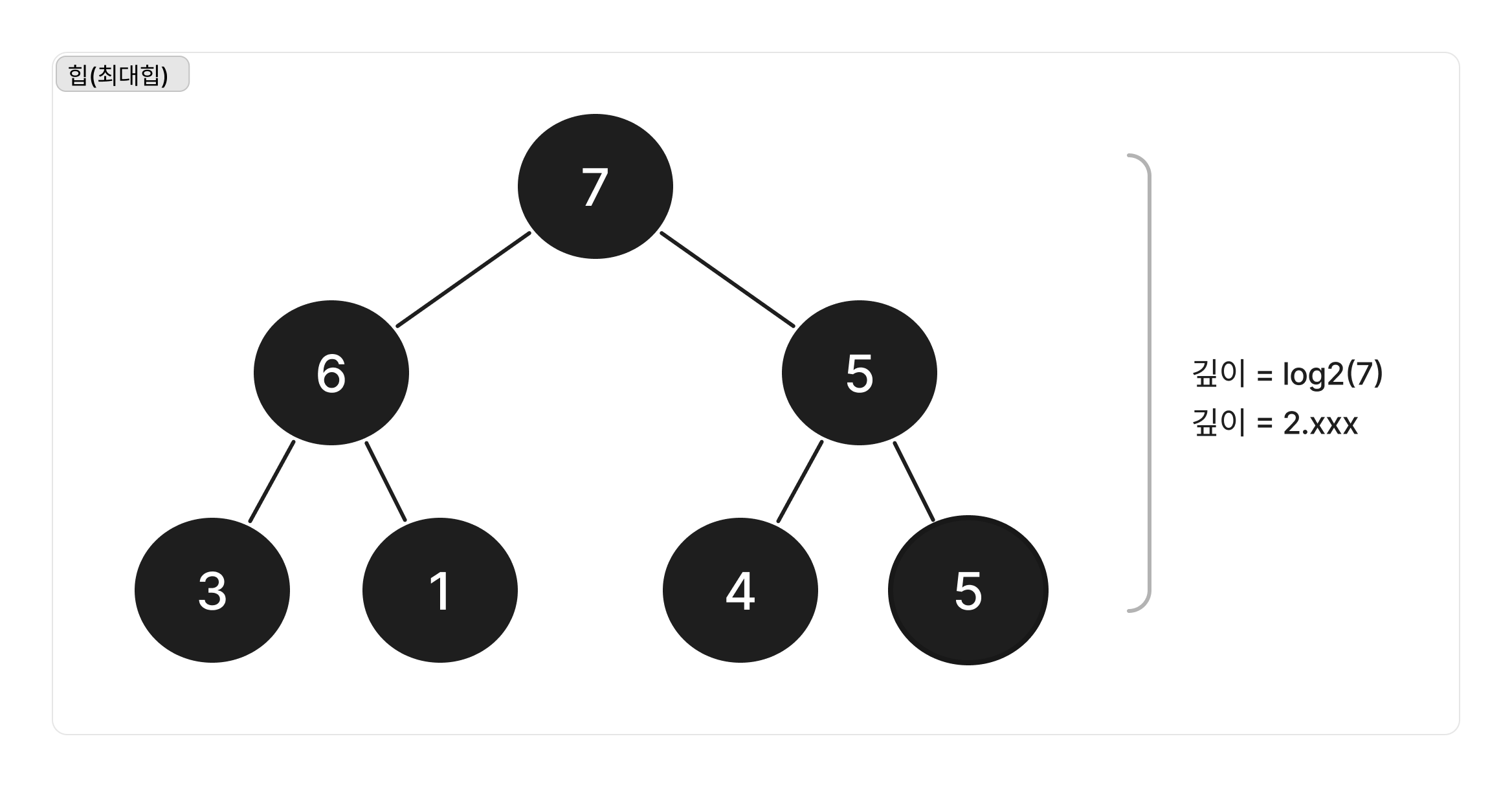
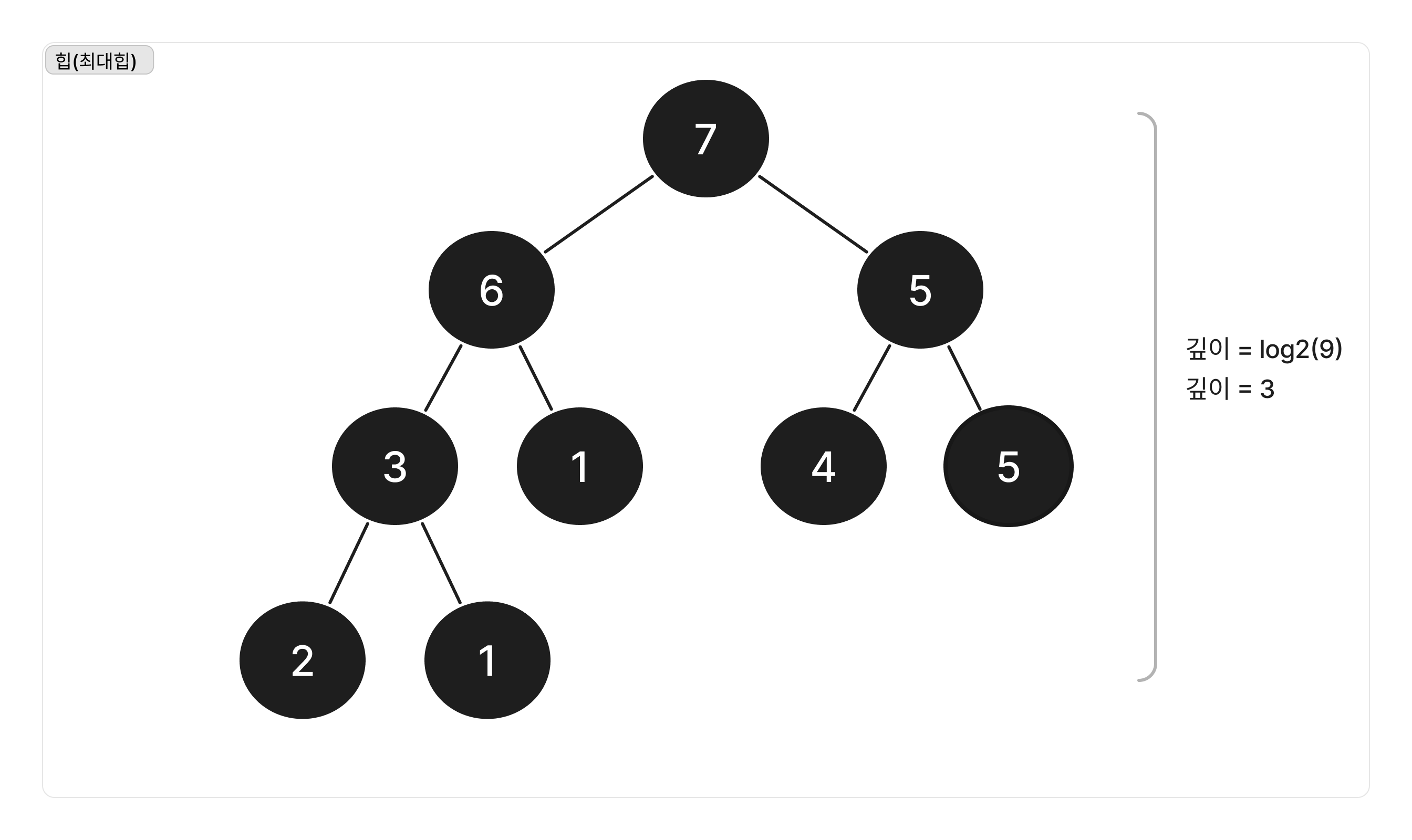
전체 N개의 노드에 밑이 2인 로그 log2를 씌우면 깊이를 알 수 있다.
힙의 생성에 있어서는 O(log n)의 시간 복잡도를 따른다고 할 수 있다.
전체 노드(N)에 대해 힙 생성 알고리즘을 적용해야 하므로 이 과정은 O(n)을 따르게 된다.
이 둘을 같이 사용하기 떄문에 곱하여 O(n log(n))를 따른다.
3. 힙 정렬(Heap Sort) 문제 풀기
다음을 정렬하라.
7 6 5 8 3 5 9 1 6
위 문제를 이진 트리로 표현해보면,
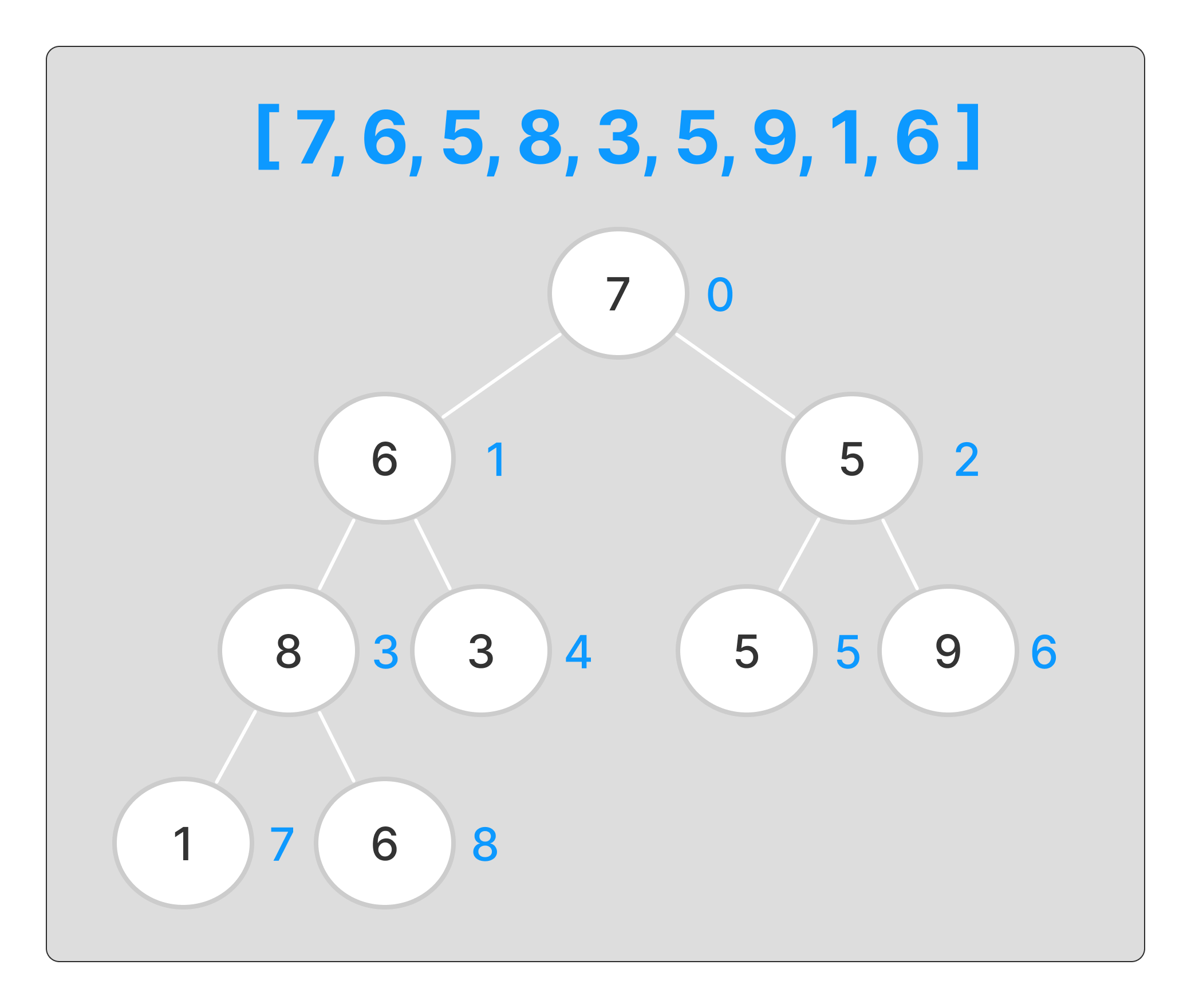
이렇게 표현이 가능한데, 이를 힙 정렬 알고리즘을 이용해서 정렬을 해보자.
한 노드의 묶음으로 시작해야한다.
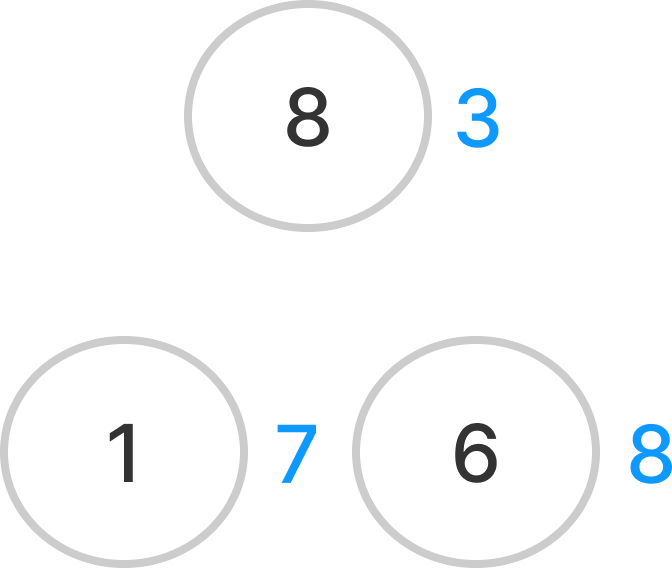
이런식으로 자식이 있는 노드들을 판별해야 한다.
이를 위해서는 노드의 길이를 절반으로 자르면,
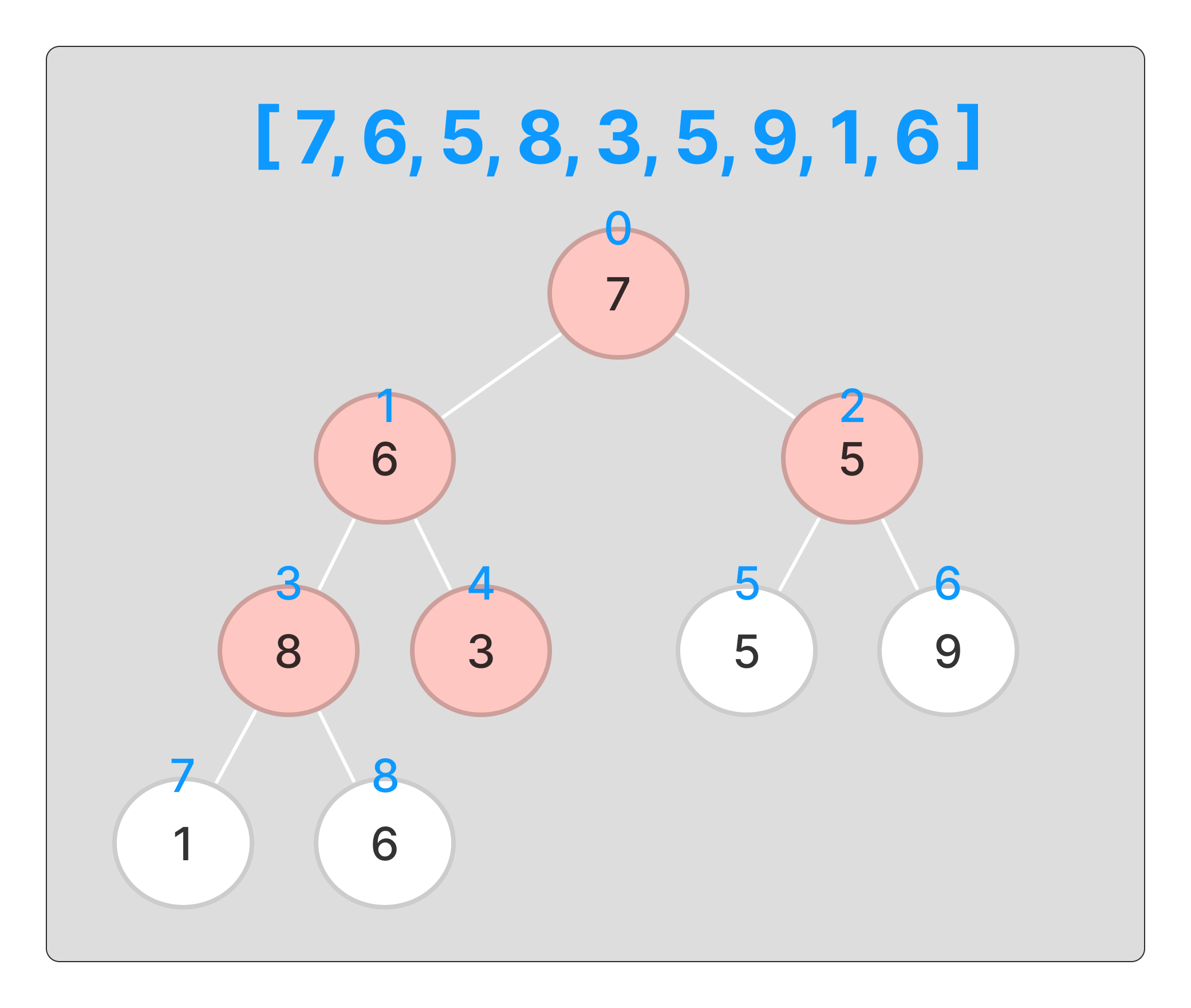
이렇게 자식 노드가 있을 가능성이 생긴다.
이 중에서 제일 높은 인덱스를 가진 것 부터 판별해 나간다.
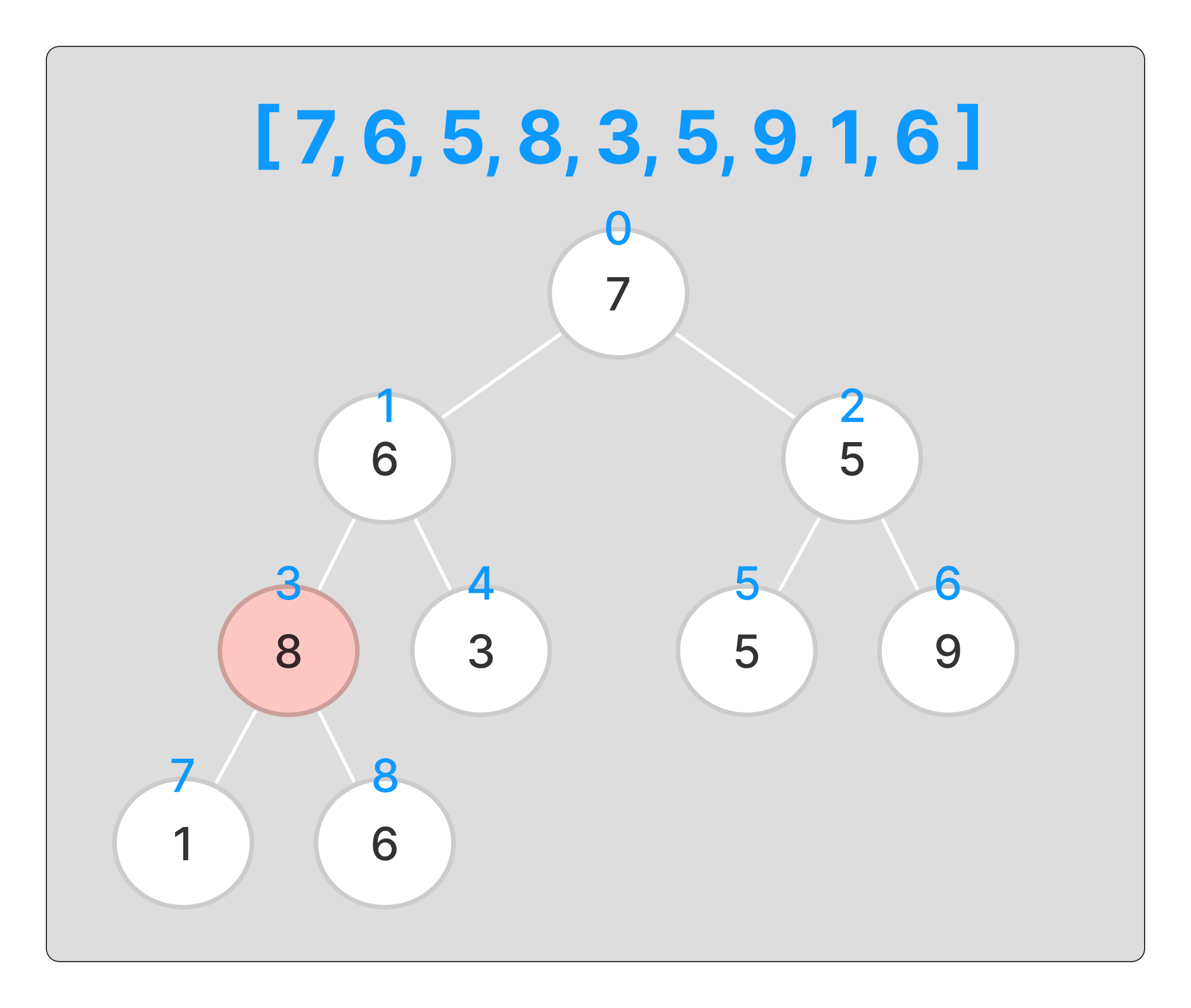
8은 최대 힙으로 이미 정렬이 되어있다.
다음 인덱스로 넘어가서
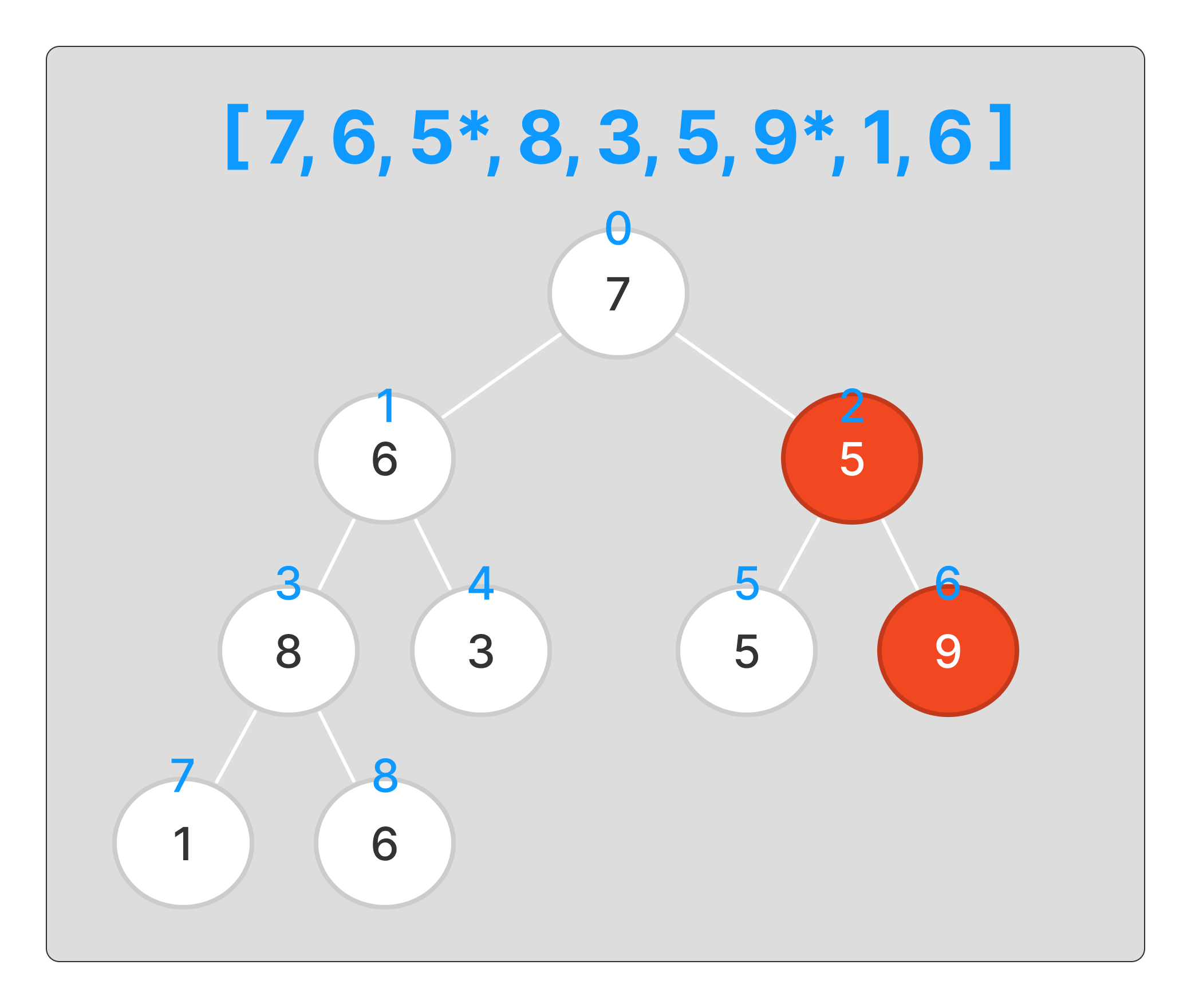
5와 9의 위치가 변경되야 한다.
이를 변경해주자.
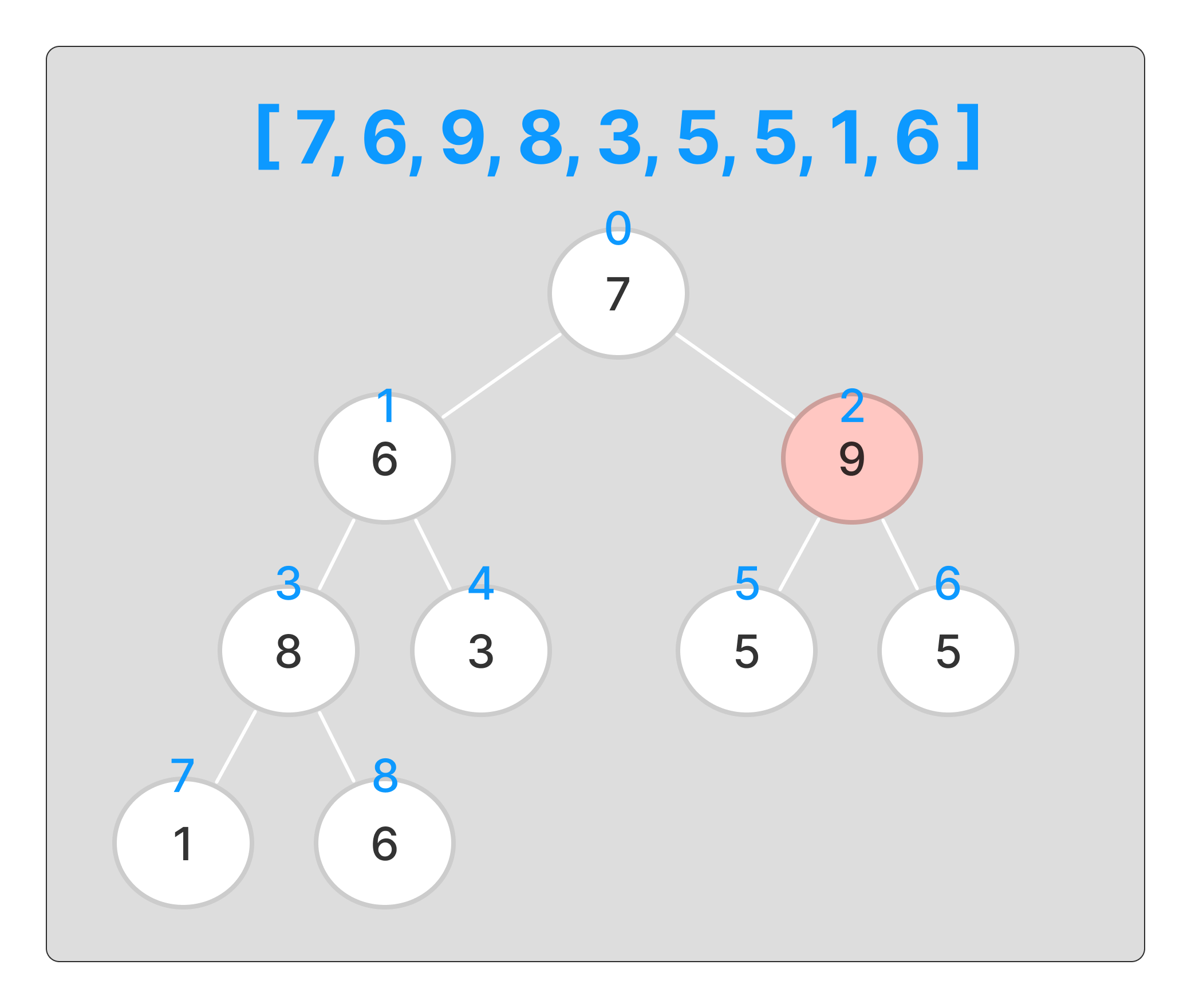
변경을 완료했으니 다음번 인덱스로 가자
여기도 최대힙을 구성하기위해 위치를 변경해야한다.
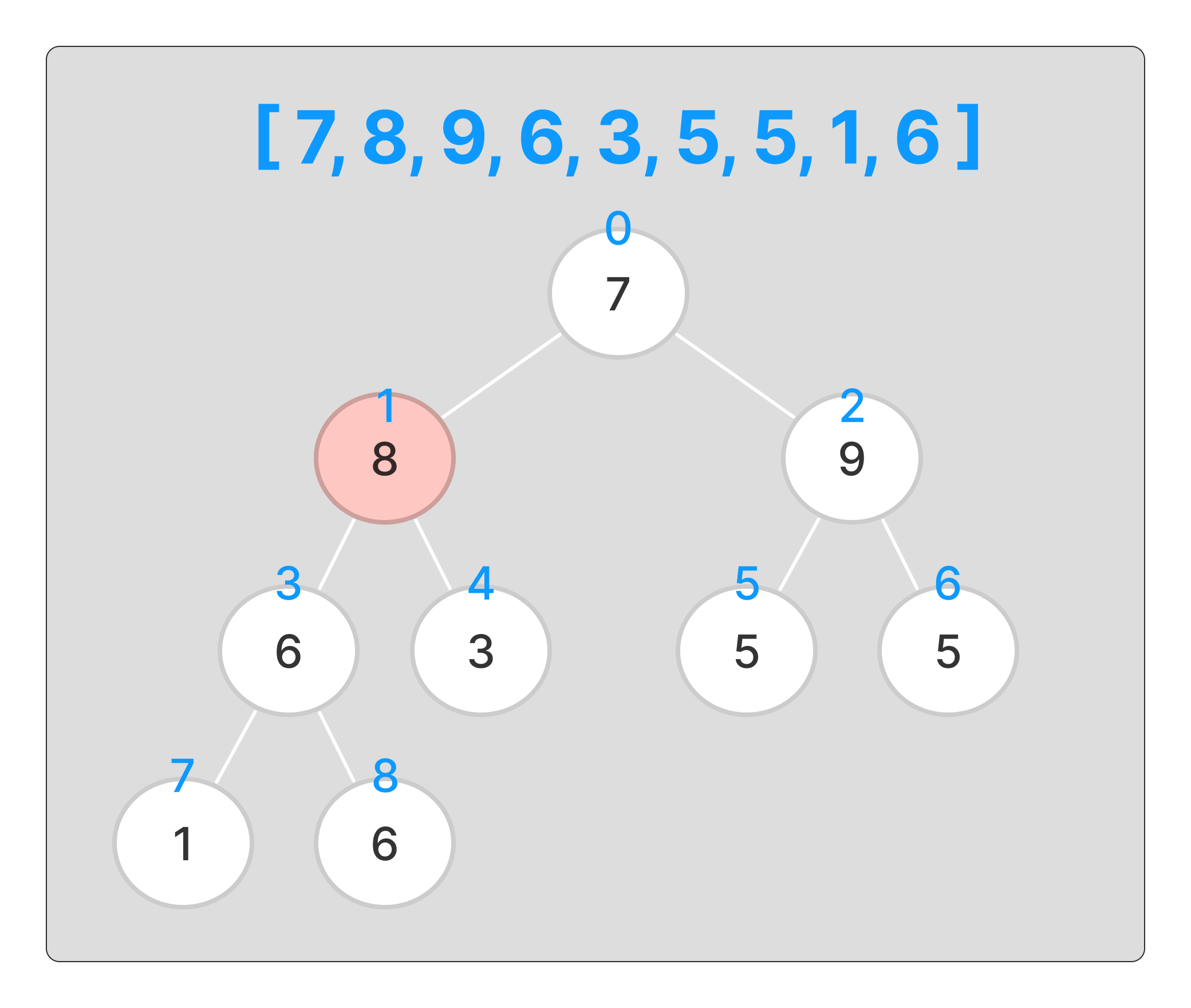
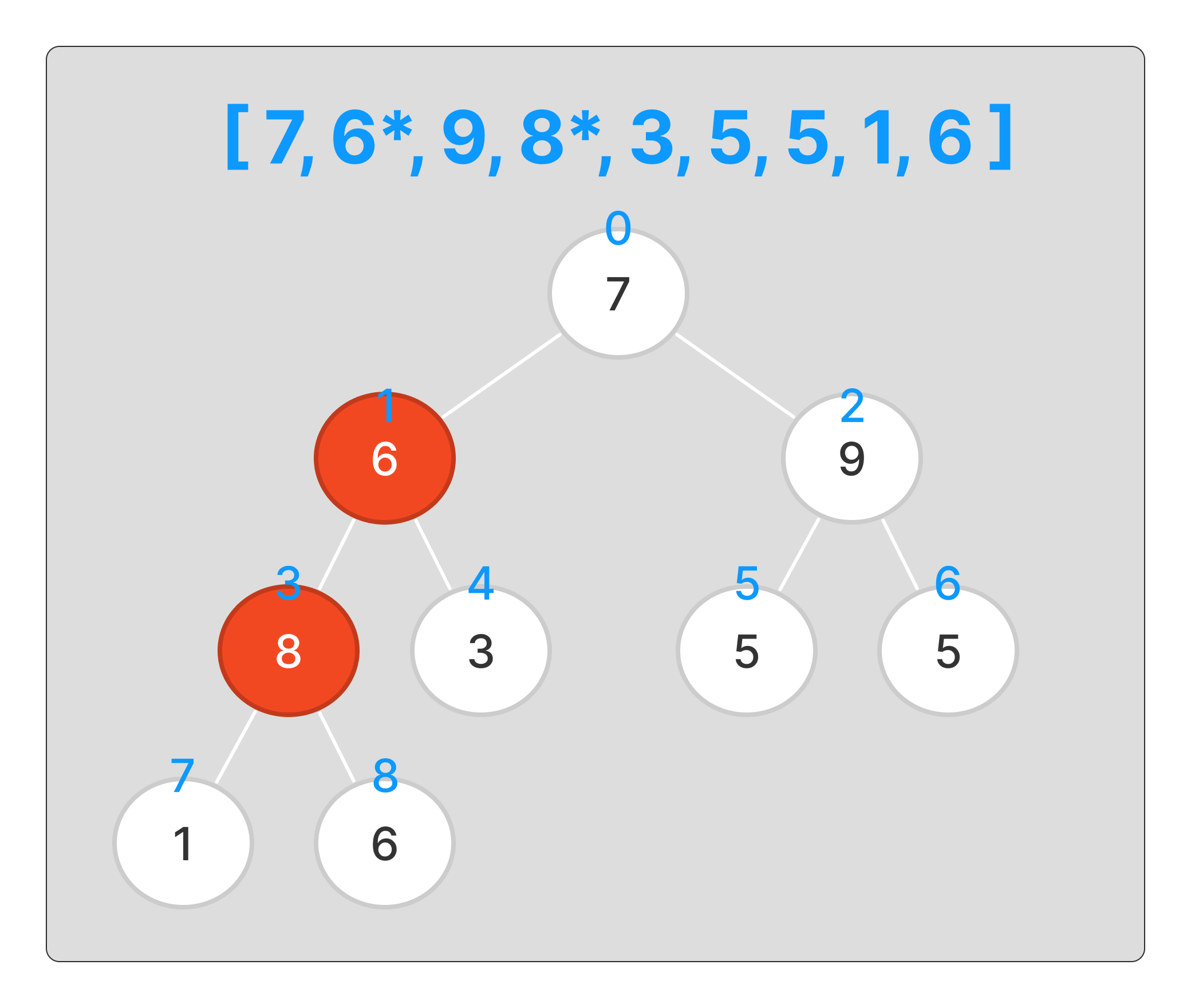
변경한 뒤에 마찬가지로 다음번 인덱스로 넘어간다.
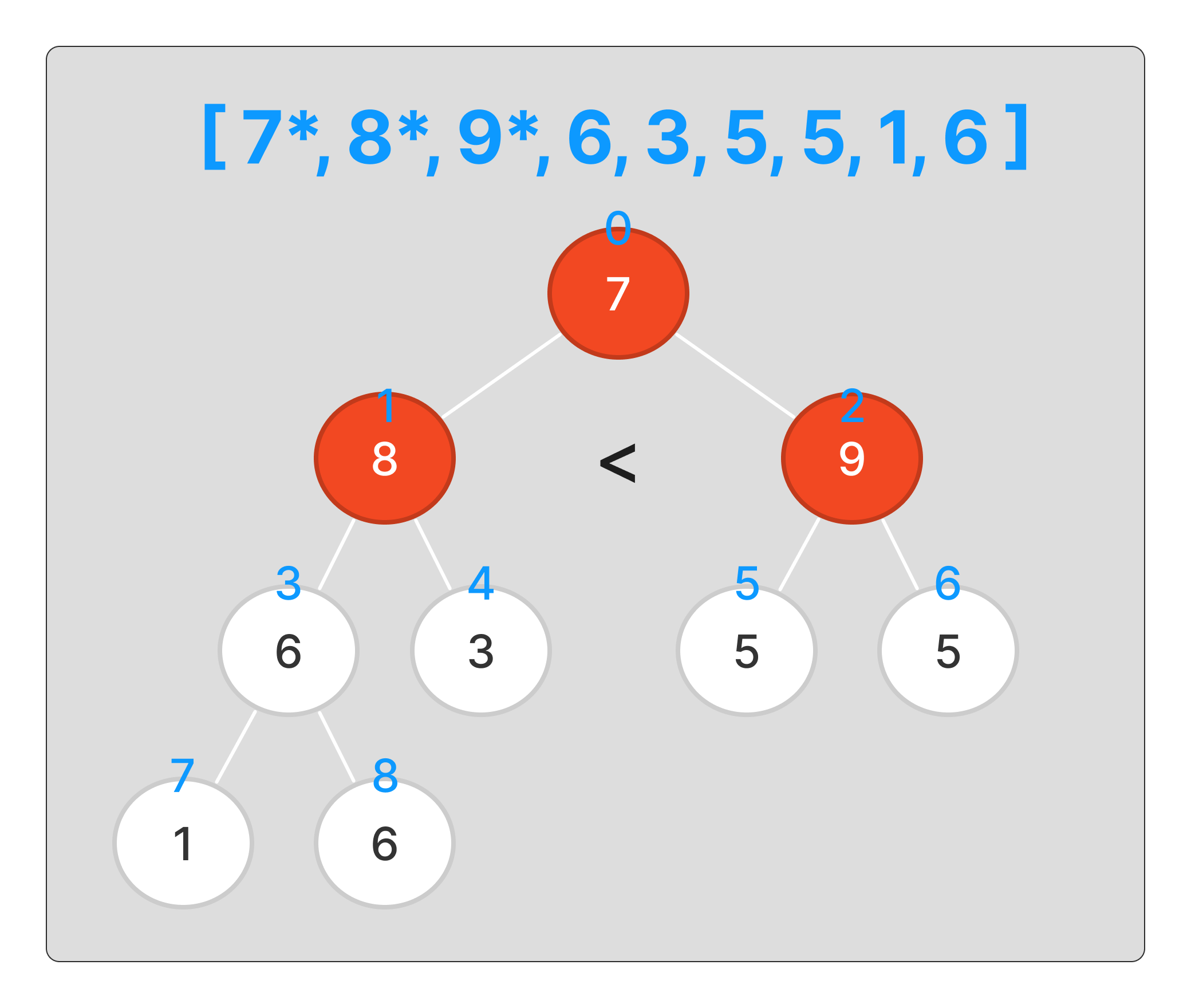
다음번 인덱스는 자식 노드 모두가 크다.
이를 비교하여 더 큰 값이 부모 노드로 오게한다.
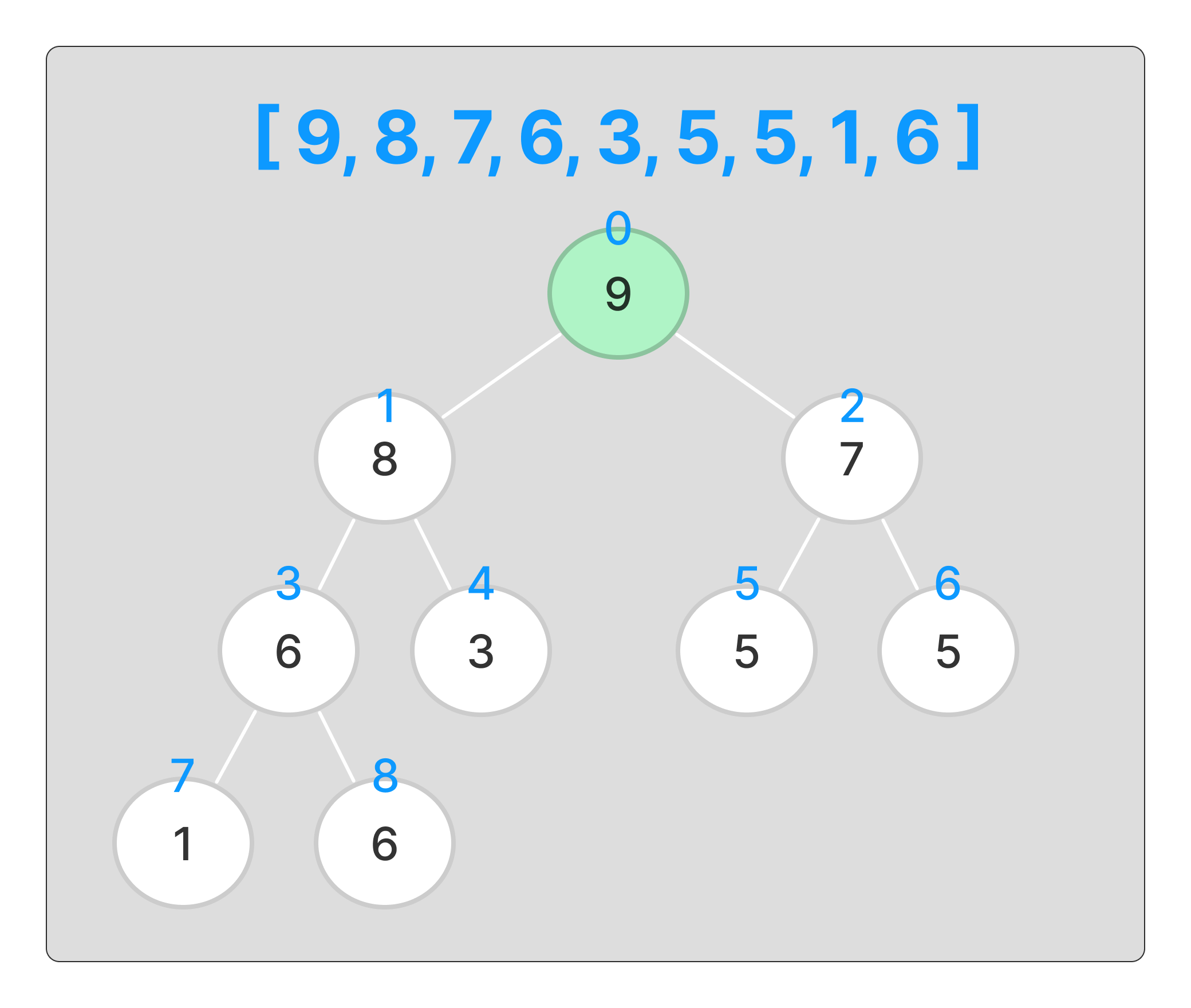
이로써 최대 힙이 생성되었다.
여기까지가 최대 힙의 생성이다.
이제 오름차순으로 정렬을 해보자.
루트 노드의 데이터가 가장 큰 수 이므로 맨 뒤의 인덱스와 자리를 변경해준다.
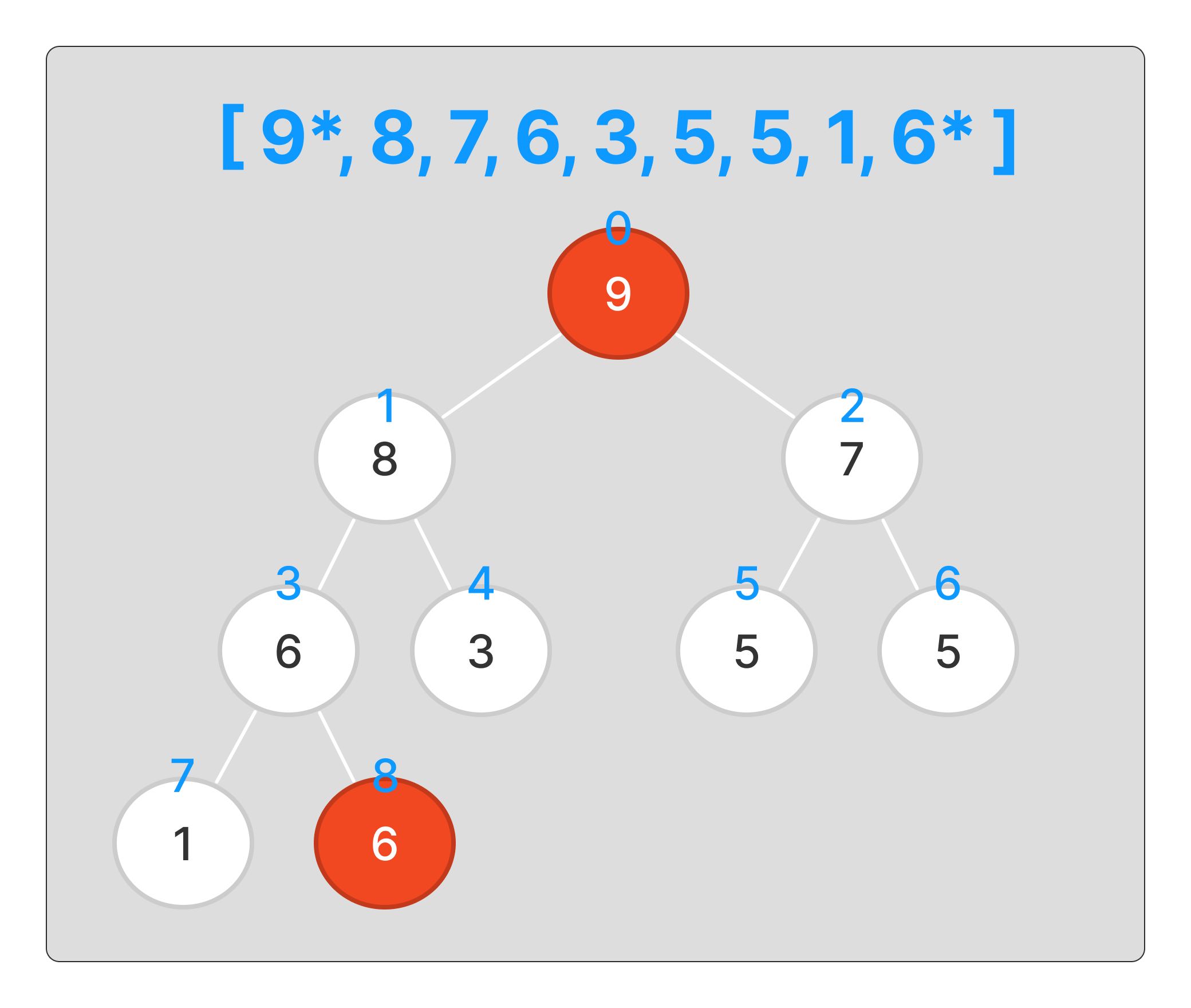
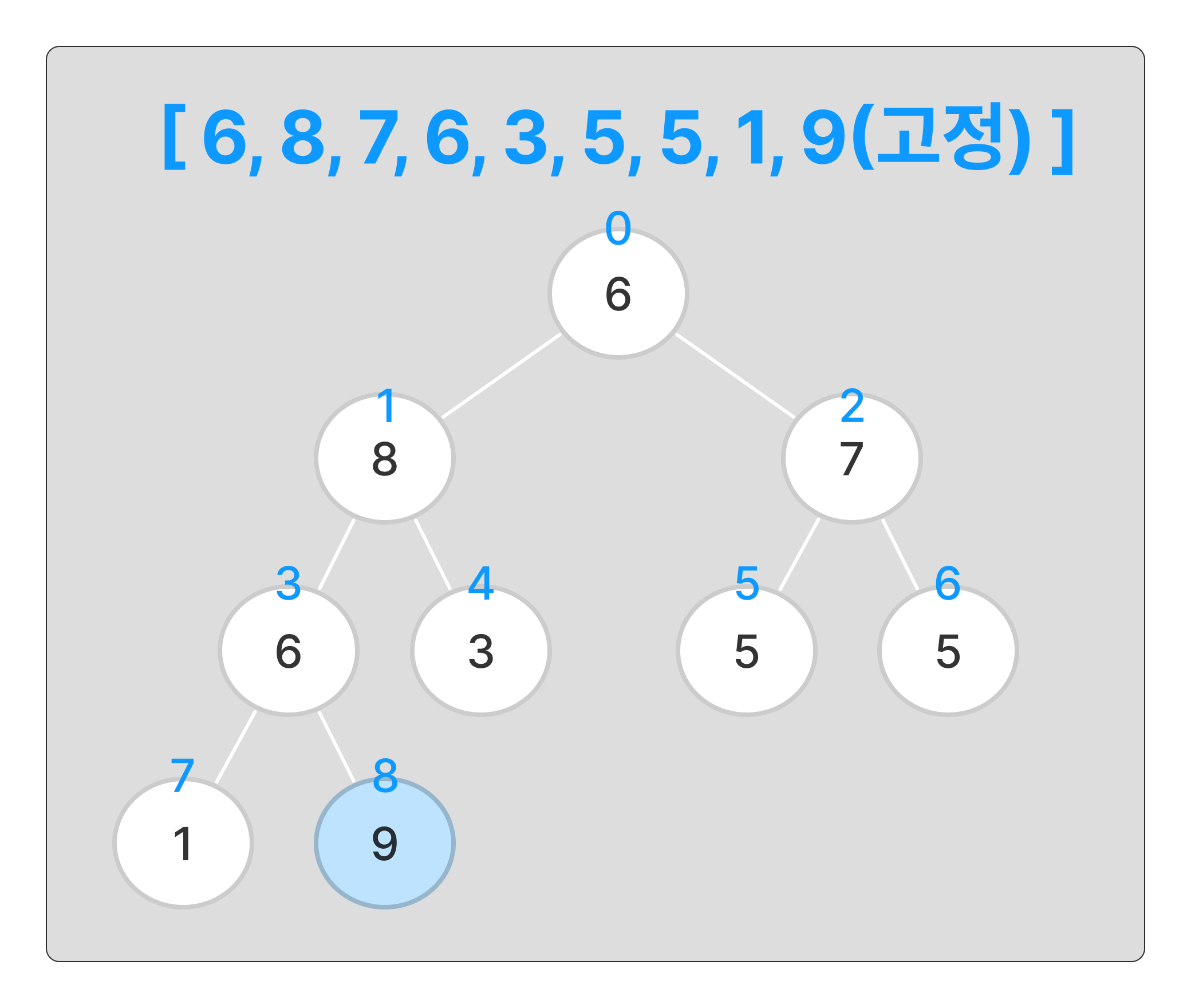
변경을 완료한 뒤에는 9가 위치한 8번 인덱스는 고정시킨다.
(코드에서는 이를 구현하기 위해 길이를 --로 축소한다.)
이제 다시 힙 생성을 과정을 반복해준다.
반복하여
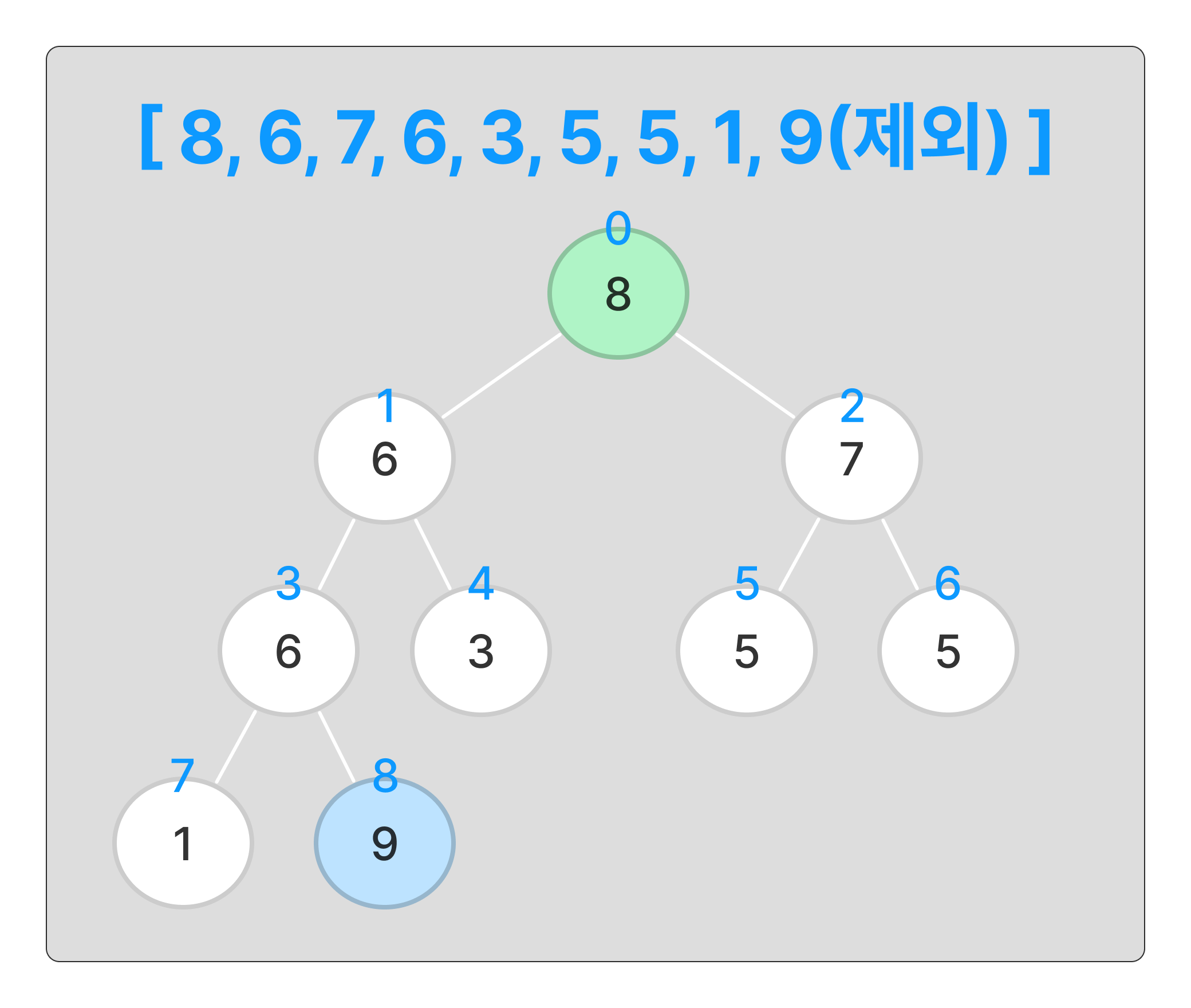
8이 루트 노드가 되며 최대 힙이 구성되었다.
고정된 9를 제외한 가장 큰 인덱스와 위치를 바꾼다.
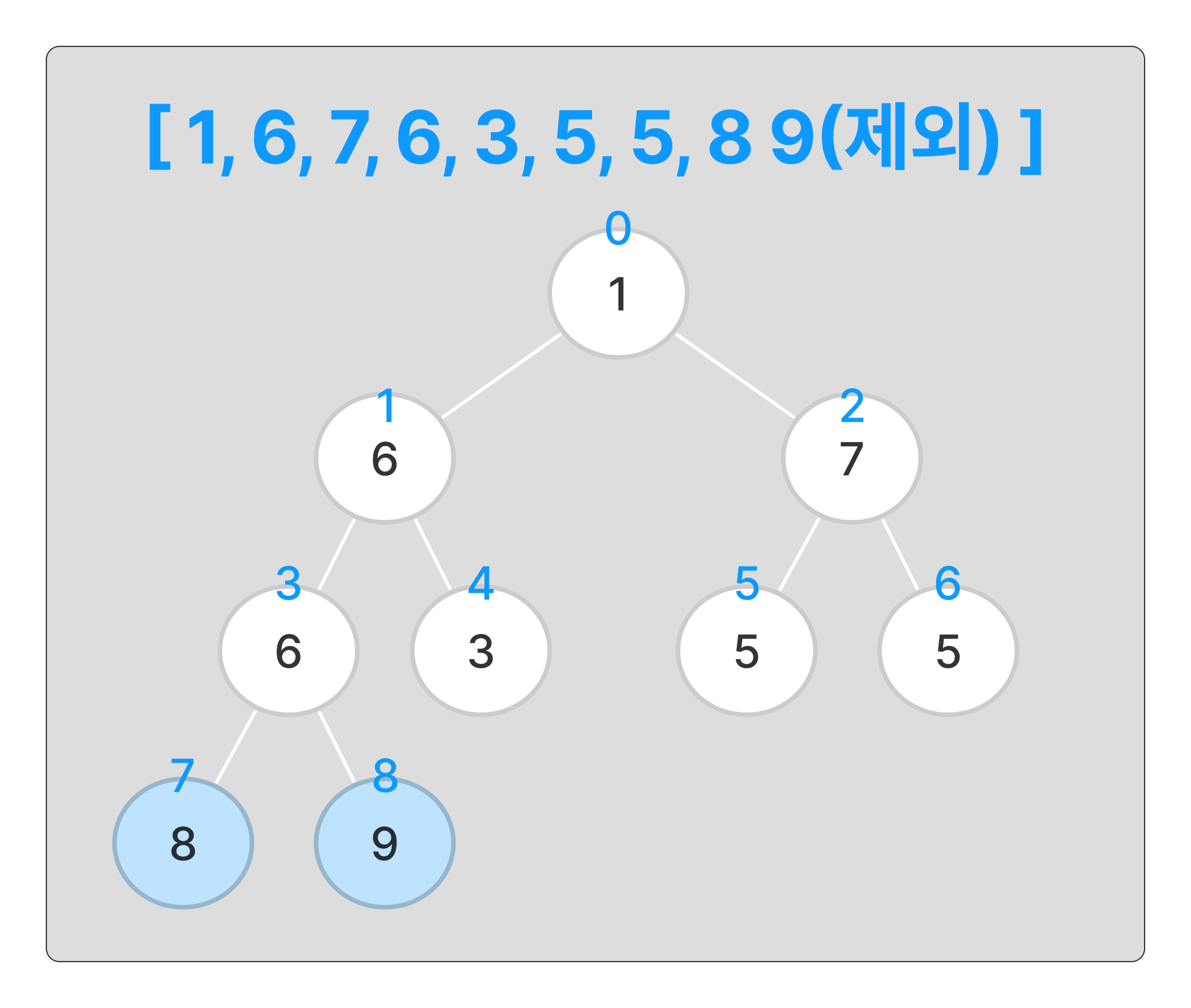
다시 힙 생성하고 스왑하는 과정을 반복한다.
최종적으로는 정렬이 완료된다.
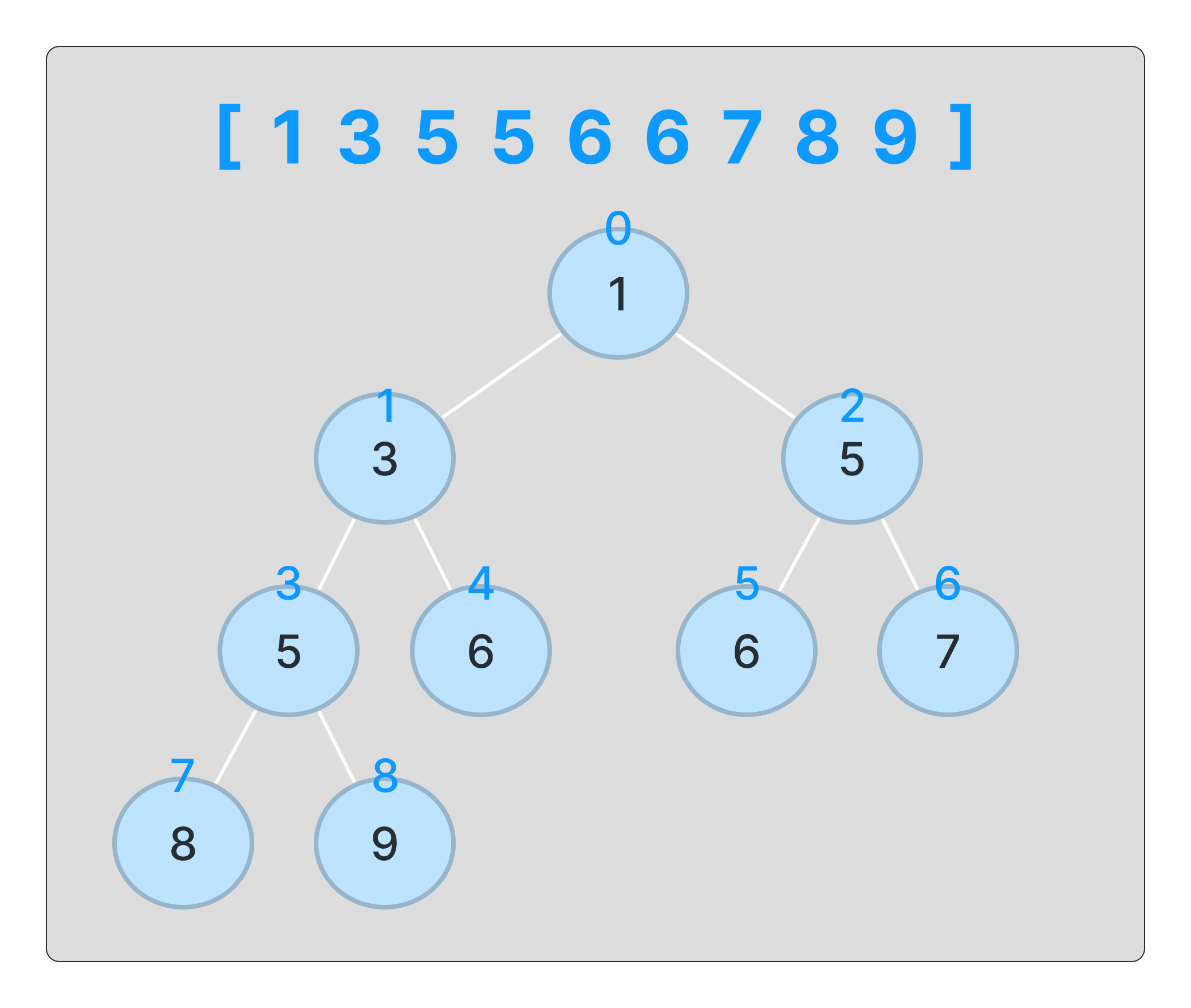
지금까지는 그림으로 표현했고,
이제는 코드로 한번 이를 표현해보자.
// 배열에서 두 요소를 교환하는 헬퍼 함수
function swap(arr, i, j) {
let temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
// 최대 힙(Max Heap)을 구성하는 함수
function buildMaxHeap(arr) {
const length = arr.length;
for (let i = Math.floor(length / 2); i >= 0; i--) {
heapify(arr, length, i);
}
}
// 힙을 조정하는 함수
function heapify(arr, length, i) {
// 왼쪽 자식 노드
const left = 2 * i + 1;
// 오른쪽 자식 노드
const right = 2 * i + 2;
// 부모 노드
let largest = i;
// 자식노드가 부모 노드보다 데이터가 클 경우 실행
if (left < length && arr[left] > arr[largest]) {
largest = left;
}
// 자식노드가 부모 노드보다 데이터가 클 경우 실행
if (right < length && arr[right] > arr[largest]) {
largest = right;
}
// 부모 노드와 자식 노드의 데이터 스왑
// 힙 생성 실행
if (largest !== i) {
swap(arr, i, largest);
heapify(arr, length, largest);
}
}
// 힙 정렬 함수
function heapSort(arr) {
let length = arr.length;
// 최대 힙을 구성
buildMaxHeap(arr);
for (let i = length - 1; i > 0; i--) {
// 최대값을 배열 끝으로 보내기
swap(arr, 0, i);
// 힙 크기 축소 (정렬된 것 제외)
length--;
// 힙을 재조정 (힙 생성)
heapify(arr, length, 0);
}
}
const data = [7, 6, 5, 8, 3, 5, 9, 1, 6];
heapSort(data);처음 heapSort()를 실행하고,
buildMaxHeap()을 이용해 최대힙을 생성한다.
buildMaxHeap()에서는 배열의 길이를 절반으로 하여 반복문을 시작한다.
인덱스를 하나씩 줄여가며 노드를 비교한다.
부모 노드와 자식 노드는 일정한 규칙을 가지고 있는데, 위에서 지수적으로 2씩 커지는 구조이기 때문에 부모 노드와 자식노드는 n과 2n + 1, 2n + 2 관계를 이룬다.
ex) 만약 3개씩 나누어 졌다면, n과 3n + 1, 3n + 2, 3n + 3이 되었을 것.
아무튼 위의 구조에 따라서 left와 right의 값을 결정한다.
그 후에 자식 노드가 부모 노드보다 인덱스가 작은지 판별후 자식 노드의 데이터가 부모 노드보다 크면, 자식 노드의 인덱스를 부모 노드의 인덱스로 저장한 뒤 오른쪽 노드도 바뀐 부모 노드와 비교를 함으로 자식 노드간의 대소를 비교한다.
부모노드의 인덱스가 처음과 달라졌다면, 데이터의 swap()을 진행한다.
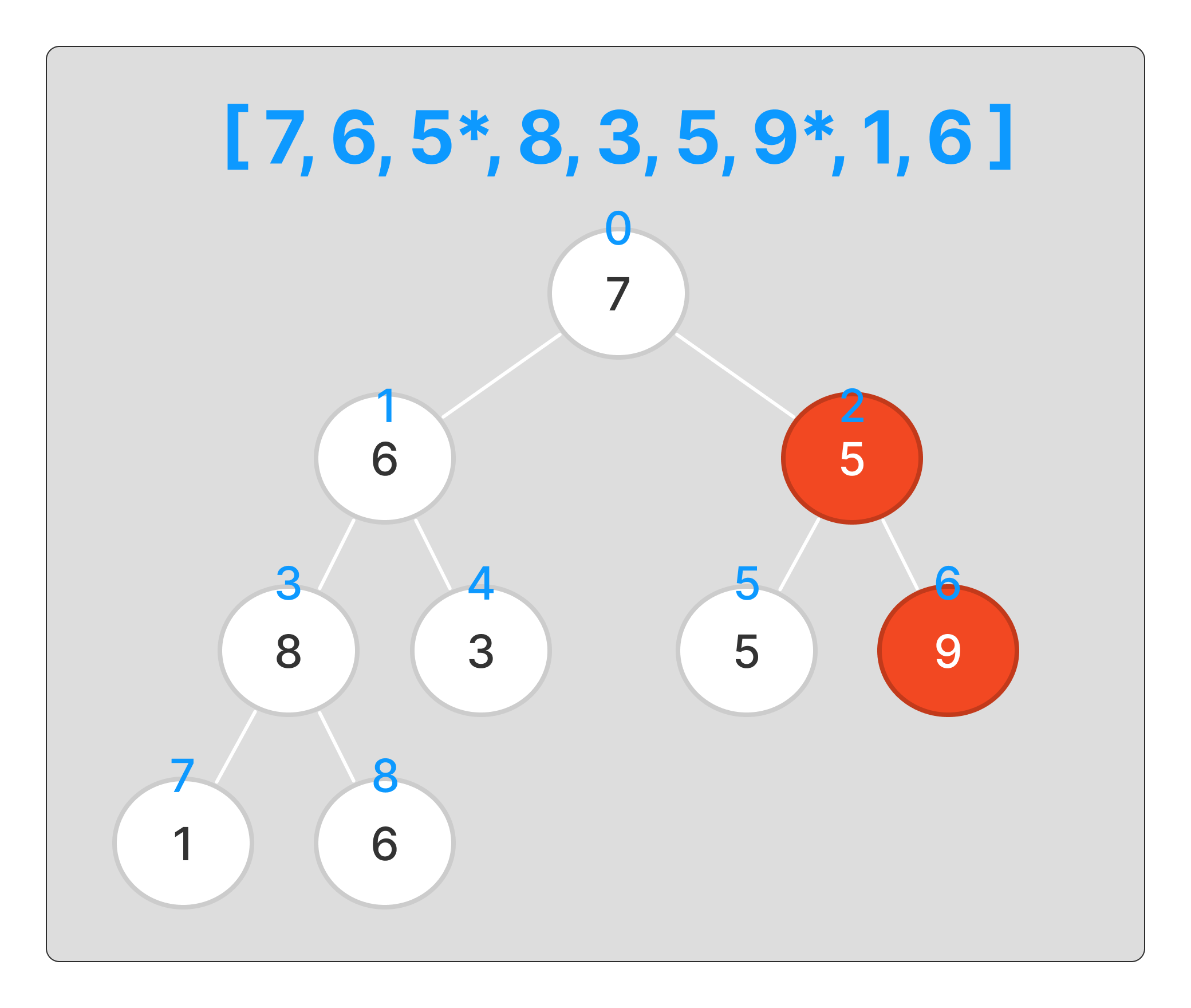
이 부분에 해당한다.
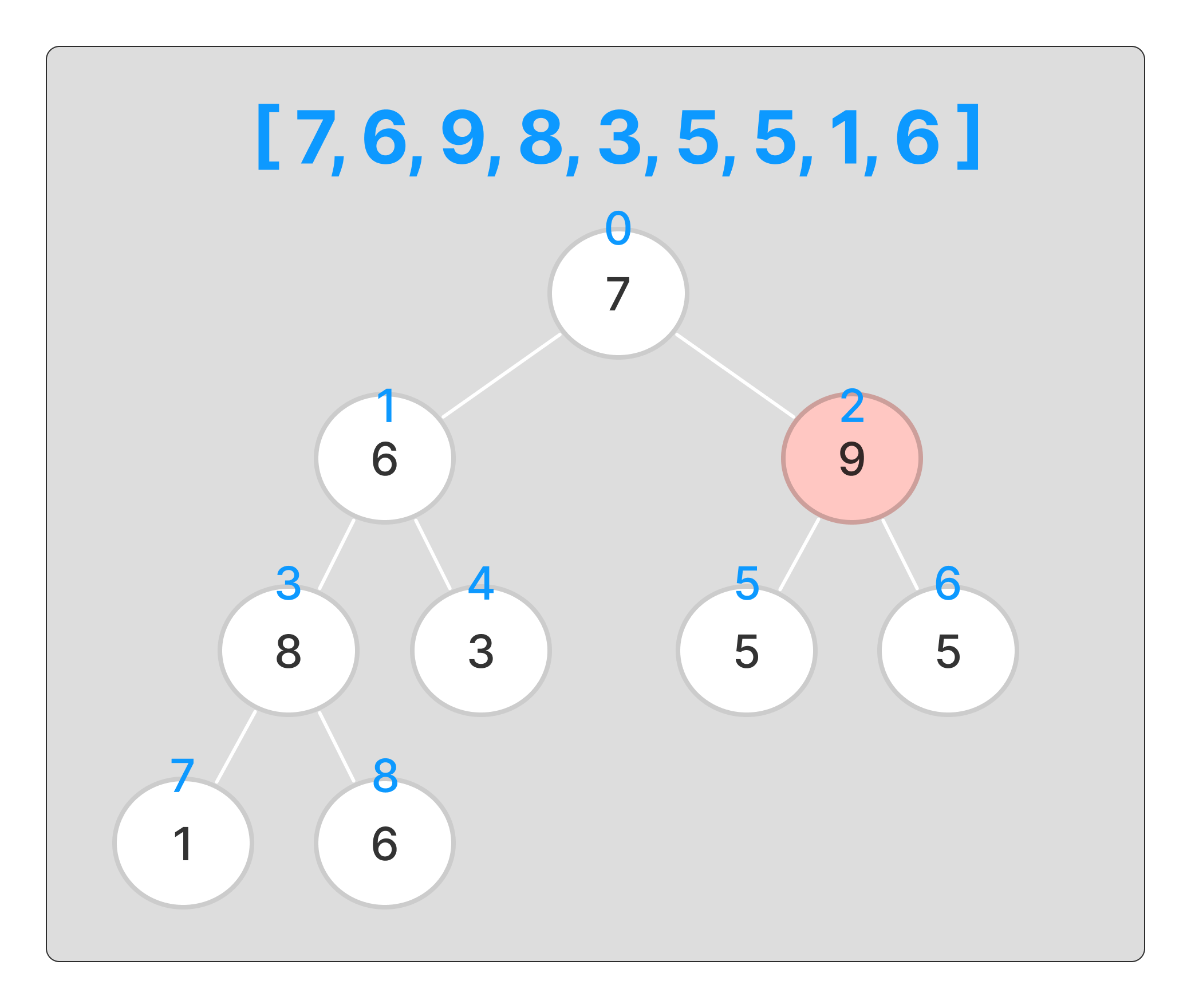
데이터를 바꾸고 바뀐 노드에 대해서 힙 생성 알고리즘을 사용한다.
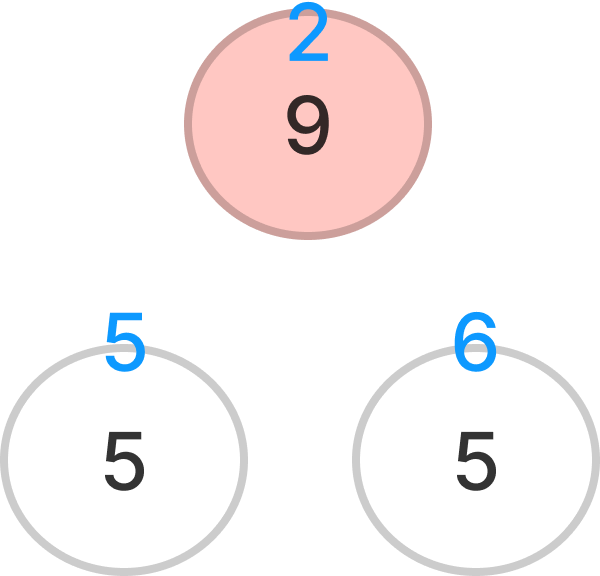
데이터가 잘 변환되었으니 마치고 buildMaxHeap()의 for문으로 돌아가 다음 인덱스에 대해서 실행한다.
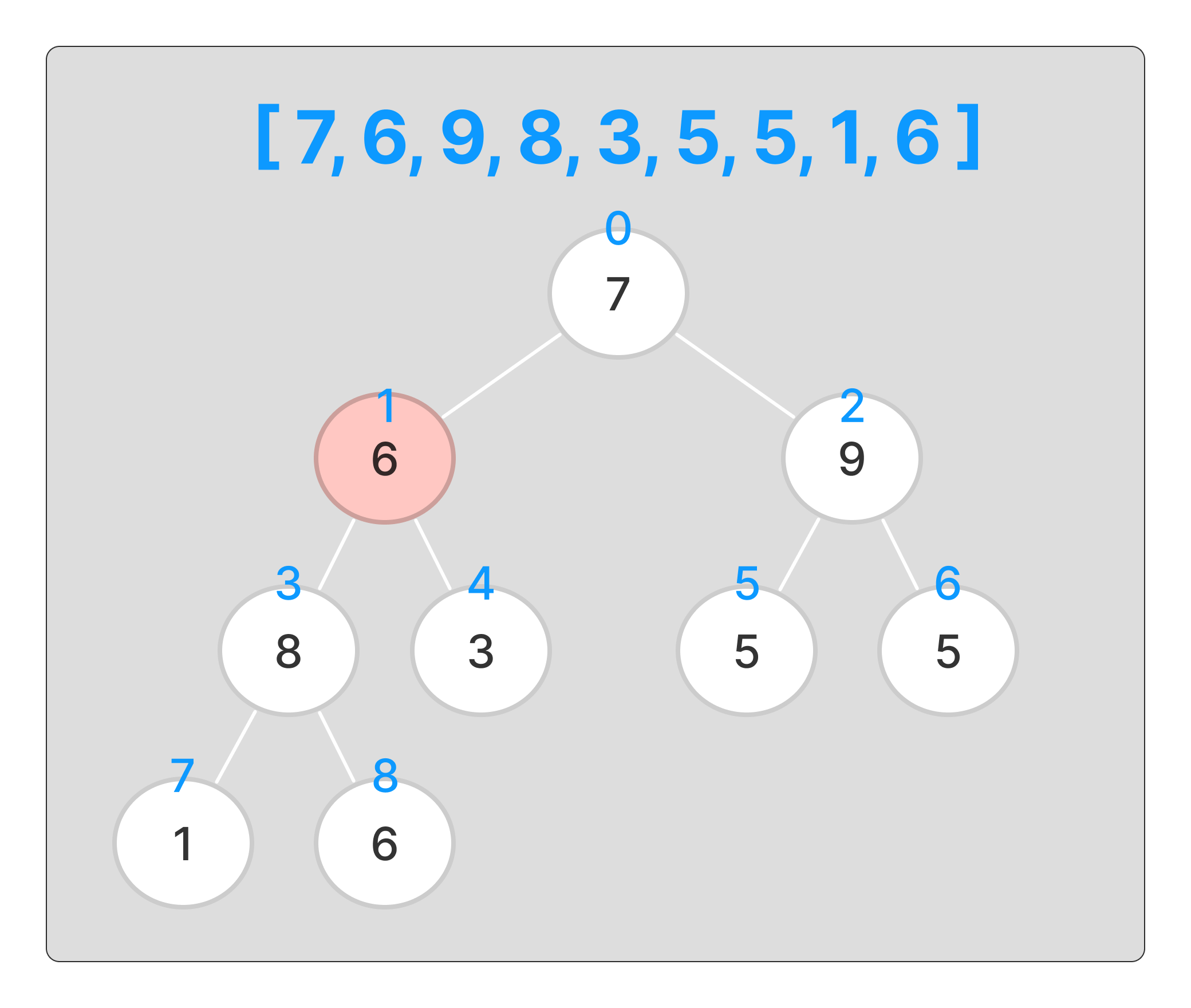
마찬가지로 정렬을 해주고 최종적으로
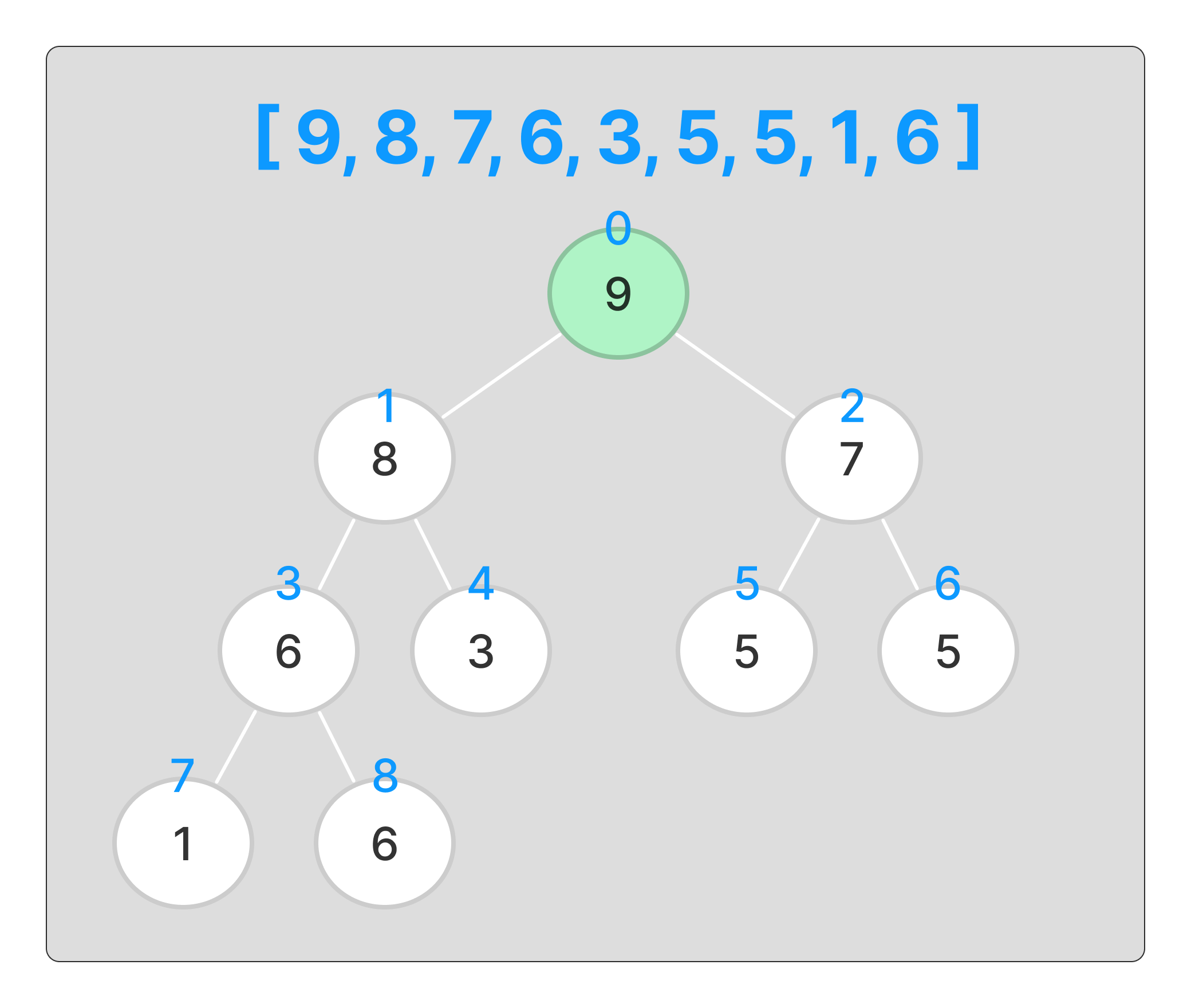
최대힙을 만들어준다.
buildMaxHeap()을 마치고 값을 끝으로 보낸다.
이 과정을 반복하여 정렬한다.
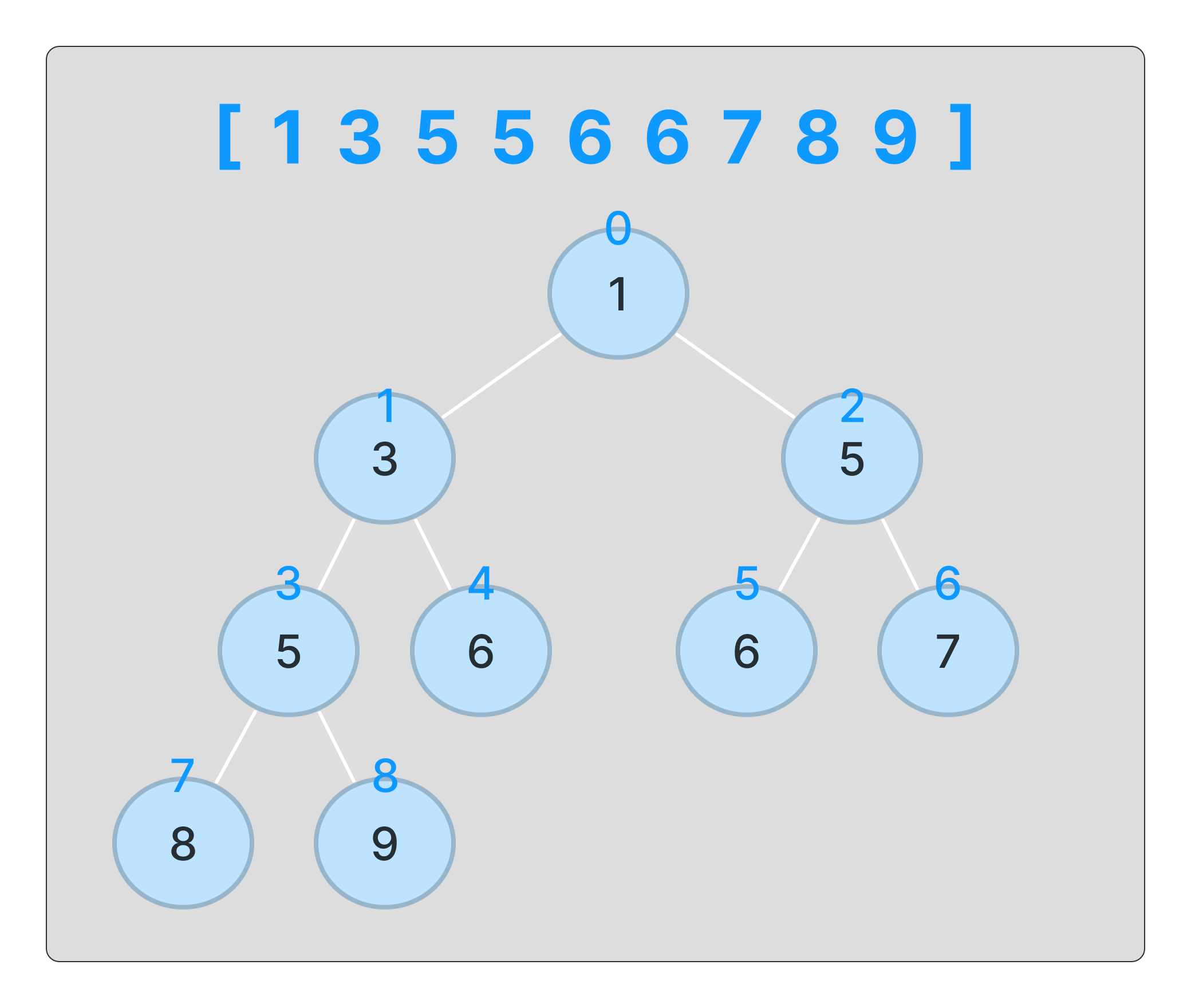
1 3 5 5 6 6 7 8 9 가 최종적으로 완성이 되고 함수가 종료된다.
이로써 힙 정렬은 끝났다.
선수 지식으로 알아야할 자료구조의 내용과 힙 정렬의 과정이 복잡하여, 내용이 길어졌다.
하지만, 힙이라는 개념은 자바스크립트의 데이터를 저장하는 구조이기도 하고 대표적인 자료구조의 한 형태이므로 반드시 알아두어야한다.
