Merge Sort(병합 정렬)

퀵 정렬과 마찬가지로 분할 정복을 채택한 알고리즘이다

퀵 정렬은 피벗값(기준값)에 따라서 결과가 편향되지만,

병합정렬은 절반씩 나눠서 진행하므로 시간복잡도 n log(n)이 보장된다.

1. Merge Sort(병합 정렬) 문제

예제를 통해서 병합 정렬을 한 번 알아보자

다음의 숫자들을 오름차순으로 정렬하는 프로그램을 작성하라.

7 6 5 8 3 5 9 1

2. Merge Sort(병합 정렬) 풀이

7 6 5 8 3 5 9 1를 반씩 나눠서

7,6,5,8,3,5,9,1 로 시작한다

두 가지씩 병합하여

6 7, 5 8, 3 5, 1 9 를 만든다

5 6 7 8, 1 3 5 9를 만든다

최종적으로 1 2 3 4 5 6 7 8을 만들고 종료한다

병합 정렬이 n logn 인 이유는

너비가 n, 깊이가 지수적으로 커지므로 2^n log2(n)으로 증가한다

따라서 너비 * 깊이 = n log(n)을 따르게 된다

// 다음의 배열을 오름차순으로 정렬하시오
const mergeArr = [6, 7, 1, 3, 5, 8, 2, 4];

// 메모리 사용문제로 전역에 선언
// sorted 배열의 크기가
let sorted = [...mergeArr];

function merge(data, start, mid, end) {
	let i = start;
	let j = mid + 1;
	let k = start;

	while (i <= mid && j <= end) {
		if (data[i] <= data[j]) {
			sorted[k] = data[i];
			i++;
		} else {
			sorted[k] = data[j];
			j++;
		}
		k++;

		console.log(sorted);
	}

	if (i > mid) {
		for (let l = j; l <= end; l++) {
			sorted[k] = data[l];
			k++;
		}
	} else {
		for (let l = i; l <= mid; l++) {
			sorted[k] = data[l];
			k++;
		}
	}

	for (let l = 0; l < data.length; l++) {
		mergeArr[l] = sorted[l];
	}
}

function mergeSort(data, start, end) {
	// 배열의 크기가 2 이상일 경우에만 실행한다
	if (start < end) {
		// 중간값을 구해 소숫점을 버린다
		let middle = Math.floor((start + end) / 2);

		// data에는 길이 8의 [6, 7, 1, 3, 5, 8, 2, 4]가 들어가고
		// 재귀함수에서도 같이 들어가나
		// 사용하는 범위가 점점 줄어든다, start와 end가 같아 질때까지 ==> start === end === 1
		mergeSort(data, start, middle);
		mergeSort(data, middle + 1, end);

		// 배열을 병합하는 부분이다
		merge(data, start, middle, end);
	}
}

mergeSort(mergeArr, 0, mergeArr.length - 1);
console.log(mergeArr);

위의 과정을 console.log와 그림을 통해서 살펴보자.

아래의 배열은 sorted를 merge함수의 for문 안에서 찍었을 때의 콘솔이다.

sorted 배열을 이용해 왼쪽부터 짝지어 배열을 맞춘후 합쳐지는 과정을 볼 수 있다.

[6, 7, 1, 3, 5, 8, 2, 4]
[6, 7, 1, 3, 5, 8, 2, 4]
[1, 7, 1, 3, 5, 8, 2, 4]
[1, 3, 1, 3, 5, 8, 2, 4]
[1, 3, 6, 7, 5, 8, 2, 4]
[1, 3, 6, 7, 5, 8, 2, 4]
[1, 3, 6, 7, 2, 8, 2, 4]
[1, 3, 6, 7, 2, 4, 2, 4]
[1, 3, 6, 7, 2, 4, 5, 8]
[1, 2, 6, 7, 2, 4, 5, 8]
[1, 2, 3, 7, 2, 4, 5, 8]
[1, 2, 3, 4, 2, 4, 5, 8]
[1, 2, 3, 4, 5, 4, 5, 8]
[1, 2, 3, 4, 5, 6, 5, 8]
[1, 2, 3, 4, 5, 6, 7, 8]
[1, 2, 3, 4, 5, 6, 7, 8]

하지만 이렇게 보면 헷갈릴 수 있으니 그림을 통해서 한번 더 살펴보자

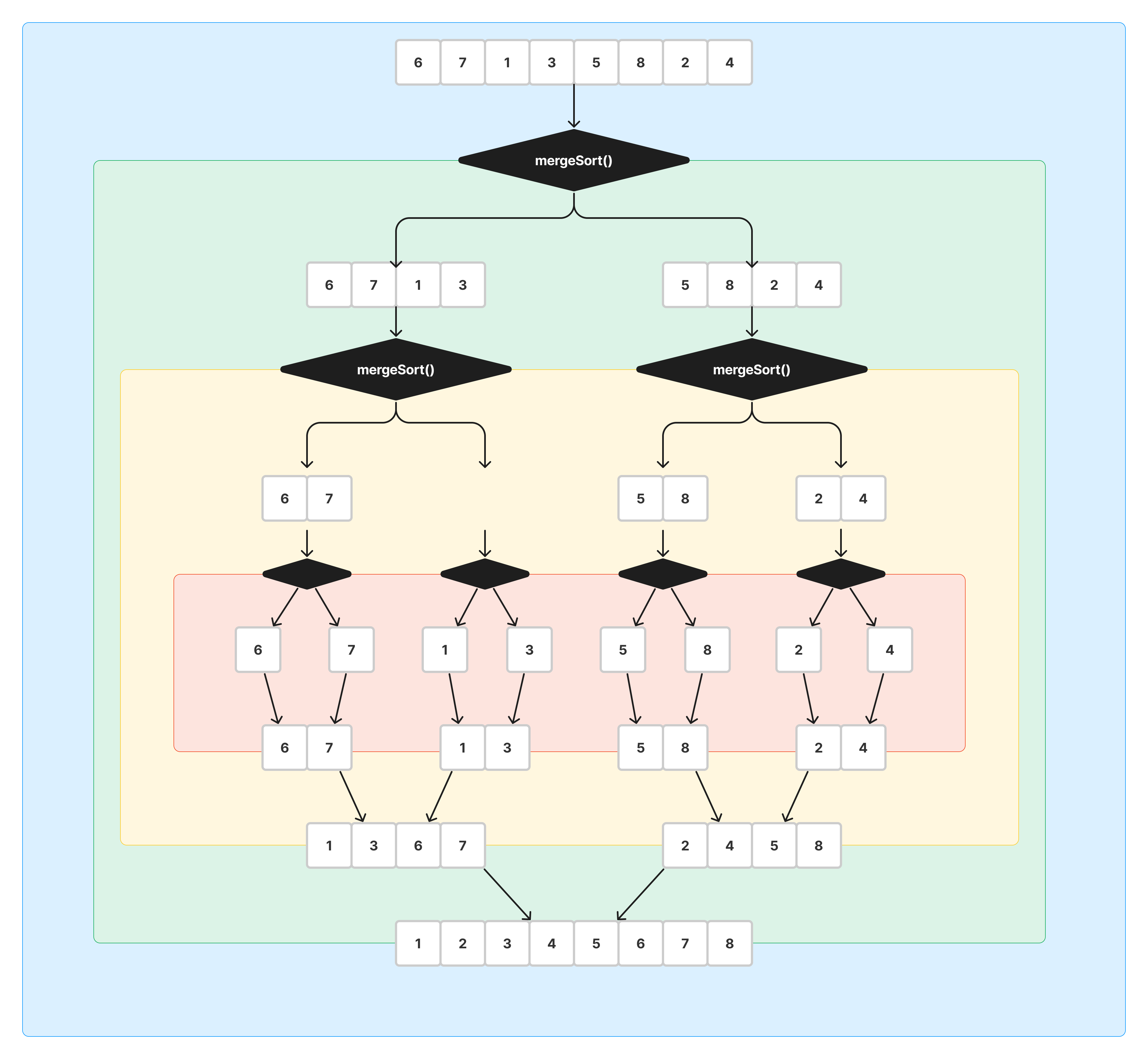
그림을 보면 길이 8의 배열이 첫번째 mergeSort를 만나 안에서 재귀함수 mergeSort를 만나는 것을 볼 수 있다

이를 반복실행하여 붉은영역까지 도달한 후 위에서 본 콘솔처럼 순서를 맞춰가는 과정이다.

각 색상별 영역은 함수가 실행중임을 나타낸다

3. Merge Sort(병합 정렬)의 효율성

효율성을 알기위해 설명해보자면

6 7, 5 8를 한번 살펴보자

위의 두 숫자는 정렬이 된 집합이므로

숫자가 작은 왼쪽부터 각각 i, j의 인덱스를 주어 비교한다

arr1[i] = 6과 arr2[j] = 5 를 비교하고

5가 더 작으므로 새로운 배열에 넣은 뒤에

j를 1증가시킨다

arr1[i] = 6과 arr2[j+1] = 8을 비교하여

6을 배열에 넣고 i를 증가시킨다

이런식으로 이미 정렬이 된 배열을 가지고 정렬을 수행하기 때문에

너비는 시간복잡도 O(n)을 갖게된다

아래로 깊어지는 깊이는 처음에 n번 비교하고

그 다음엔 n/2번, 그 다음엔 n/2^2번,

차례대로 n/2^m 만큼 지수적으로 증가하기 때문에

밑이 2인 로그 log(n), 시간복잡도 O(log(n))을 갖는다

따라서 병합정렬은 시간복잡도 O(n log(n))을 따른다

참고자료

동빈나 유튜브
https://www.youtube.com/watch?v=qQ5iLNjpxSk&list=PLRx0vPvlEmdDHxCvAQS1_6XV4deOwfVrz