성능 요약
메모리: 13236 KB, 시간: 128 ms
분류
다이나믹 프로그래밍
제출 일자
2024년 1월 18일 17:20:40
문제 설명
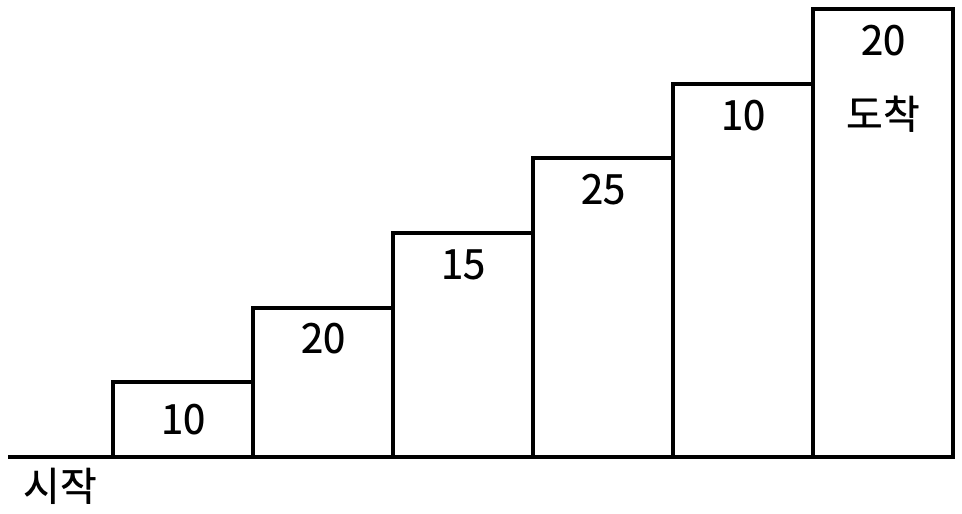
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점수를 얻게 된다.
예를 들어 <그림 2>와 같이 시작점에서부터 첫 번째, 두 번째, 네 번째, 여섯 번째 계단을 밟아 도착점에 도달하면 총 점수는 10 + 20 + 25 + 20 = 75점이 된다.
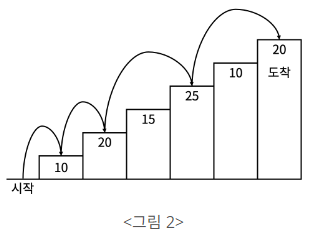
계단 오르는 데는 다음과 같은 규칙이 있다.
계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다.
연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다.
마지막 도착 계단은 반드시 밟아야 한다.
따라서 첫 번째 계단을 밟고 이어 두 번째 계단이나, 세 번째 계단으로 오를 수 있다. 하지만, 첫 번째 계단을 밟고 이어 네 번째 계단으로 올라가거나, 첫 번째, 두 번째, 세 번째 계단을 연속해서 모두 밟을 수는 없다.
각 계단에 쓰여 있는 점수가 주어질 때 이 게임에서 얻을 수 있는 총 점수의 최댓값을 구하는 프로그램을 작성하시오.
입력
입력의 첫째 줄에 계단의 개수가 주어진다.
둘째 줄부터 한 줄에 하나씩 제일 아래에 놓인 계단부터 순서대로 각 계단에 쓰여 있는 점수가 주어진다. 계단의 개수는 300이하의 자연수이고, 계단에 쓰여 있는 점수는 10,000이하의 자연수이다.
출력
첫째 줄에 계단 오르기 게임에서 얻을 수 있는 총 점수의 최댓값을 출력한다.
코드
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt(); // 계단의 수
int[] stairs = new int[N+1];
for (int n=1; n<=N; n++) { // 계단당 점수 입력
stairs[n] = sc.nextInt();
}
if (N==1) {
System.out.println(stairs[1]);
return;
} else if (N==2) {
System.out.println(stairs[1]+stairs[2]);
return;
} else if (N==3) {
System.out.println(Math.max(stairs[1]+stairs[3], stairs[2]+stairs[3]));
return;
}
int[] dp = new int[N+1]; // 각 계단에 올랐을 때 얻을 수 있는 최대 점수
dp[1] = stairs[1];
dp[2] = dp[1]+stairs[2];
// dp3 은 1번째+3번째, 2번째+3번째 중 큰 것
dp[3] = Math.max( dp[1]+stairs[3] , stairs[2]+stairs[3] );
for (int n=4; n<=N; n++) {
// dp[n] = (2번째 전dp + 마지막 칸), (3번째 전dp + 1번째 전 + 마지막 칸) 중 큰 것
dp[n] = Math.max(dp[n-2]+stairs[n], dp[n-3]+stairs[n-1] + stairs[n]);
}
System.out.println(dp[N]);
}
}
풀이
3학년 때 알고리즘 수업시간에 배운 문제같은데 볼 때마다 또 새롭다.
i) 2번째 전 칸을 밟고 N번째 칸을 밟는 경우와
ii) 1번째 전 칸을 밟고 N번째 칸을 밟는 경우 중 큰 것
을 dp[N] 이라 뒀는데
'2번째 전 칸을 밟는 경우' 는 그 전에 뭘 밟았든 상관없으므로 dp[N-2],
'1번째 전 칸을 밟는 경우' 는 두 번째 전을 밟으면 안 되므로 (3연속 밟게 되니)
'3번째 전을 밟고 1번째 전을 밟고 N을 밟는 경우' 로 생각하여서 점화식(?)을 다음과 같이 짰다.