TIL11: Data Structure - 4 [ Tree / Binary Search Tree]

Tree(트리)

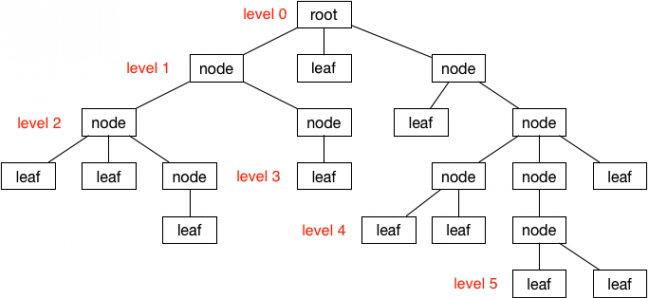
• 특징
  • Node(노드)로 구성된 계층적 자료 구조
  • Root Node: 최상위에 위치한 값이 null인 노드
  • Parent(부모 노드), Child(자식 노드): 루트 노드를 만들고, 거기에 child를 추가, 또 그 child에 child를 추가하는 방식으로 구조 구현
  • Depth(깊이): 루트 노드를 기준으로 노드로 접근하기 위한 거리
  • Height(높이): '깊이'에 반대 방향으로 접근하는 거리
  • Leaf: 자식 노드가 없는 노드

Binary Search Tree(이진 탐색 트리)

• 특징
  • 최대 2개의 자식만 갖는 트리 구조
  • 구조가 재귀적이므로, 자식 노드 또한 최대 2개의 자식 노드를 가짐
• 노드의 순서
  • 왼쪽 Sub Tree에는 노드의 값보다 작은 값
  • 오른쪽 Sub Tree에는 노드의 값과 같거나 보다 큰 값
• 순회 방법
  • DFS(Depth First Search, 깊이 우선 탐색): 좀더 집중
  • BFS(Breadth First Search, 너비 우선 탐색)
• 종류
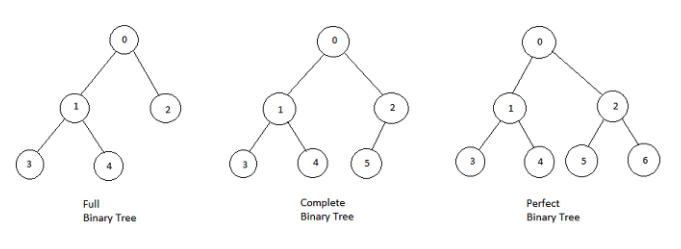
  • Full Binary Tree(정 이진 트리): 모든 노드들의 child 갯수가 0 아니면 2인 이진 트리
  • Complete Binary Tree(완전 이진 트리): 왼쪽 서브 트리부터 오른쪽 서브트리로 채워져서 현재까지 빠짐 없이 노드가 채워진 이진 트리
  • Perfect Binary Tree(포화 이진 트리): 모든 노드들의 child 갯수가 2인 이진 트리
• 탐색 순서에 따른 순회
  • Preorder Traversal(전위 순회): 부모 -> 좌 -> 우
  • Inorder Traversal(중위 순회): 좌 -> 부모 -> 우
  • Postorder Traversal(후위 순회): 좌 -> 우 -> 부모

• BST Big O 표기(Average Cases)

  • 가져오기: O(log(n))
  • 추가하기: O(log(n))
  • 삭제하기: O(log(n))

• BST Big O 표기(Worst Cases)

  • 가져오기: O(n)
  • 추가하기: O(n)
  • 삭제하기: O(n)

자료 출처: 코드스테이츠(CodeStates)