자료구조 1강 복습

사진: Unsplash의Christian Joudrey

목차
1-1 데이터 구조
1-2 알고리즘
1-3 알고리즘의 성능 평가 방법

---

1-1 데이터 구조

데이터 정의

• 기능적 정의: 의미있는 모든 값
• 의미론적 정의: 사람이나 자동 동작기기가 생성하고 처리하는 형태의 정보

데이터 구조 정의

• 프로그램에 저장된 데이터를 효율적으로 저장 ⋅ 조직하는 방법

데이터 구조 필요성

• 프로그램에 저장된 데이터에 대해 효율적으로 탐색 ⋅ 삽입 ⋅ 수정의 연산을 수행하기 위하여

추상데이터타입 정의

• 데이터 & 연산(기능)
• 예시: 스택의 추상데이터타입(ADT)는 스택 구조에 넣을 수 있는 데이터와 스택의 연산(기능)을 정의한 것

자료구조 - 추상데이터타입 관계

• 추상데이터타입(ADT)을 구현하여 구체화한 것이 자료구조

자료구조 종류

• 스택: 쌓아 놓는 것
• 큐: 놀이공원 줄
• 리스트: 체크 리스트
• 딕셔너리: 영한사전
• 그래프: 지도
• 트리: 조직도

---

1-2 알고리즘

알고리즘 정의

• 문제해결을 위한 단계적인 절차
• 데이터(재료)가 명사, 연산(행동)이 동사로 표현된 레시피

프로그램 정의

• 자료구조 + 알고리즘
• 레시피를 활용해 완성한 딸기 무스 케이크

---

1-3 알고리즘의 성능 평가 방법

성능 평가 목적

• 얼마나 효율적으로, 빠르게 데이터를 처리하는 지 알기 위해서
• 서로 다른 알고리즘을 평가하기 위해서

성능 평가 방법

• 시간 복잡도: 알고리즘의 수행시간으로, 효율성과 반비례
• 공간 복잡도: 알고리즘이 사용하는 메모리 사용량으로, 효율성과 반비례

입력 데이터의 경우

• 알고리즘에 따라 최악/최상/평균의 경우가 상대적으로 결정된다.
• 데이터의 수는 같고, 위치에 따라 최악/최상/평균의 경우가 결정된다.
• 최악의 경우를 상정하고 시간 복잡도를 측정한다.
  - 이유: 최대 시간을 보장함으로써 신뢰성을 확보하기 위해

실제 측정 시간 V.S. 수학적 계산 시간

• 실제 측정 시간을 성능 평가에 사용하지 않는다.
  - 이유: 실제 측정 시간은 컴퓨터의 성능 등 외적 요인 영향 받음

성능 평가 표기법

• 빅-오 표기법
  - 정의: 모든 N>=N0에 대해서 f(N) <=Cg(N)이 성립하는 양의 상수 C, N0가 존재하면 f(N) <= O(N)이다.
  • 의미: N0 이상의 모든 N에 대해 f(N)이 g(N)보다 크지 않다. (g(N)은 f(N)의 상한이다.)
  • 규칙: 최고차항의 계수 제외 항만 적어준다.(상수항, 최고차항 이하의 차수의 항은 무시한다.)
  • 규칙2: 정의를 만족하는 가장 차수가 낮은 함수를 선택하는 것이 바람직함.
• 빅-오메가 표기법
  - 정의: 모든 N <= N0에 대해서 f(N) >= Cg(N)이 성립하는 양의 상수 C, N0가 존재하면 f(N) >= Ω(N)이다.
  • 의미: N0 이상의 모든 N에 대해 f(N)이 g(N)보다 작지 않다.(g(N)은 f(N)의 하한이다.)
• 빅-세타 표기법
  - 정의: 모든 N >= N0에 대해서 C1g(N) >= f(N) >= C2g(N)이 성립하는 양의 상수 C1, C2, N0가 존재하면, f(N)= Θ(g(N))이다.
  • 의미:Θ(g(N))은 g(N), f(N)과 유사한 증가율을 가지고 있다.

예제: 다음 문제의 시간 복잡도를 구하시오.

Q1.

a = 1
b = 2
c = a + b
print(c)

A1.

시간 복잡도: O(1)

풀이: 입력이 없기 때문, 바뀔 게 없다!
100번 실행시켜도 그 입력이 코드의 시간 복잡도에 영향을 안 주기 때문
항상 네 줄이 실행되고 끝난다.

Q2.

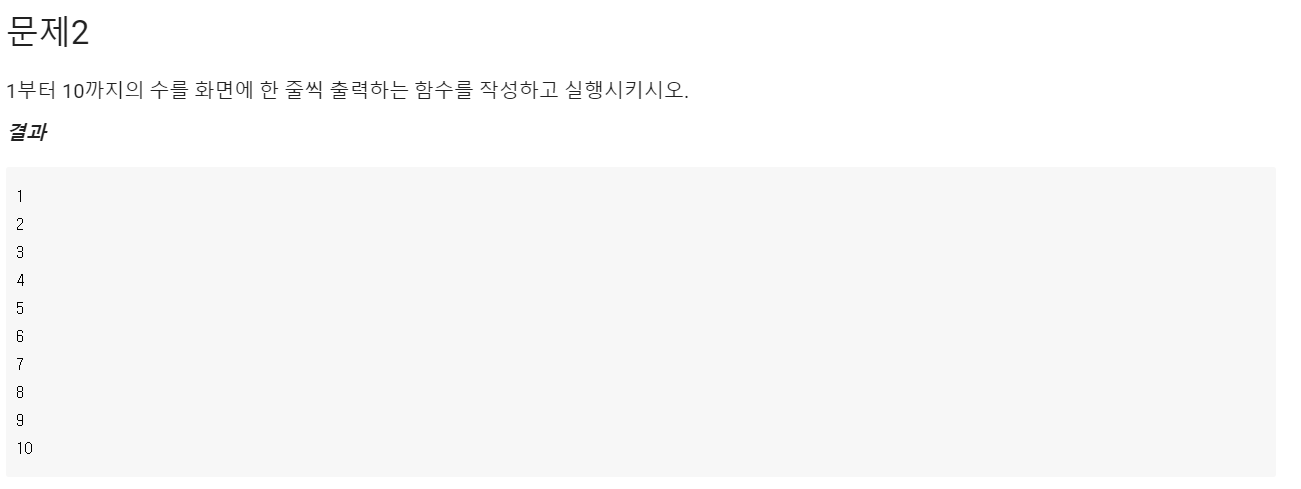
for i in range(1,11):
  print(i)

A2.

시간 복잡도: O(1)
풀이: 입력 받은 데이터가 없기 때문

Q3.

def my_sum(num1, num2):
  return num1 + num2 # 함수 호출이 되면 이 곳으로 return 돌아온다는 뜻.

## 아래는 수정하지 마시오.
print(my_sum(3, 4))  # 함수 my_sum 가 호출됨
print(my_sum(1, 2))

A3.

시간 복잡도: O(1)

풀이: 입력 값에 따라 연산 횟수가 달라지지 않기 때문.

Q4.

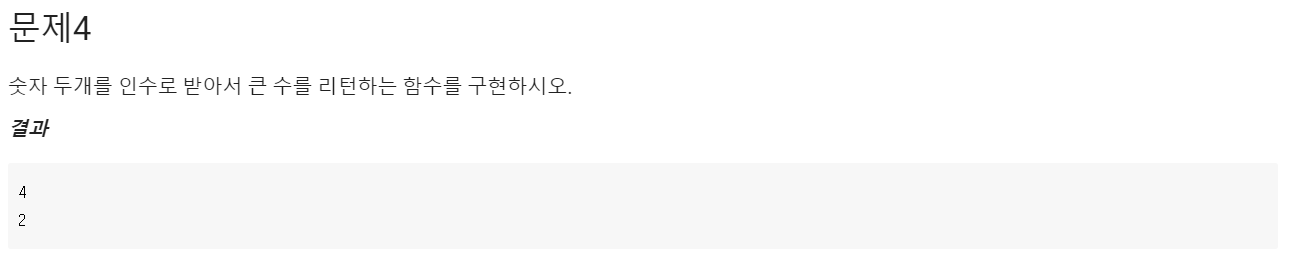
def my_fun2(a, b):
    if a >= b:
      return a
    else:
      return b

## 아래는 수정하지 마시오.
print(my_fun2(4, 3))
print(my_fun2(1, 2))

A4.

시간 복잡도: O(1)

풀이: 둘 중에 하나만 return을 하게 되는데 서로 영향을 주지 않는다. a를 return하거나 b를 return하거나 한 번 return하는 것이다.

Q5.

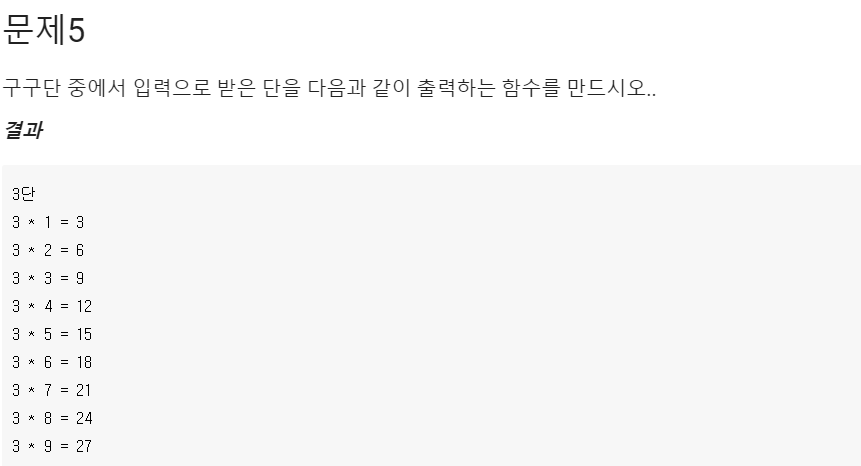
def my_gugu(n):
  print(n, '단')
  for i in range(1,10):
    print(n, ' * ', i, ' = ', n * i)
  print('\n')

## 아래는 수정하지 마시오.
my_gugu(3)

A5.

시간 복잡도: O(1)

풀이: 입력 값과 연산 회수가 상관이 없기 때문이다. 입력값에 따라 연산 회수가 바뀌지 않는다.

Q6.

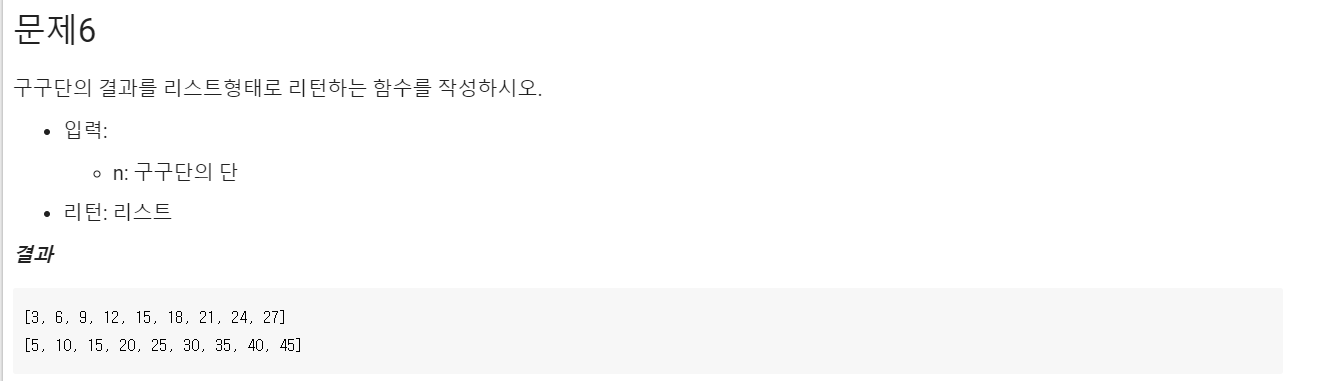
def my_gugu2(n):
  r = [] # 자료형부터 변수에 선언해준다. 자료 구조를 먼저 생각해야 한다.
  for i in range(1,10): # 그 다음이 알고리즘이다.
    r.append(n*i)
  return r

## 아래는 수정하지 마시오.
print(my_gugu2(3)) # 3단의 결과 리턴
print(my_gugu2(5)) # 5단의 결과 리턴

linear comprehension을 이용한 코드 풀이:

def my_gugu2(n):
  return [i*n for i in range(1,10)]

## 아래는 수정하지 마시오.
print(my_gugu2(3)) # 3단의 결과 리턴
print(my_gugu2(5)) # 5단의 결과 리턴

A6.

시간 복잡도: O(1)
풀이: 입력값에 따라 연산 횟수가 바뀌지 않는다.