$O(n)$ 복잡도 [완전탐색]

약수의 개수는 1에서부 n까지의 모든 수를 돌며 n이 나누어 떨어지는지 확인하고 개수를 올리면 된다.

function find_divisor_count(n) {
  let count = 0;
  
  for (let i = 1; i <= n; i++) {
    if (n % i === 0) count++;  
  }
  
  return count;
}

작은 수일 경우 문제가 되지 않지만 숫자가 커져도 n을 모두 돌기 때문에 시간 복잡도는 O(n)이다.

$O(\sqrt{n})$ 복잡도

n의 약수 중 하나를 m이라고 했을때 다른 약수는 n/m이 된다.
n=10 이고 약수 하나가 2라면 10/2 = 5 도 약수이다.
따라서 약수 m을 하나 구한다면 2개의 약수를 찾은거나 다름이 없다

또한 n이 어떤 수의 제곱인 경우 제곱근은 하나만 구하면 된다.
n = 100인 경우 10만 구하면 끝.

그럼 몇번만에 약수를 찾아낼 수 있을까?

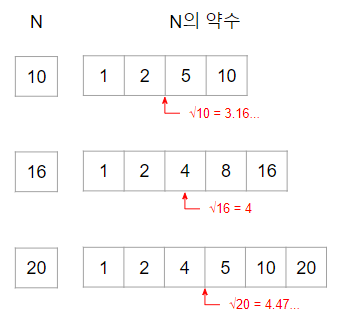
그림에 따르면 $\sqrt{n}$까지 돌면 모든 약수의 개수를 찾을 수 있다.

위의 모든 것을 조합하여 코딩을 짜면 아래와 같다

function find_divisor_count(n) {
  let count = 0;
  
  for (let i = 1; i * i <= n; i++) {
    if (i * i === n) count++;
    else if (n % i === 0) count += 2;
  }
  
  return count;
}

이제 $O(\sqrt{n})$의 복잡도로 약수의 개수를 금방 구할 수 있다

참고 : 모든 약수를 구하는 알고리즘은 O(sqrt(n))이다

마치며...

이제는 알고리즘의 문제를 푸는 것보다 시간초과에서 많이 실패하는 일이 늘어나고 있어서 평소에 쉽던 문제들도 시간 복잡도를 줄일 수 있는 방법을 찾아나가야 할 것 같다.

+) 해당 방법을 사용할 수 있는 문제