Heap Sort

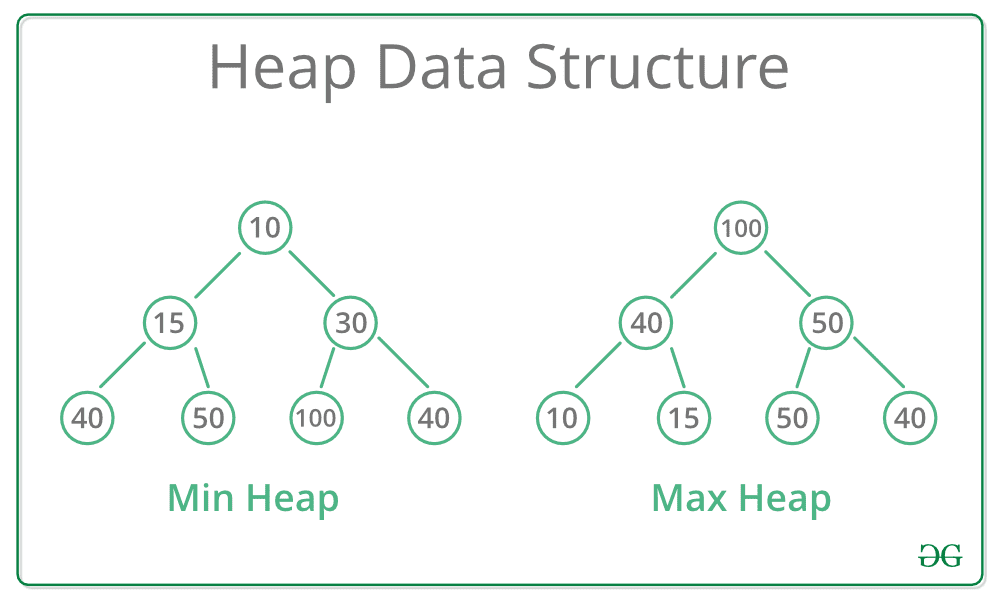
힙(Heap)에는 최대힙(Max heap), 최소힙(Min heap) 두 종류가 있다.

• 최대 힙: 부모 노드는 항상 자식 노드보다 크거나 같아야 한다.
• 최소 힙: 부모 노드는 항상 자식 노드보다 값이 작아야 한다.

즉, 최대 힙의 루트는 힙 내에서 가장 큰 값, 최소 힙의 루트는 힙 내에서 가장 작은 값을 의미한다는 것이다.
힙 전체를 통틀어서 이 규칙이 꼭 유지되어야 한다.
최대 힙과 최소 힙의 차이는 사실 정렬할 때 조건 밖에 없다.

우선순위 큐와 연관지어 Min Heap 을 구현해보자.

일반적으로 힙 자료구조는 이진 트리로 구현한다.
이진 트리는 각각의 부모 노드가 오로지 두 개의 자식 노드(left, right)만 가질 수 있는 트리를 의미한다.
추가적으로 힙은 완전 이진 트리의 구조를 사용하는데, 트리의 가장 아래 층을 제외하고는 상단의 모든 레벨이 완전히 채워져야 한다.

따라서, MIN HEAP은

1. 부모 노드는 항상 자식 노드보다 값이 작아야 한다.
2. 한 레벨이 모두 채워져야 다음 레벨로 트리가 늘어날 수 있다.

이 두 가지 규칙을 지키는 자료구조이다.
그리고 이진 트리 자료구조 임에도 배열로 구현할 수 있다.

배열을 정렬하기 위해 먼저 계속 배열의 요소들을 insert해서 최소 힙을 만든 후에 최소 힙의 루트 노드를 계속 pop하면 오름차순으로 정렬된 배열을 얻을 수 있다.

위와 같은 트리를 아래와 같은 배열로 나타낼 수 있다.
이렇게 하면 이진트리를 평평하게 배열에 담을 수 있다.

index: 0 1 2 3 4 5
value: 1 4 8 5 2 3

Min Heap 구현하기

// 최소 힙 구현
function swap(idx1, idx2, arr) {
	[arr[idx1], arr[idx2]] = [arr[idx2], arr[idx1]];
}

// heap내에서 parentIdx를 구하는 모듈
function getParentIdx(idx) {
	return Math.floor((idx - 1) / 2);
}

// heap 삽입 구현
function insert(heap, item) {
	heap.push(item);
	if (heap.length > 1) {
		let curIdx = heap.length - 1;
		let parentIdx = getParentIdx(curIdx);
		while (parentIdx >= 0 && heap[curIdx] < heap[parentIdx]) {
			// 최대 힙과 부등호만 반대
			swap(curIdx, parentIdx, heap);
			curIdx = parentIdx;
			parentIdx = getParentIdx(curIdx);
		}
	}
	return heap;
}

// heap 삭제 구현
// 항상 rootNode(최솟값)가 삭제되며 제일 끝 인덱스가 rootNode 자리에 오르게 되고,
// 자식 노드들과 반복 비교를 진행해서,
// 최종적으로 삭제되었던 rootNode의 다음 최솟값이 rootNode 자리에 오른다
function removeRoot(heap) {
	// 배열의 첫번째(최소값)과 배열의 마지막 값을 바꾼다.
	swap(0, heap.length - 1, heap);
	// 배열의 최소값 제거
	heap.pop();

	if (heap.length === 0) return [];

	// 다시 최소힙을 유지
	let curIdx;
	let minIdx = 0;
	while (curIdx !== minIdx) {
		curIdx = minIdx;
		let leftChild = curIdx * 2 + 1;
		let rightChild = curIdx * 2 + 2;
		if (leftChild < heap.length && heap[leftChild] < heap[minIdx]) {
			minIdx = leftChild;
		}

		if (rightChild < heap.length && heap[rightChild] < heap[minIdx]) {
			minIdx = rightChild;
		}

		swap(curIdx, minIdx, heap);
	}

	return heap;
}

const binaryHeap = function (arr) {
	return arr.reduce((heap, item) => {
		return insert(heap, item);
	}, []);
};

// heapSort 구현
// removeRoot(heap)을 진행하면 항상 rootNode에는 최솟값이 존재하기 때문에
// heap이 빈 배열이 될 때까지 heap[0]을 result 배열에 넣어준다.
const heapSort = function (arr) {
	let minHeap = binaryHeap(arr);
	// TODO: 여기에 코드를 작성합니다.
	const result = [];
	while (minHeap.length > 0) {
		result.push(minHeap[0]);
		minHeap = removeRoot(minHeap);
	}
	return result;
};