TIMESTAMP
@200919 시작~4.1
@200920 4.2~
@200922 완료
들어가기 전에
- 머신러닝 알고리즘은 보통 많은 양의 수치 계산이 필요하다. 정답을 구하기 위해 수식으로 유도하는 것이 아니라, 반복적인 과정을 통해 솔루션의 추정치를 업데이트하는 방식으로 수학적인 문제를 해결하는 알고리즘이다.
- 일반적으로 최적화(함수를 최소화하거나 최대화하는 값 찾기)와 선형 연립방정식을 푸는 과정이 포함된다.
- 함수에 실수(real numbers)를 포함하는 경우 디지털 컴퓨터에서 수학적인 함수를 평가하는 것조차 어려줄 수 있다. 유한한 양의 메모리를 사용하기 때문에 실수를 정확하게 표현할 수 없기 때문이다.
- 한정된 숫자의 비트에서 알고리즘이 여전히 작동할까?
- 알고리즘은 보통 실수(real numbers)로 지정되지만, 유한의(finite) 컴퓨터에서는 실수를 구현할 수 없다.
- 입력값의 작은 변화가 출력값에서 큰 변화를 일으킬까?
- 반올림 오류, 노이즈, 측정 오류로 인해 큰 변화가 발생할 수 있다.
- 최상의 입력값을 위한 Iterative search는 어렵다.
Roadmap
- Iterative Optimization
- Gradient descent
- Curvature
- Constrained optimization
- Rounding error, underflow, overflow
Overflow and Underflow
Numerical concerns for implementations of deep learning algorithms
- 디지털 컴퓨터에서 연속수학(continuous math)를 수행하는 데 있어 유한한 수의 비트 패턴으로 무한히 많은 실수를 표현해야 한다는 점은 근본적인 어려움이다. 컴퓨터로 거의 모든 실수에서 숫자로 나타날 때 근사 오류가 발생하며, 대부분의 경우 단순히 반올림 오류이다.
- 반올림 오류는 특히 여러 연산에서 복합이 될 때 문제가 되고, 반올림 오류를 최소화하도록 설계되지 않은 경우에는 이론적으로 작동하는 알고리즘이 실패할 수 있다.
- 언더플로우(underflow)
- 언더플로우는 0 근처의 숫자가 0으로 반올림될 때 발생한다. 많은 함수들은 인수(argument)가 아주 작은 양수대신 0일 때 정성적으로 다르게 작동한다. (예를 들어, 0으로 나누거나 0에 대해 로그를 취하는 것)
- 오버플로우(overflow)
- 오버플로우는 매우 큰 숫자가 나 로 근사될 때 발생하는 것으로, 추가적인 연산이 될 경우 not-a-number 값으로 변하게 된다.
- 언더플로우와 오버플로우를 반드시 안정화 해야하는 함수 중 하나는 softmax이다. softmax는 주로 다항분포와 관련된 확률을 예측할 때 사용된다.
- 모든 가 상수 라고 한다면, 모든 결과값은 이 될 것이다. 만약 가 매우 크다면 이는 일어나지 않는 것이다.
- c가 매우 음수라면(very negative), 는 언더플로우가 될 것이다. 즉 분모가 0이 되어 최종 결과는 undefined이다.
- c가 매우 큰 양수라면, 는 오버플로우이고, 이 또한 undefined가 된다.
- 두 경우 모두 로 해결이 가능하다. ()
- 입력 벡터에 스칼라를 더하거나 빼도 softmax 함수의 값은 변하지 않는다.
- 를 빼는 것은 에 들어가는 가장 큰 인수(argument)를 0으로 만들어, 오버플로우의 가능성을 없앤다.
- 이와 같이, 분모의 적어도 한 항은 1이 되기 때문에, 0에 의해 나눠지는 언더플로우의 가능성 또한 배제하게 된다.
- 여전히 작은 문제가 존재한다. 여전히 분자의 언더플로우는 식을 0으로 만들 수 있어, 를 취하면 계속해서 잘못된 값을 가지게 된다. 그 대신에 반드시 분리된 함수를 실행하여 수학적으로 안정적인 방향으로 을 계산해야 하고, 에 행했던 동일한 방식으로 를 안정화시킬 수 있다.
- 책에 설명된 다양한 알고리즘을 구현하는 데 관련된 모든 수치적 고려사항을 명시적으로 설명하지는 않았다. 로우레벨 라이브러리 개발자는 딥러닝 알고리즘을 구현할 때 이 문제를 염두에 두어야 한다.
Poor Conditioning
Condition Number
- Conditioning은 입력값의 작은 변화에 대해서 함수가 얼마나 빠르게 변하는지를 나타내는 것이다.
- 입력이 약간 변할 때마다 함수가 빠르게 변한다면 입력값의 반올림 오류는 출력값의 큰 변화를 초래할 수 있기 때문에 문제가 될 수 있다.
- 함수 에 대해서 가 고유값 분해를 가질 때, 조건수(condition number)는 다음과 같다.
- 최대고유값과 최소고유값의 비로, 만약 조건수가 크다면 역행렬은 입력값의 오류에 대해 특히 예민하다. 이러한 민감성은 역행렬 과정에서의 반올림 문제가 아니라 행렬 자체의 내재된 특성이다. 역행렬로 인해서 poor conditioned matrix의 내재되었던 오류 가능성을 증대시킨다. 실제로는 역행렬 자체의 수치적인 오류에 의해서 이러한 오류가 더욱 가중된다.
Gradient-Based Optimization
Gradient Descent
- 대부분의 딥러닝 알고리즘은 일종의 최적화를 포함한다. 최적화는 를 바꾸면서 함수 를 최소화하거나 최대화하는 과정이다. 일반적으로는 를 최소화하는 것을 최적화라고 하며, 최대화는 를 최소화하면 된다.
- 우리가 최소화하거나 최대화하고 싶은 함수를 목적함수(objective function)이나 criterion이라고 한다. 만약 최소화하는 경우에는 비용함수(cost function), 손실함수(loss function) 혹은 error function이라고 한다.
- 함수를 최소화하거나 최대화하는 값을 *와 함께 표현한다. (예: )
- 이미 미적분을 알고 있을 것이라고 가정하지만, 미적분이 최적화와 어떻게 관련되는지를 다음으로 요약하여 설명한다.
- 와 가 모두 실수인 함수가 있을 때, 함수의 미분(derivative)는 혹은 이며,점 에서의 의 기울기를 의미한다. 다시 말해, 입력값이 조금씩 달라질 때마다 대응되는 결과값의 변화를 정량화한 것이다 :
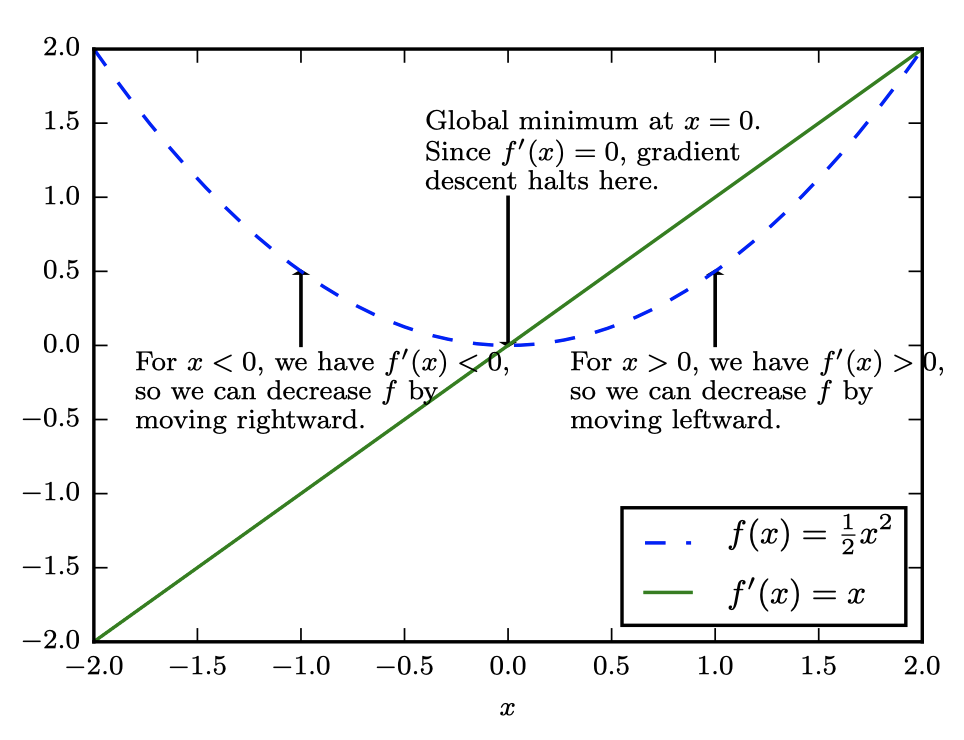
- 따라서 미분은 를 변화시키기 위해 를 얼마나 움직여야하는지 알려주기 때문에 함수를 최소화시키는 데 유용하다.
- 예를 들어, 아주 작은 값일 때 는 보다 작다. 따라서 미분의 반대 방향으로 를 움직여 를 감소시킬 수 있다. 이러한 방식을 gradient descent라고 한다.
Critical Points
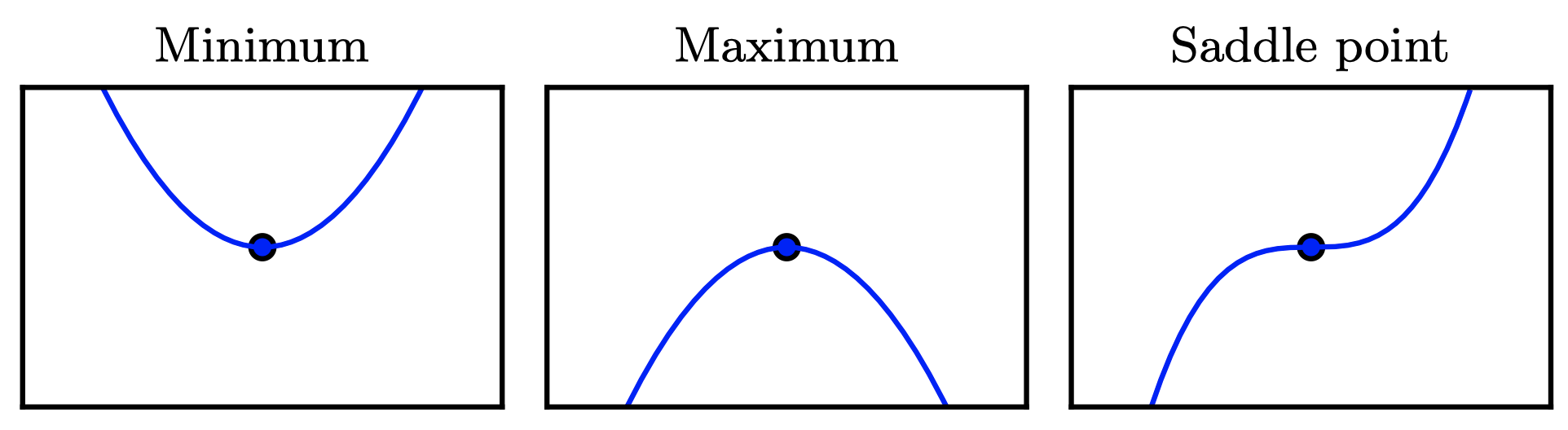
- 일 때, 미분은 어느 방향으로 갈지 아무 정보를 제공하지 않는다. 이 되는 지점을 critical points 혹은 stationary points라고 한다.
- Local minimum은 가 다른 근접 점들보다 작을 때를 말하며 더 이상 를 감소시킬 수가 없다.
- Local maximum은 가 다른 근접 점들보다 클 때를 말하며 더 이상 를 증가시킬 수가 없다.
- maxima도 minima도 아닌 것 critical points를 saddle points라고 한다.
Approximate Optimization
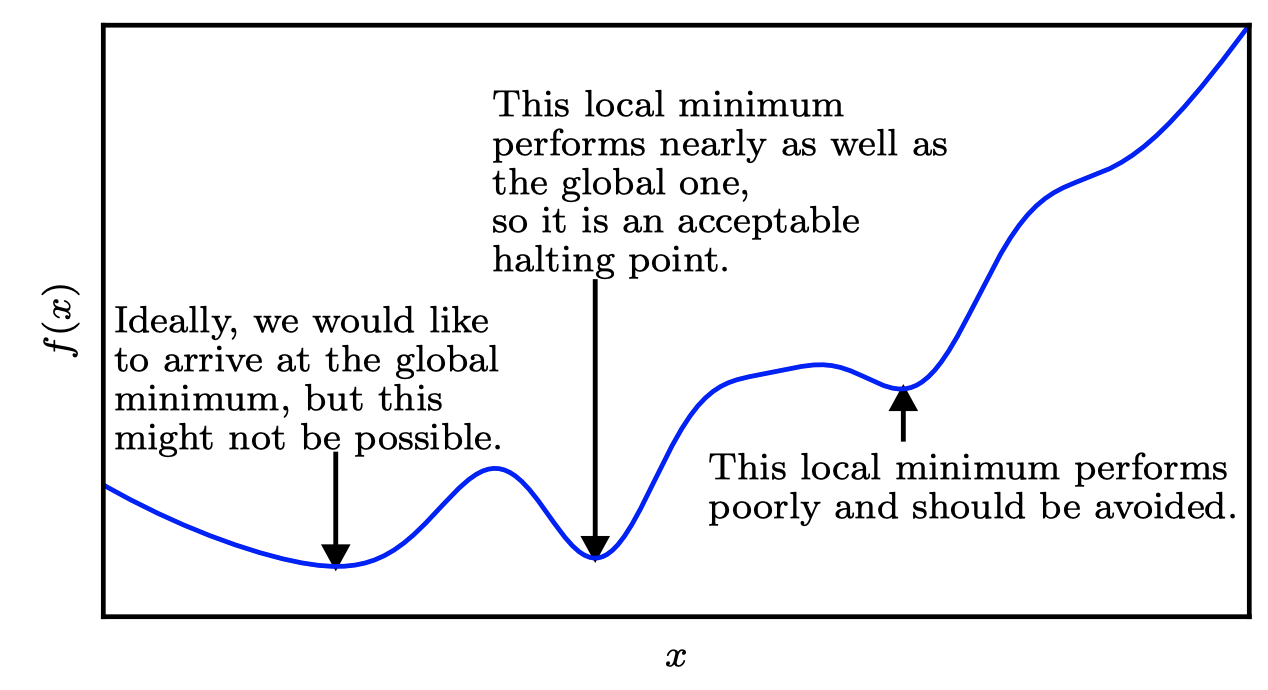
- 의 최저값을 얻는 점은 global minimum이며, 오직 하나가 될 수도 있고 여러개가 될 수도 있다. 또한 globally optimal하지 않은 local minima가 존재할 수 있다. 딥러닝에서는 local minima와 saddle points가 많은 함수를 최적화하기 때문에, 입력값이 특히 다차원일 때 최적화가 어렵다. 따라서 가 매우 낮은 지점에서 보통 만족을 하지만, 이것이 꼭 최소값이지는 않는다.
Steepest descent
-
단위 벡터 방향에서의 방향도함수(directional derivative)는 함수 의 방향에서의 기울기다.
- 다시 말해, 방향도함수는 에 대한 함수 의 기울기다(evaluated at ).
- 연쇄법칙(chain rule)에 의해 일 때, 는 가 된다.
-
를 최소화하기 위해서는 가장 빠르게 를 감소시키는 방향을 찾고자 하고, 이때 방향도함수를 사용할 수 있다 (는 와 기울기 사이의 각도)
- 로 치환하고 와 관련되지 않은 항을 무시한다면, 위의 식은 가 되고, 가 기울기와 반대 방향이 될 때 최소화된다.
- 다시 말해, 기울기의 점들은 윗 방향을 향하고, 기울기의 음수 점들은 아랫 방향을 향한다. 기울기 음수 방향으로 움직인다면 를 감소시킬 수 있다. 이를 method of steepest descent 혹은 gradient descent라고 한다.
-
Steepest descent는 아래와 같은 새로운 지점을 제시한다.
- 은 학습률(learning rate)로, 다음 스텝의 크기를 결정하는 양수의 스칼라이다.
- 은 다양한 방법으로 선택할 수 있으며,
- 보통 작은 상수로 지정한다.
(Sometimes, we can solve for the step size that makes the directional derivative vanish.) - 또 다른 방법은 line search로, 여러 에 대해 를 평가하고 가장 작은 목적함수 값을 만드는 것을 선택할 수 있다.
- 보통 작은 상수로 지정한다.
-
Steepest descent는 기울기의 모든 지점이 0이거나 0에 가까울 때 수렴한다. 여러 경우에서는 이러한 반복적인(iterative) 알고리즘을 하지 않고, 에 대해 을 풀어 바로 critical points로 직행할 수 있다.
-
비록 gradient descent는 연속적인 공간에서의 최적화로 국한되어 있지만, 더 나은 곳을 향해 반복해서 조금씩 움직인다는 개념은 이산 공간으로 일반화될 수 있다. 이산적인 파라미터들의 목적함수를 증가시키는 것은 hill climbing이라고 한다.
Jacobian Matrix
- 입력값과 출력값이 모두 벡터인 함수의 모든 편미분을 구해야할 때가 있고, 이러한 형태의 행렬을 야코비안 행렬(Jacobian matrix)이라고 한다.
- 함수 에 대하여 의 야코비안 행렬 은 으로 정의된다
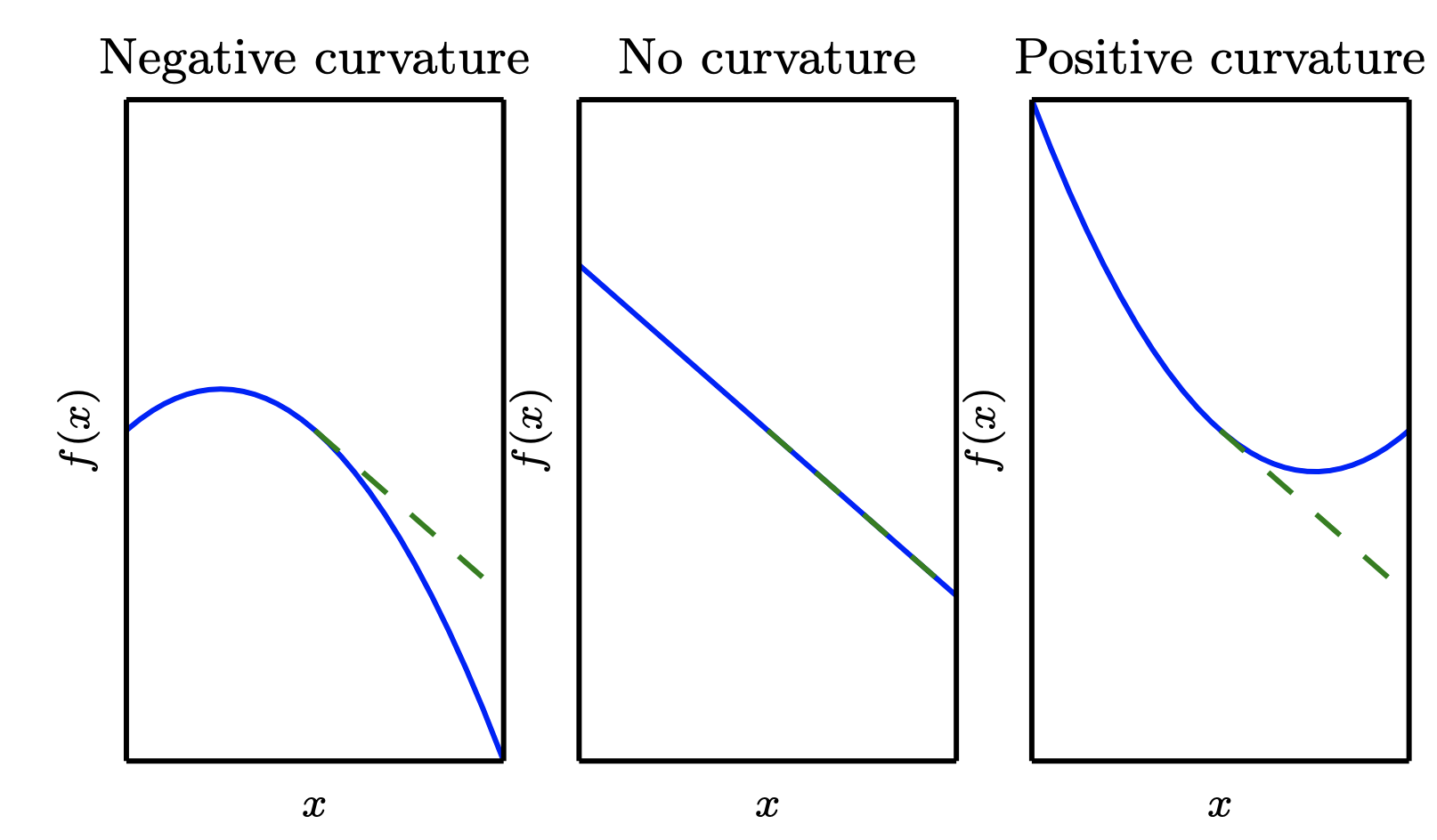
Curvature
-
도함수의 도함수를 구해야할 때가 있고, 이를 이계도함수(second derivative)라고 한다.
- 함수 에 대하여, 에 대한 의 도함수의 에 대한 도함수는 로 표현할 수 있다. 1차원에서는 를 로 표현할 수 있다.
-
이계도함수는 입력값이 달라짐에 따라 도함수가 얼마나 변하는지를 나타내는 것으로, gradient step으로 인해 우리가 기대하는 더 나은 결과가 나올지를 기울기를 기반으로 말해준다.
-
이계도함수는 곡률(curvature)을 측정하는 것으로 생각할 수 있다.
[예시] 이차함수에서의 이계도함수
실제로 많은 함수는 이차함수는 아니지만 국소적으로는 이차함수로 근사할 수 있다
(1) 만약 이계도함수가 0이라면, 곡률이 없고 완전한 직선을 의미한다. 만약 기울기가 1이라면, 기울기의 반대방향으로 크기만큼 이동할 수 있고 이 경우 비용함수는 만큼 감소할 것이다.
(2) 만약 이계도함수가 음수라면, 아래쪽으로 휘어진 형태이므로 비용함수는 보다 크게 감소할 것이다.
(3) 만약 이계도함수가 양수라면, 위쪽으로 휘어진 형태이므로 비용함수는 보다 작게 감소할 것이다.
Hessian Matrix
- 다수의 입력 차원을 가지는 함수는 이계도함수가 여러개이다. 이와 같은 이계도함수의 행렬을 헤세 행렬(Hessian matrix)이라고 하며, 기울기의 야코비안과 같다 ("Hessian is the Jacobian of the gradient")
- 이차편미분이 연속인 모든 곳은 미분의 연산은 교환법칙이 성립된다.이는 곧 이고, 해당 지점에서 헤세 행렬이 대칭이라는 것을 의미한다.
- 딥러닝에서 우리가 마주하는 함수의 대부분은 거의 모든 곳에서 대칭적인 헤세 행렬을 가진다. 따라서 실수의 고유값과 그와 직교하는 고유벡터의 쌍으로 분해할 수 있다.
- 단위 벡터 로 대변되는 특정 방향의 이계도함수는 로 표현할 수 있다.
- 만약 가 의 고유벡터라면, 해당 방향의 이계도함수는 그에 대응되는 고유값이 된다.
- 이외의 의 경우, 이계도함수는 모든 고유값의 가중평균이다. 이때 가중치는 0과 1 사이며, 와의 각도가 작을수록 더 큰 가중치를 받는다.
- 최대고유값은 최대 이계도함수를 결정하며, 최소고유값은 최소 이계도함수를 결정한다.
- 이계도함수는 실행하고자 하는 다음 gradient descept 스텝이 얼마나 잘 작동할지를 말해주는 것으로, 현재 지점 에 대해 를 테일러 이차 근사할 수 있다:(는 gradient, 는 에서의 Hessian)
- 만약 학습률 일 경우, 새로운 는 이고, 이를 위의 근사식에 대입하면 다음과 같다:
- 위 식에는 세가지 항이 존재한다.
- 함수의 원래 값
- 함수의 기울기로 인한 기대되는 개선 정도
- 함수의 곡률을 고려한 보정
- 만약 마지막 항이 너무 크다면, gradient step이 위쪽으로 움직일 것이다.
- 가 0 이하인 경우, 테일러 근사는 를 영원히 증가시키는 것은 를 영원히 감소시킬 것이라고 예측한다. 실제로 테일러 급수는 크기가 큰 에 대해서는 정확하지 않으며, 따라서 이런 경우 더 많은 휴리스틱 선택에 의존해야 한다.
- 가 양수인 경우, 함수의 테일러 근사를 감소시키는 최적의 스텝 사이즈는 많은 경우에 다음과 같다:
- 최악의 경우, 가 최대고유값 에 대응되는 의 고유벡터와 평행하다면, 최적의 스텝 사이즈는 이다.
- 최소화하고자 하는 함수가 2차함수에 의해 잘 근사되는 한, 헤세 행렬의 고유값이 학습률의 크기를 결정한다.
- 이계도함수 critical point가 local maximum, local minimum, saddle point를 결정하는데 사용될 수 있다.
- critical point에서 이다. 이라면 는 오른쪽으로 갈 때 증가하고 왼쪽으로 갈때 감소한다. 충분히 작은 에서 과 을 의미한다. 다시 말해, 오른쪽으로 갈 때 기울기는 오른쪽으로 윗 방향을 향하고, 왼쪽으로 갈 때 기울기는 왼쪽으로 아래 방향을 향한다.
- 그러므로 이라면 는 local minimum이다.
- 이와 비슷하게 이라면 local maximum이다.
- 이를 second derivative test라고 한다. 일 경우에는 결론지을 수 없으며, 이 경우 는 saddle point이나 flat region의 일부일 수 있다.
- critical point에서 이다. 이라면 는 오른쪽으로 갈 때 증가하고 왼쪽으로 갈때 감소한다. 충분히 작은 에서 과 을 의미한다. 다시 말해, 오른쪽으로 갈 때 기울기는 오른쪽으로 윗 방향을 향하고, 왼쪽으로 갈 때 기울기는 왼쪽으로 아래 방향을 향한다.
Second derivative test
- 다차원에서는 함수의 모든 이계도함수를 확인해야 한다. 헤세 행렬의 고유값분해를 통해 second derivative test를 여러 차원으로 일반화할 수 있다.
- 인 Critical point에서 해당 점이 local maximum, local minimum, saddle point인지 결정하기 위해 헤세 행렬의 고유값을 확인할 수 있다.
- 헤세 행렬의 모든 고유값이 양수(positive definite)일 경우 해당 점은 local minimum이다. 이는 모든 방향의 이계도함수가 양수여야 하고, second derivative test를 참조하여 확인할 수 있다.
- 마찬가지로 헤세 행렬의 모든 고유값이 음수(negative definite)라면 해당 점은 local maximum이다. 다차원에서 실제로 경우에 따라 saddle point의 증거를 찾을 수 있다. 적어도 하나의 고유값이 양수이고 적어도 하나가 음수라면, 는 의 한 단면에서는 local maximum이지만 다른 단면에서는 local minimum이다.
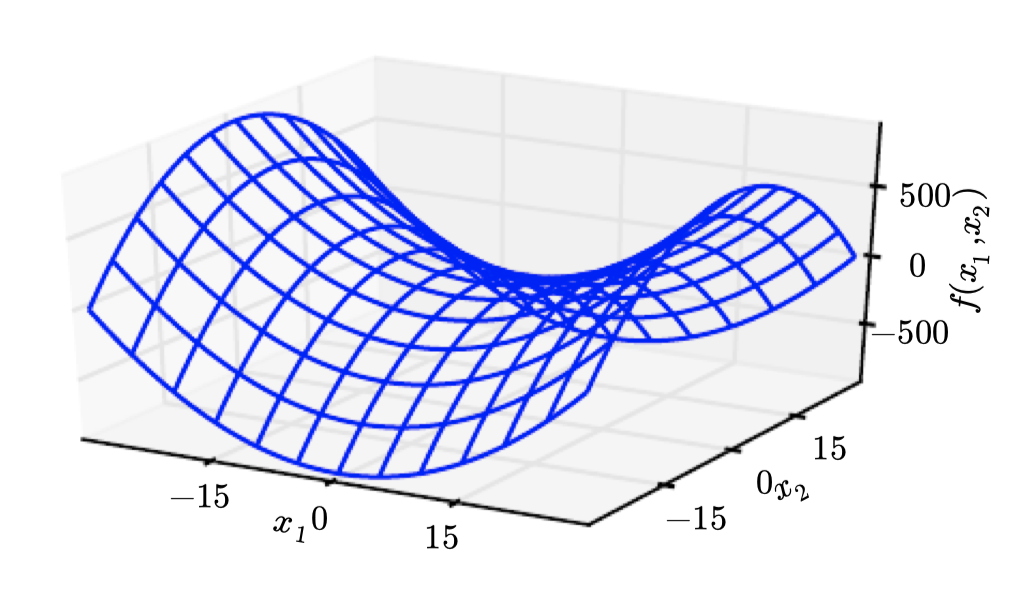
- 마지막으로 다차원 second derivative test도 단변량 경우와 같이 결론을 내지 못할 수 있다. 0이 아닌 고유값이 동일한 부호지만 하나 이상의 고유값이 0이라면 결론 지을 수 없다.
Newton's method
-
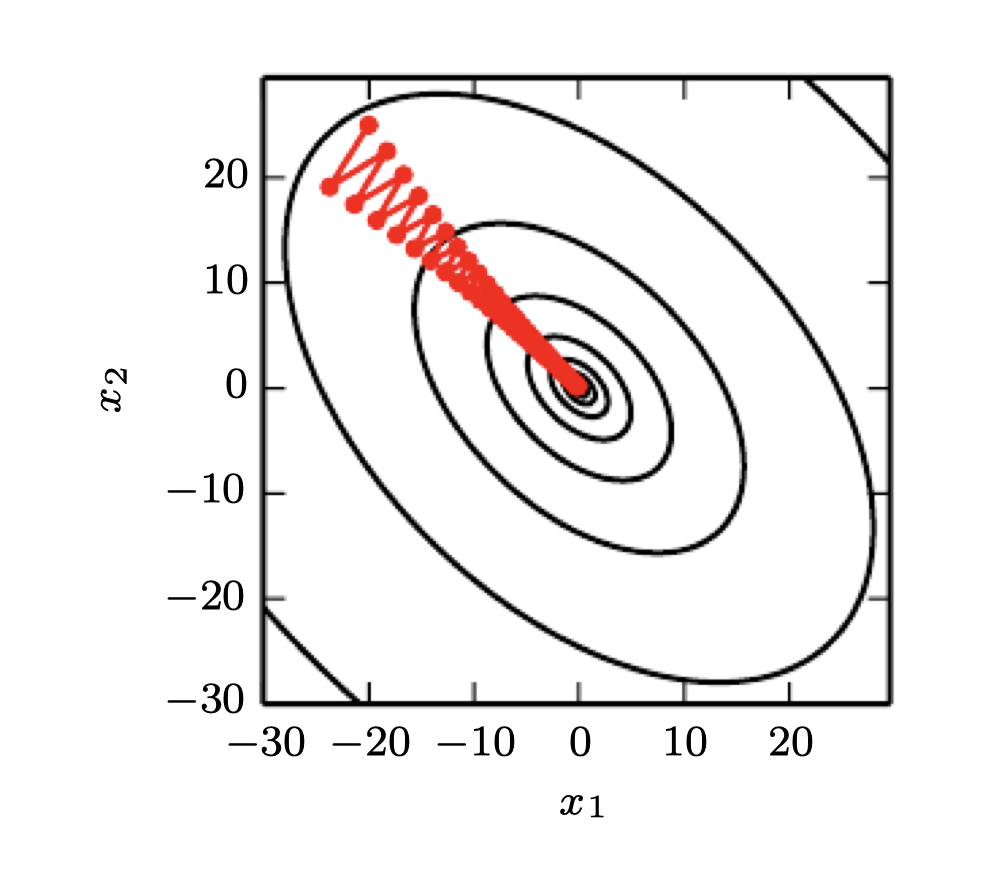
다차원에서는 한 지점에서 각 방향에 대해 서로 다른 이계도함수가 있다. 이 점의 헤세 행렬의 조건수는 서로 이계도함수가 얼마나 다른지를 측정한다. 헤세 행렬이 poor condition numer을 가질때, gradient descent는 제대로 수행되지 않는다. 이는 한 방향에서는 미분이 빠르게 증가하고 다른 방향에서는 느리게 증가하기 때문이다. Gradient descent는 이러한 미분의 변화를 인지하지 못하기 때문에 미분이 더 오랫동안 음수로 유지되는 방향을 우선적으로 탐색해야한다는 것을 모른다. 또한 적절한 스텝 사이즈를 선택하기가 어렵다. 스텝 사이즈는 최소값을 오버슈팅하거나 양의 곡률이 강한 방향으로 오르지 않도록 충분히 작아야 한다. 이는 보통 스텝 사이즈가 너무 작아서 곡률이 작은 다른 방향으로 상당한 진전을 이루지 못하는 것을 의미한다.
-
헤세 행렬의 정보로부터 이러한 이슈를 해결할 수 있다. 가장 간단한 방법은 뉴턴의 방법(Newton's method)이다. 뉴턴의 방법은 2차 테일러 급수를 사용하여 근처의 를 근사한다.
이 함수의 critical point에 대해 풀어보면:
- 가 positive definite quadratic이라면, 뉴턴의 방법은 위의 식을 한 번 적용하여 함수의 최소값으로 직접 가게 된다.
- 만약 가 실제로는 아니지만 국소적으로는 positive definite quadratic이라면 위의 뉴턴의 방법을 여러 번 적용할 수 있다.
-
근사치를 반복적으로 업데이트하고 근사치의 최소값으로 점프하면 gradient descent보다 critical point로 더 빠르게 도달할 수 있다. 이는 local minimum 근처에서 유용하지만 saddle point 근처에서는 위험하다. 뉴턴의 방법은 근처 critical point가 최소인 경우(헤세 행렬의 모든 고유값이 양수)에만 적절하지만, gradient descent는 saddle points로 끌려가지는 않는다.
Lipschitz continuous
- gradient descent처럼 gradient만을 이용하는 최적화 알고리즘을 first-order optimization algorithms라고 부른다.
- 뉴턴의 방법과 같이 헤세 행렬도 사용하는 최적화 알고리즘을 second-order optimization algorithms이라고 한다.
-
이 책의 대부분의 최적화 알고리즘은 다양한 함수에 적용할 수 있지만 보장할 수는 없다. 딥러닝에 사용되는 함수는 꽤 복잡하기 때문에 딥러닝 알고리즘은 확신을 할 수 없는 경향이 있다. 다른 많은 분야에서 최적화에 대한 지배적인 접근 방식은 제한된 함수군에 대한 최적화 알고리즘을 설계하는 것이다.
-
딥러닝의 맥락에서는 립시츠 연속(Lipschitz continuous)이거나 립시츠 연속 도함수를 가지는 것으로 제한할 때 몇 개의 보장을 할 수 있다. 립시츠 연속 함수는 변화율이 립시츠 상수 (Lipschitz constant)로 바운드된 함수 이다.
-
이 속성은 gradient descent와 같은 알고리즘에 의한 입력값의 작은 변화가 출력값의 작은 변화를 가질 것이라는 가정을 정량화할 수 있기 때문에 유용하다. 립시츠 연속성도 상당히 약간 제약 조건이며, 딥러닝의 많은 최적화 문제는 비교적 작은 변경으로 립시츠를 연속적으로 만들 수 있다.
Convex optimization
- 아마도 가장 성공적인 특화된 최적화 분야는 컨벡스 최적화(convex optimization)이다. 컨벡스 최적화 알고리즘은 더 강력한 제한을 만들어 많은 보장을 제공할 수 있다. 컨벡스 최적화 알고리즘은 컨벡스 함수(헤세 행렬이 모든 곳에서 positive semidefinite)에만 적용할 수 있다. 이러한 함수는 saddle point가 없고 모든 local minima가 반드시 global minima이기 때문에 잘 작동한다. 그러나 딥러닝의 대부분의 문제는 컨벡스 최적화의 측면에서 표현하기가 어렵다. 컨벡스 최적화는 일부 딥러닝 알고리즘의 서브 루틴으로만 사용된다. 컨벡스 최적화의 분석에서 얻은 아이디어는 딥러닝 알고리즘의 수렴을 증명하는데 유용할 수 있다. 하지만 일반적으로 컨벡스 최적화의 중요성은 딥러닝의 맥락에서 크게 감소한다.
Constraint Optimization
-
때로는 우리는 가능한 모든 값 외에도 어떤 집합 에서 값들에 대해 의 최대/최소값을 구하고자할 때가 있으며, 이를 contrained optimization이라고 한다. 집합 내에 있는 점 을 feasible points라고 한다.
-
가장 일반적인 접근 방식은 과 같은 norm 제약을 가하는 것이다.
-
contrained optimization의 하나의 간단한 접근 방식은 제약 조건을 고려하여 gradient descent를 수정하는 것이다. 스텝 사이즈로 작은 크기의 상수 를 사용한다면, gradient descent를 수행할 수 있고, 이 결과를 다시 로 넣는다.
Karush-Kuhn-Tucker
-
Karush-Kuhn-Tucker (KKT) 접근 방식은 매우 일반적인 솔루션을 제공한다. KKT 접근을 통해 generalized Lagrangian 혹은 generalized Lagrange function이라는 함수를 도입할 수 있다.
-
Lagrangian을 정의하기 위해, equations와 inequalities의 측면에서 를 표현해야 한다. 을 개의 함수 와 개의 함수 의 측면에서 표현하여, { and }이 되도록 한다.
-
와 관련된 equations들을 equality constraints라고 하고 와 관련된 inequalities를 inequality constraints라고 한다.
-
각 제약에 KKT multipliers인 새로운 변수 와 를 도입하면, generalized Lagrangian은 다음과 같다: